Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T17:49:18.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurement of local mechanical properties using multiple indentations by a special conical indenter and error analysis

Published online by Cambridge University Press:  06 January 2016

Shigeru Hamada ,
Shogo Kashiwa  and
Hiroshi Noguchi
Shigeru Hamada
Affiliation:
Department of Mechanical Engineering, Faculty of Engineering, Kyushu University, Fukuoka 819-0395, Japan
Shogo Kashiwa
Affiliation:
Department of Mechanical Engineering, Graduate School of Engineering, Kyushu University, Fukuoka 819-0395, Japan
Hiroshi Noguchi*
Affiliation:
Department of Mechanical Engineering, Faculty of Engineering, Kyushu University, Fukuoka 819-0395, Japan
*
a) Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

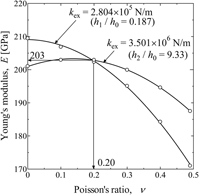
This paper proposes a method for determining the mechanical properties (Young's modulus, Poisson's ratio, yield strength, and work hardening factor) of a material at a specific point using an indentation technique that utilizes a specially designed indenter in conjunction with an inverse problem and finite element analyses. The specially designed indenter combines the characteristics of spherical and conical indenters and can be used to produce multiple indentations at a single point. The feasibility of the proposed method for determining the local mechanical properties of a material was confirmed by detailed precision verifications in the ideal case and the worst case.

Keywords

mechanical propertiesindentationinverse problemFEM analysis
Type
Articles
Information
Journal of Materials Research , Volume 31 , Issue 2 , 28 January 2016 , pp. 259 - 273
Copyright
Copyright © Materials Research Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Sinclar, G.M.: An investigation of the coaxing effect in fatigue of metals. Proc., Am. Soc. Test. Mater. 52, 743 (1952).Google Scholar
Lipsitt, H.A. and Home, G.T.: The fatigue behavior of decarburized steels. Proc., Am. Soc. Test. Mater. 57, 587 (1957).Google Scholar
Lipsitt, H.A. and Wang, D.Y.: The effects of interstitial solute atoms on the fatigue limit behavior of titanium. Trans. Metall. Soc. AIME 221, 918 (1961).Google Scholar
Birnbaum, H.K. and Sofronis, P.: Hydrogen-enhanced localized plasticity—a mechanism for hydrogen-related fracture. Mater. Sci. Eng., A 176, 191 (1994).Google Scholar
Nishikawa, H., Oda, Y., and Noguchi, H.: Investigation of the mechanism for brittle-striation formation in low carbon steel fatigued in hydrogen gas (fractographic observation on fracture processes visualized by controlling load sequence and testing environment). J. Solid Mech. Mater. Eng. 5, 370 (2011).Google Scholar
Doerner, M.F. and Nix, W.D.: A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1, 601 (1986).Google Scholar
Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).Google Scholar
Pharr, G.M., Oliver, W.C., and Brotzen, F.R.: On the generality of the relationship among contact stiffness, contact area, and elastic modulus during indentation. J. Mater. Res. 7, 613 (1992).CrossRefGoogle Scholar
Zorzi, J.E. and Perottoni, C.A.: Estimating Young’s modulus and Poisson’s ratio by instrumented indentation test. Mater. Sci. Eng., A 574, 25 (2013).CrossRefGoogle Scholar
Bucaille, J.L., Stauss, S., Felder, E., and Michler, J.: Determination of plastic properties of metals by instrumented indentation using different sharp indenters. Acta Mater. 51, 1663 (2003).CrossRefGoogle Scholar
Akatsu, T., Demura, T., Shinoda, Y., and Wakai, F.: Evaluation of Young’s modulus and Poisson’s ratio through the analysis of the indentation unloading with finite element method. In Proceedings of the 10th Japan Society of Mechanical Engineers Kanto Branch Conference (Japan Society of Mechanical Engineers: Tokyo, 2004); p. 365.Google Scholar
Bouzakis, K.D. and Michailidis, N.: An accurate and fast approach for determining materials stress–strain curves by nanoindentation and its FEM-based simulation. Mater. Charact. 56, 147–157 (2006).Google Scholar
Kang, J.J., Becker, A.A., and Sun, W.: Determining elastic–plastic properties from indentation data obtained from finite element simulations and experimental results. Int. J. Mech. Sci. 62, 34 (2012).CrossRefGoogle Scholar
Sneddon, I.N.: The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3, 47 (1965).Google Scholar
Field, J.S. and Swain, M.V.: A simple predictive model for spherical indentation. J. Mater. Res. 8, 297 (1993).CrossRefGoogle Scholar
Cheng, Y.T. and Cheng, C.M.: Scaling approach to conical indentation in elastic-plastic solids with work hardening. J. Appl. Phys. 84, 1284 (1998).Google Scholar
Johnson, K.L.: Contact Mechanics (Cambridge University Press, Cambridge, 1987).Google Scholar
Tabor, D.: A simple theory of static and dynamic hardness. Proc. R. Soc. London, Ser. A 192, 247 (1948).Google Scholar
Stilwell, N.A. and Tabor, D.: Elastic recovery of conical indentations. Proc. Phys. Soc. 78, 169 (1961).Google Scholar
Lee, J.H., Lee, H., and Kim, D.H.: A numerical approach to evaluation of elastic modulus using conical indenter with finite tip radius. J. Mater. Res. 23, 2528 (2008).CrossRefGoogle Scholar
Choi, J.H. and Korach, C.S.: Tip bluntness transition measured with atomic force microscopy and the effect on hardness variation with depth in silicon dioxide nanoindentation. Int. J. Precis. Eng. Manuf. 12, 345 (2011).Google Scholar
Mata, M. and Alcalá, J.: The role of friction on sharp indentation. J. Mech. Phys. Solids 52, 145 (2004).Google Scholar
Dugdale, D.S.: Cone indentation experiments. J. Mech. Phys. Solids 2, 265 (1954).Google Scholar
Lee, J.H., Kim, T., and Lee, H.: A study on robust indentation techniques to evaluate elastic–plastic properties of metals. Int. J. Solids Struct. 47, 647 (2010).CrossRefGoogle Scholar
Davies, R.M.: The determination of static and dynamic yield stresses using a steel ball. Proc. R. Soc. London, Ser. A 197, 416 (1949).Google Scholar