Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-18T16:56:59.784Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of the pore shape and dimension on the enhancement of thermoelectric performance of graphene nanoribbons

Published online by Cambridge University Press:  02 February 2017

Sukhdeep Kaur ,
Sukhleen Bindra Narang  and
Deep Kamal Kaur Randhawa
Sukhdeep Kaur
Affiliation:
Department of Electronics Technology, Guru Nanak Dev University, Amritsar 143005, Punjab, India
Sukhleen Bindra Narang*
Affiliation:
Department of Electronics Technology, Guru Nanak Dev University, Amritsar 143005, Punjab, India
Deep Kamal Kaur Randhawa
Affiliation:
Department of Electronics and Communication Engineering, Guru Nanak Dev University, RC Jalandhar, Ladhewali 144007, Punjab, India
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

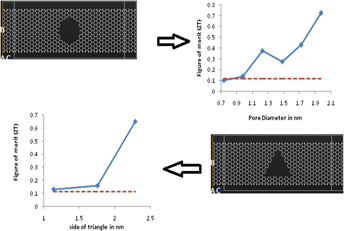
There is a need to discover new thermoelectric materials that can convert waste heat into electrical energy. In this paper, study has been done to observe the effect of shape and dimension of nanopores embedded in graphene nanoribbons (GNRs) as to tune their thermoelectric performance that can lead to enhancement of thermoelectric figure of merit (ZT). It is observed that incorporation of pores in GNRs greatly reduces the thermal conductivity. Although the Seebeck coefficient decreases with the introduction of the pore while the conductance depends upon the pore shape, the decreasing trend in thermal conductivity leads to enhancement of thermoelectric performance. The aim of this work is to study the effect of various circular and the triangular shaped dimensions so as to tune the pore to its optimal dimension that would enhance the overall thermoelectric efficiency. Ballistic transport regime and semiempirical method using Huckel basis set is used to obtain the electrical properties while the Tersoff potential is used for the phononic system.

Keywords

nanostructurethermal conductivity and thermoelectric
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 6 , 28 March 2017 , pp. 1149 - 1159
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Mauricio Terrones

References

REFERENCES

Sadeghi, H., Sangtarash, S., and Lambert, C.J.: Enhanced thermoelectric efficiency of porous silicene nanoribbons. Sci. Rep. 5, 9514 (2015).Google Scholar
Hossain, M.S., Al-Dirini, F., Hossain, F.M., and Skafidas, E.: High performance graphene nano-ribbon thermoelectric devices by incorporation and dimensional tuning of nanopores. Sci. Rep. 5, 11297 (2015).CrossRefGoogle ScholarPubMed
Hicks, L.D. and Dresselhaus, M.S.: Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. B: Condens. Matter Mater. Phys. 47, 16631–16634 (1993).Google Scholar
Karamitaheri, H., Pourfath, M., Faez, R., and Kosina, H.: Geometrical effects on the thermoelectric properties of ballistic graphene antidote lattices. J. Appl. Phys. 110, 05456 (2011).Google Scholar
Nika, D.L. and Balandin, A.A.: Two-dimensional phonon transport in graphene. J. Phys.: Condens. Matter 24, 233203 (2012).Google Scholar
Mingo, N. and Broido, D.A.: Thermoelectric power factor of nanoporous semiconductors. J. Appl. Phys. 101, 014322 (2007).CrossRefGoogle Scholar
Qi, Y., Wang, Z., Zhang, M., Yang, F., and Wang, X.: Thermoelectric devices based on one-dimensional nanostructures. J. Mater. Chem. A 1, 6110 (2013).CrossRefGoogle Scholar
Liu, L. and Chen, X.: Effect of surface roughness on thermal conductivity of silicon nanowires. J. Appl. Phys. 107, 033501 (2010).Google Scholar
Sandhu, J., Seong, M., and Sinha, S.: Partially coherent phonon transport in two-dimensionally rough nanowires. J. Comput. Electron. 11, 1–7 (2012).CrossRefGoogle Scholar
Zhang, G.Q., Yu, Q.X., Wang, W., and Li, X.G.: Nanostructures for thermoelectric applications, synthesis, growth mechanism & property studies. Adv. Mater. 22, 1959–1962 (2012).CrossRefGoogle Scholar
Varshney, V., Roy, A.K., Dudis, D.S., Lee, J., and Farmer, B.L.: A novel nano-configuration for thermoelectric: Helicity induced thermal conductivity reduction in nanowires. Nanoscale 4(16), 5009–5016 (2012).Google Scholar
Zhou, J. and Yang, R.: Ballistic thermoelectricity in double-bend nanowires. Appl. Phys. Lett. 98, 173107 (2011).Google Scholar
Yang, K., Chen, Y., Agosta, R., Xie, Y., Zhong, J., and Rubio, A.: Enhanced thermoelectric properties in hybrid graphene-boron nitride nanoribbons. Phys. Rev. B 86, 045425 (2012).CrossRefGoogle Scholar
Hossain, M.S., Al-Dirini, F., Hossain, F.M., and Skafidas, E.: High performance graphene nano-ribbon thermoelectric devices by incorporation and dimensional tuning of nanopores. Sci. Rep. 5, 11297 (2015).Google Scholar
Chang, P.H. and Nikolic, B.K.: Edge currents and nanopore arrays in zigzag and chiral graphene nanoribbons as a route toward high-ZT thermoelectrics. Phys. Rev. B: Condens. Matter Mater. Phys. 86, 041406(R) (2012).Google Scholar
Chang, P.H., Bahramy, M.S., Nagaosa, N., and Nikolić, B.K.: Giant thermoelectric effect in graphene-based topological insulators with heavy adatoms and nanopores. Nano Lett. 14, 3779–3784 (2014).Google Scholar
Haskins, J., Kinaci, A., Sevik, C., Sevincli, H., Cuniberti, G., and Cagin, T.: Control of thermal and electronic transport in defect-engineered graphene nanoribbons. ACS Nano 5, 3779–3787 (2011).Google Scholar
Yijian, O. and Jing, G.: A theoretical study on thermoelectric properties of graphene nanoribbons. Appl. Phys. Lett. 94, 263107 (2009).Google Scholar
Saiz-Bretin, M., Malyshev, A.V., Orellana, P.A., and Adame, F.D.: Enhancing thermoelectric properties of graphene quantum rings. Phys. Rev. B 91, 085431 (2015).Google Scholar
Mazzamuto, F., Nguyen, V.H., Apertet, Y., Chassat, C., Saint-Martin, J., and Dollfus, P.: Enhanced thermoelectric properties in graphene nanoribbons by resonant tunneling of electrons. Phys. Rev. B: Condens. Matter Mater. Phys. 83, 235426 (2011).Google Scholar
Liang, L.B., Cruz-Silva, E., Girao, E.C., and Meunier, V.: Enhanced thermoelectric figure of merit in assembled graphene nanoribbons. Phys. Rev. B: Condens. Matter Mater. Phys. 86, 115438 (2012).Google Scholar
Sevincli, H. and Cuniberti, G.: Enhanced thermoelectric figure of merit in edge-disordered zigzag graphene nanoribbons. Phys. Rev. B: Condens. Matter Mater. Phys. 81, 113401–113404 (2010).Google Scholar
Checkelsky, J.G. and Ong, N.P.: Thermopower and Nernst effect in graphene in a magnetic field. Phys. Rev. B: Condens. Matter Mater. Phys. 80, 081413 (2009).Google Scholar
Wang, D. and Shi, J.: Effect of charged impurities on the thermoelectric power of graphene near the Dirac point. Phys. Rev. B: Condens. Matter Mater. Phys. 83, 113403 (2011).CrossRefGoogle Scholar
Wei, P., Bao, W., Pu, Y., Lau, C.N., and Shi, J.: Anomalous thermoelectric transport of Dirac particles in graphene. Phys. Rev. Lett. 102, 166808 (2009).Google Scholar
Mazzamuto, F., Nguyen, V.H., Apertet, Y., Caer, C., Chassat, C., Saint-Martin, J., and Dollfus, P.: Enhanced thermoelectric properties in graphene nanoribbons by resonant tunneling of electrons. Phys. Rev. B: Condens. Matter Mater. Phys. 83, 235426 (2011).Google Scholar
Liang, L.B., Cruz-Silva, E., Girao, E.C., and Meunier, V.: Enhanced thermoelectric figure of merit in assembled graphene nanoribbons. Phys. Rev. B: Condens. Matter Mater. Phys. 86, 115438 (2012).Google Scholar
Mazzamuto, F., Saint-Martin, J., Nguyen, V.H., Chassat, C., and Dollfus, P.: Thermoelectric performance of disordered and nanostructured graphene ribbons using Green’s function method. J. Comput. Electron. 11, 67–77 (2012).Google Scholar
Han, M.Y., Ozyilmaz, B., Zhang, Y.B., and Kim, P.: Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 98, 206805 (2007).Google Scholar
Bai, J., Duan, X., and Huang, Y.: Rational fabrication of graphene nanoribbons using a nanowire etch mask. Nano Lett. 9, 2083–2087 (2009).CrossRefGoogle ScholarPubMed
Wei, Z., Qiang, Z., Meng-Qiang, Z., and Kuhn, L.T.: Direct writing on graphene ‘paper’ by manipulating electrons as ‘invisible ink’. Nanotechnology 24, 1–6 (2013).Google Scholar
Tapaszto, L., Dobrik, G., Lambin, P., and Biro, L.P.: Tailoring the atomic structure of graphene nanoribbons by scanning tunneling microscope lithography. Nat. Nanotechnol. 3, 397–401 (2008).Google Scholar
Kalhor, N., Boden, S.A., and Mizuta, H.: Sub-10 nm patterning by focused He-ion beam milling for fabrication of downscaled graphene nano devices. Microelectron. Eng. 114, 70–77 (2014).Google Scholar
Abbas, A.N., Liu, G., Liu, B., Zhang, L., Liu, H., Ohlberg, D., Wu, W., and Zhou, C.: Patterning, characterization, and chemical sensing applications of graphene nanoribbon arrays down to 5 nm using helium ion beam lithography. ACS Nano 8, 1538–1546 (2014).Google Scholar
Esfarjani, K., Zebarjadi, M., and Kawazoe, Y.: Thermoelectric properties of a nanocontact made of two-capped single-wall carbon nanotubes calculated within the tight-binding approximation. Phys. Rev. B: Condens. Matter Mater. Phys. 73, 085406 (2006).CrossRefGoogle Scholar
Sadeghi, H., Sangtarash, S., and Lambert, C.J.: Enhancing the thermoelectric figure of merit in engineered graphene nanoribbons. Beilstein J. Nanotechnol. 6, 1176–1182 (2015).Google Scholar
Kienle, D., Cerda, J.I., and Ghosh, A.W.: Extended Huckel theory for band structure, chemistry, and transport. Carbon nanotubes. J. Appl. Phys. 100, 043714 (2006).Google Scholar
Landauer, R.: Spatial variation of currents and fields due to localized scatterers in metallic conduction. IBM. J. Res. Dev. 1, 223–231 (1957).CrossRefGoogle Scholar
Stokbro, K., Peterson, D.E., Smidstrup, S., Blom, A., Ipsen, M., and Kaasbjerg, K.: Semiempirical model for nanoscale device simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 82, 075420 (2010).Google Scholar
Chen, J.H., Jang, C., Xiao, S., Ishigami, M., and Fuhrer, M.S.: Intrinsic and extrinsic performance limits of graphene devices on SiO2 . Nat. Nano. 3, 206–209 (2008).Google Scholar
PengTao, X.U., Xiang, Y.J., Sai, W.K., Zhen, Z., and PanWen, S.: Porous graphene: Properties, preparation, and potential applications. Chinese Sci. Bull. 57, 2948–2955 (2012).Google Scholar
Zheng, X.H., Huang, L.F., Wang, X.L., Lan, J., and Zeng, Z.: Band gap engineering in armchair-edged graphene nanoribbons by edge dehydrogenation. Comput. Mater. Sci. 62, 93–98 (2012).CrossRefGoogle Scholar
Vanin, M., Gath, J., Thygesen, K.S., and Jacobsen, K.W.: First-principles calculations of graphene nanoribbons in gaseous environments. Phys. Rev. B: Condens. Matter Mater. Phys. 82, 195411 (2010).Google Scholar
Pan, L., Liu, H.J., Tan, X.J., Lv, H.Y., Shi, J., Tang, X.F., and Zheng, G.: Thermoelectric properties of armchair and zigzag silicene nanoribbons. Phys. Chem. Chem. Phys. 14, 13588–13593 (2012).CrossRefGoogle ScholarPubMed
Kaur, M., Sawhney, R.S., and Engles, D.: Non-equilibrium tunneling through Au–C20–Au molecular bridge using density functional theory-non-equilibrium Green function approach. J. Mater. Res. 31(14), 2025–2034 (2016).Google Scholar