Article contents
Effect of segregated Al on 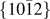 $\left\{ {10\bar 12} \right\}$ and
$\left\{ {10\bar 12} \right\}$ and 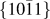 $\left\{ {10\bar 11} \right\}$ twinning in Mg
$\left\{ {10\bar 11} \right\}$ twinning in Mg
Published online by Cambridge University Press: 03 November 2015
Abstract
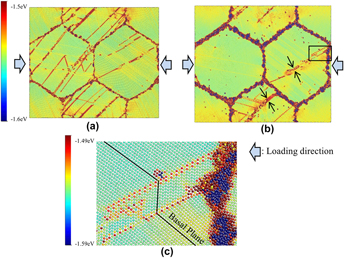
Molecular dynamics simulations of compression deformation of  $\left[ {11\bar 20} \right]$-textured 2-dimensional polycrystalline pure Mg, Mg–0.1 at.%Al, and Mg–1.0 at.%Al models were performed at 5 and 300 K. A
$\left[ {11\bar 20} \right]$-textured 2-dimensional polycrystalline pure Mg, Mg–0.1 at.%Al, and Mg–1.0 at.%Al models were performed at 5 and 300 K. A  $\left\{ {10\bar 11} \right\}$ twin nucleated before formation of a
$\left\{ {10\bar 11} \right\}$ twin nucleated before formation of a  $\left\{ {10\bar 12} \right\}$ twin in the simulations at 5 K, while a
$\left\{ {10\bar 12} \right\}$ twin in the simulations at 5 K, while a  $\left\{ {10\bar 11} \right\}$ twin nucleated after formation of a
$\left\{ {10\bar 11} \right\}$ twin nucleated after formation of a  $\left\{ {10\bar 12} \right\}$ twin in the simulations at 300 K. The formation of a
$\left\{ {10\bar 12} \right\}$ twin in the simulations at 300 K. The formation of a  $\left\{ {10\bar 11} \right\}$ twin was the result of the glide of pyramidal 〈c + a〉 partial dislocations of
$\left\{ {10\bar 11} \right\}$ twin was the result of the glide of pyramidal 〈c + a〉 partial dislocations of  ${1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6}\left\{ {10\bar 11} \right\}\left[ {\bar 2023} \right]$.
${1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6}\left\{ {10\bar 11} \right\}\left[ {\bar 2023} \right]$.  $\left\{ {10\bar 11} \right\}$ twin formation was suppressed at the sites around the Al atoms because the strong Mg–Al bond suppresses atomic shuffling. However, formation was not suppressed at the sites away from the Al atoms because the effect of strong Mg–Al bond is short range. On the other hand, because
$\left\{ {10\bar 11} \right\}$ twin formation was suppressed at the sites around the Al atoms because the strong Mg–Al bond suppresses atomic shuffling. However, formation was not suppressed at the sites away from the Al atoms because the effect of strong Mg–Al bond is short range. On the other hand, because  $\left\{ {10\bar 12} \right\}$ twinning requires the simultaneous glide of zonal dislocations, Al inevitably suppressed
$\left\{ {10\bar 12} \right\}$ twinning requires the simultaneous glide of zonal dislocations, Al inevitably suppressed  $\left\{ {10\bar 12} \right\}$ twinning.
$\left\{ {10\bar 12} \right\}$ twinning.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2015
References
REFERENCES
- 13
- Cited by


