Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T06:33:42.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-continuum study of the buckling behavior of single-walled carbon nanocones subjected to bending under thermal loading

Published online by Cambridge University Press:  22 May 2017

Xiangyang Wang ,
Huibo Qi ,
Zhongyu Sun ,
Xiaojing Wang ,
Xiushu Song ,
Jinbao Wang  and
Xu Guo
Xiangyang Wang*
Affiliation:
School of Transportation, Ludong University, Yantai 264025, Shandong, China
Huibo Qi
Affiliation:
School of Transportation, Ludong University, Yantai 264025, Shandong, China
Zhongyu Sun
Affiliation:
School of Transportation, Ludong University, Yantai 264025, Shandong, China
Xiaojing Wang
Affiliation:
School of Transportation, Ludong University, Yantai 264025, Shandong, China
Xiushu Song
Affiliation:
School of Transportation, Ludong University, Yantai 264025, Shandong, China
Jinbao Wang
Affiliation:
School of Shipping and Ports Architecture Engineering, Zhejiang Ocean University, Zhoushan 316022, China
Xu Guo*
Affiliation:
State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian 116023, China
*
a) Address all correspondence to these authors. e-mail: [email protected]
b) e-mail: [email protected]
Get access

Abstract

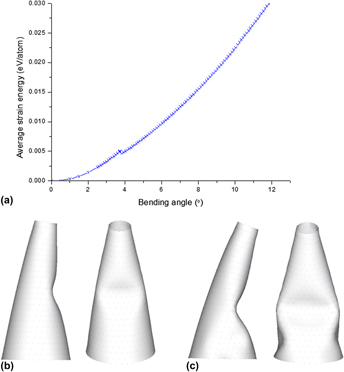
In this study, the buckling behaviors of single-walled carbon nanocones (SWCNCs) under bending at finite temperatures are predicted using a proposed multiscale quasi-continuum approach based on the temperature-dependent higher order Cauchy–Born (THCB) rule. The hyper-elastic constitutive model is derived exactly in the context of the higher order gradient theory that incorporates the details of the interatomic interaction. The numerical simulations for the deformation of SWCNCs are implemented using the developed meshless computational framework based on moving least-squares interpolation, which can precisely reproduce the deformation process and buckling patterns of SWCNCs under bending. The underlying correlations of the critical bending angle with respect to the geometry of SWCNCs and temperature are revealed by the numerical results. Furthermore, our simulation captures the transformation from the local to the global buckling process of SWCNCs, accompanied with an average strain energy jump. Our results correspond with previous studies.

Keywords

nanoscalenanostructuresimulationbuckling
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 12 , 28 June 2017 , pp. 2266 - 2275
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Susan B. Sinnott

References

REFERENCES

Ge, M.H. and Sattler, K.: Observation of fullerene cones. Chem. Phys. Lett. 220, 192 (1994).Google Scholar
Charlier, J.C. and Rignanese, G.M.: Electronic structure of carbon nanocones. Phys. Rev. Lett. 86, 5970 (2001).CrossRefGoogle ScholarPubMed
Yan, J.W., Liew, K.M., and He, L.H.: Ultra-sensitive analysis of a cantilevered single walled carbon nanocone-based mass detector. Nanotechnology 24, 176 (2013).Google Scholar
Majidi, R. and Tabrizi, K.G.: Study of neon adsorption on carbon nanocones using molecular dynamics simulation. Phys. B 405, 2144 (2010).CrossRefGoogle Scholar
Narjabadifam, A., Vakili-Tahami, F., Zehsaz, M., and Fakhrabadi, M.M.S.: Three-dimensional modal analysis of carbon nanocones using molecular dynamics simulation. J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom. 33, 051805 (2015).Google Scholar
Fakhrabadi, M.M.S., Khani, N., Omidvar, R., and Rastgoo, A.: Investigation of elastic and buckling properties of carbon nanocones using molecular mechanics approach. Comput. Mater. Sci. 61, 248 (2012).CrossRefGoogle Scholar
Liew, K.M., Wei, J.X., and He, X.Q.: Carbon nanocones under compression: Buckling and post-buckling behaviors. Phys. Rev. B 75, 195435 (2007).CrossRefGoogle Scholar
Jordan, S.P. and Crespi, V.H.: Theory of carbon nanocones: Mechanical chiral inversion of a micron-scale three-dimensional object. Phys. Rev. Lett. 93, 255504 (2004).CrossRefGoogle ScholarPubMed
Ansari, R. and Mahmoudinezhad, E.: Characterizing the mechanical properties of carbon nanocones using an accurate spring-mass model. Comput. Mater. Sci. 101, 260 (2015).CrossRefGoogle Scholar
Ansari, R., Sadeghi, F., and Darvizeh, M.: Continuum study on the oscillatory characteristics of carbon nanocones inside single-walled carbon nanotubes. Phys. B 482, 28 (2016).CrossRefGoogle Scholar
Lee, J.H. and Lee, B.S.: Modal analysis of carbon nanotubes and nanocones using FEM. Comput. Mater. Sci. 51, 30 (2012).Google Scholar
Yan, J.W., Liew, K.M., and He, L.H.: Predicting mechanical properties of single-walled carbon nanocones using a higher-order gradient continuum computational framework. Compos. Struct. 94, 3271 (2012).CrossRefGoogle Scholar
Yan, J.W., Liew, K.M., and He, L.H.: A mesh-free computational framework for predicting buckling behaviors of single-walled carbon nanocones under axial compression based on the moving Kriging interpolation. Comput. Meth. Appl. Mech. Eng. 247–248, 103 (2012).Google Scholar
Yan, J.W., Liew, K.M., and He, L.H.: Buckling and post-buckling of single-wall carbon nanocones upon bending. Compos. Struct. 106, 793 (2013).Google Scholar
Tsai, P.C. and Fang, T.H.: A molecular dynamics study of the nucleation, thermal stability and nanomechanics of carbon nanocones. Nanotechnology 18, 105702 (2007).Google Scholar
Liao, M.L., Cheng, C.H., and Lin, Y.P.: Tensile and compressive behaviors of open-tip carbon nanocones under axial strains. J. Mater. Res. 26, 1577 (2011).CrossRefGoogle Scholar
Liao, M.L.: Buckling behaviors of open-tip carbon nanocones at elevated temperatures. Appl. Phys. A 117, 1109 (2014).CrossRefGoogle Scholar
Wang, X.Y., Wang, J.B., and Guo, X.: Finite deformation of single-walled carbon nanocones under axial compression using a temperature-related multiscale quasi-continuum model. Comput. Mater. Sci. 114, 244 (2016).Google Scholar
Compernolle, S., Kiran, B., Chibotaru, L.F., Nguyen, M.T., and Ceulemans, A.: Ab initio study of small graphitic cones with triangle, square, and pentagon apex. J. Chem. Phys. 121, 2326 (2004).Google Scholar
Guo, X., Liao, J.B., and Wang, X.Y.: Investigation of the thermo-mechanical properties of single-walled carbon nanotubes based on the temperature-related higher order Cauchy–Born rule. Comput. Mater. Sci. 51, 445 (2012).CrossRefGoogle Scholar
Wang, X.Y. and Guo, X.: Numerical simulation for finite deformation of single-walled carbon nanotubes at finite temperature using temperature-related higher order Cauchy–Born rule based quasi-continuum model. Comput. Mater. Sci. 55, 273 (2012).Google Scholar
Wang, X.Y. and Guo, X.: Quasi-continuum contact model for the simulation of severe deformation of single-walled carbon nanotubes at finite temperature. J. Comput. Theor. Nanosci. 10, 810 (2013).CrossRefGoogle Scholar
Wang, X.Y. and Guo, X.: Quasi-continuum model for the finite deformation of single-layer graphene sheets based on the temperature-related higher order Cauchy–Born rule. J. Comput. Theor. Nanosci. 10, 154 (2013).Google Scholar
Arroyo, M. and Belytschko, T.: An atomistic-based finite deformation membrane for single layer crystalline films. J. Mech. Phys. Solids 50, 1941 (2002).CrossRefGoogle Scholar
Arroyo, M. and Belytschko, T.: Finite element methods for the non-linear mechanics of crystalline sheets and nanotubes. Int. J. Numer. Methods Eng. 59, 419 (2004).Google Scholar
Sun, Y.Z. and Liew, K.M.: Application of the higher-order Cauchy–Born rule in mesh-free continuum and multi-scale simulation of carbon nanotubes. Int. J. Numer. Methods Eng. 75, 1238 (2008).Google Scholar
Foiles, S.M.: Evaluation of harmonic methods for calculating the free energy of defects in solids. Phys. Rev. B 49, 14930 (1994).Google Scholar
Najafabadi, R. and Srolovitz, D.J.: Evaluation of the accuracy of the free-energy-minimization method. Phys. Rev. B 52, 9229 (1995).CrossRefGoogle ScholarPubMed
Jiang, H., Huang, Y., and Hwang, K.C.: A finite-temperature continuum theory based on interatomic potentials. J. Eng. Mat. Phys. Rev. B 52, 9229 (1995).Google Scholar
Tersoff, J.: New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 37, 6991 (1988).CrossRefGoogle ScholarPubMed
Brenner, D.W.: Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 42, 9458 (1990).Google Scholar
Lancaster, P. and Salkauskas, K.: Surfaces generated by moving least squares methods. Math. Comput. 37, 141 (1981).CrossRefGoogle Scholar
Dolbow, J. and Belytschko, T.: An introduction to programming the meshless element free Galerkin method. Arch. Comput. Meth. Eng. 5, 207 (1998).Google Scholar
Meyer, J.C., Geim, A.K., Katsnelson, M.I., Novoselov, K.S., Booth, T.J., and Roth, S.: The structure of suspended graphene sheets. Nature 446, 60 (2007).Google Scholar
Fasolino, A., Los, J.H., and Katsnelson, M.I.: Intrinsic ripples in graphene. Nat. Mater. 6, 858 (2007).CrossRefGoogle ScholarPubMed
Shen, L., Shen, H.S., and Zhang, C.L.: Temperature-dependent elastic properties of single layer graphene sheets. Mater. Des. 31, 4445 (2010).Google Scholar