Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T05:24:44.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Atomistic investigation of crack growth resistance in a single-crystal Al-nanoplate

Published online by Cambridge University Press:  19 April 2016

Xiao Ru Zhuo ,
Jang Hyun Kim  and
Hyeon Gyu Beom
Xiao Ru Zhuo
Affiliation:
Department of Mechanical Engineering, Inha University, Incheon 402-751, Republic of Korea
Jang Hyun Kim
Affiliation:
Department of Mechanical Engineering, Inha University, Incheon 402-751, Republic of Korea
Hyeon Gyu Beom*
Affiliation:
Department of Mechanical Engineering, Inha University, Incheon 402-751, Republic of Korea
*
a) Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

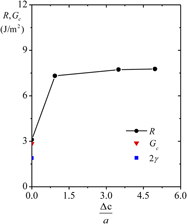
The fracture behavior of a single-crystal Al-nanoplate with an edge crack under tensile loading was simulated using a molecular statics technique to evaluate crack growth resistance in Al. The crack length was determined using a stiffness method. A parabolic function fitted from simulation results was used to predict the crack length from the stiffness value extracted from unloading curves. Based on energy considerations, crack growth resistance was calculated. Crack growth resistance rose sharply in the initial stages of crack growth, and with an additional crack extension, it increased gradually to converge to a constant far exceeding the fracture toughness predicted by the Griffith criterion. This trend in the crack growth resistance curve was closely related to the amorphous zone formed at the crack tip after the onset of crack propagation.

Keywords

fracturenanostructuresimulation
Type
Articles
Information
Journal of Materials Research , Volume 31 , Issue 9 , 14 May 2016 , pp. 1185 - 1192
Copyright
Copyright © Materials Research Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Stranz, A., Waag, A., and Peiner, E.: Thermal characterization of vertical silicon nanowires. J. Mater. Res. 26, 1958 (2011).CrossRefGoogle Scholar
Lu, L., Shen, Y., Chen, X., Qian, L., and Lu, K.: Ultrahigh strength and high electrical conductivity in copper. Science 304, 422 (2004).CrossRefGoogle ScholarPubMed
Alexandrov, A.S. and Kabanov, V.V.: Magnetic quantum oscillations in nanowires. Phys. Rev. Lett. 95, 76601 (2005).CrossRefGoogle ScholarPubMed
Zhuo, X.R. and Beom, H.G.: Molecular statics simulations of the size-dependent mechanical properties of copper nanofilms under shear loading. Comput. Mater. Sci. 99, 390 (2015).CrossRefGoogle Scholar
Maxwell, D.J., Emory, S.R., and Nie, S.: Nanostructured thin-film materials with surface-enhanced optical properties. Chem. Mater. 13, 1082 (2001).CrossRefGoogle Scholar
Cui, Y., Wei, Q., Park, H., and Lieber, C.M.: Nanowire nanosensors for highly sensitive and selective detection of biological and chemical species. Science 293, 1289 (2001).CrossRefGoogle ScholarPubMed
Jensen, K., Girit, C., Mickelson, W., and Zettl, A.: Tunable nanoresonators constructed from telescoping nanotubes. Phys. Rev. Lett. 96, 215503 (2006).CrossRefGoogle ScholarPubMed
Sul, O. and Yang, E.: A multi-walled carbon nanotube–aluminum bimorph nanoactuator. Nanotechnology 20, 95502 (2009).CrossRefGoogle ScholarPubMed
Legoas, S.B., Coluci, V.R., Braga, S.F., Coura, P.Z., Dantas, S.O., and Galvao, D.S.: Molecular-dynamics simulations of carbon nanotubes as gigahertz oscillators. Phys. Rev. Lett. 90, 55504 (2003).CrossRefGoogle ScholarPubMed
Wang, Z.L. and Song, J.: Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 312, 242 (2006).CrossRefGoogle ScholarPubMed
Buehler, M.J., Abraham, F.F., and Gao, H.: Hyperelasticity governs dynamic fracture at a critical length scale. Nature 426, 141 (2003).CrossRefGoogle Scholar
Diao, J., Gall, K., and Dunn, M.L.: Surface-stress-induced phase transformation in metal nanowires. Nat. Mater. 2, 656 (2003).CrossRefGoogle ScholarPubMed
Cui, C.B. and Beom, H.G.: Molecular dynamics simulations of edge cracks in copper and aluminum single crystals. Mater. Sci. Eng., A 609, 102 (2014).CrossRefGoogle Scholar
Zhuo, X.R. and Beom, H.G.: Size-dependent fracture properties of cracked silicon nanofilms. Mater. Sci. Eng., A 636, 470 (2015).CrossRefGoogle Scholar
Farkas, D.: Fracture resistance of nanocrystalline Ni. Metall. Mater. Trans. A 38, 2168 (2007).CrossRefGoogle Scholar
Farkas, D., Van Swygenhoven, H., and Derlet, P.M.: Intergranular fracture in nanocrystalline metals. Phys. Rev. B: Condens. Matter Mater. Phys. 66, 60101 (2002).CrossRefGoogle Scholar
Kalia, R.K., Nakano, A., Omeltchenko, A., Tsuruta, K., and Vashishta, P.: Role of ultrafine microstructures in dynamic fracture in nanophase silicon nitride. Phys. Rev. Lett. 78, 2144 (1997).CrossRefGoogle Scholar
Baker, K.L. and Warner, D.H.: Extended timescale atomistic modeling of crack tip behavior in aluminum. Modell. Simul. Mater. Sci. Eng. 20, 65005 (2012).CrossRefGoogle Scholar
Krull, H. and Yuan, H.: Suggestions to the cohesive traction–separation law from atomistic simulations. Eng. Fract. Mech. 78, 525 (2011).CrossRefGoogle Scholar
Ippolito, M., Mattoni, A., Pugno, N., and Colombo, L.: Failure strength of brittle materials containing nanovoids. Phys. Rev. B: Condens. Matter Mater. Phys. 75, 224110 (2007).CrossRefGoogle Scholar
Mishin, Y., Farkas, D., Mehl, M.J., and Papaconstantopoulos, D.A.: Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 59, 3393 (1999).CrossRefGoogle Scholar
Tsai, D.H.: The virial theorem and stress calculation in molecular dynamics. J. Chem. Phys. 70, 1375 (1979).CrossRefGoogle Scholar
Subramaniyan, A.K. and Sun, C.T.: Continuum interpretation of virial stress in molecular simulations. Int. J. Solids Struct. 45, 4340 (2008).CrossRefGoogle Scholar
Plimpton, S.: Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1 (1995).CrossRefGoogle Scholar
Li, J.: AtomEye: An efficient atomistic configuration viewer. Modell. Simul. Mater. Sci. Eng. 11, 173 (2003).CrossRefGoogle Scholar
Farkas, D., Duranduru, M., Curtin, W.A., and Ribbens, C.: Multiple-dislocation emission from the crack tip in the ductile fracture of Al. Philos. Mag. A 81, 1241 (2001).CrossRefGoogle Scholar
Hoagland, R.G., Daw, M.S., Foiles, S.M., and Baskes, M.I.: An atomic model of crack tip deformation in aluminum using an embedded atom potential. J. Mater. Res. 5, 313 (1990).CrossRefGoogle Scholar
Kimizuka, H., Kaburaki, H., Shimizu, F., and Li, J.: Crack-tip dislocation nanostructures in dynamical fracture of fcc metals: A molecular dynamics study. J. Comput.-Aided Mol. Des. 10, 143 (2003).Google Scholar
Stukowski, A. and Albe, K.: Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Modell. Simul. Mater. Sci. Eng. 18, 85001 (2010).CrossRefGoogle Scholar
Anderson, T.L.: Fracture Mechanics: Fundamentals and Applications, 3rd ed. (CRC Press, Boca Raton, 2005).CrossRefGoogle Scholar
Eftis, J. and Liebowitz, H.: On fracture toughness evaluation for semi-brittle fracture. Eng. Fract. Mech. 7, 101 (1975).CrossRefGoogle Scholar
Griffith, A.A.: The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. A. 221, 163 (1921).Google Scholar
Hung, L. and Carter, E.A.: Ductile processes at aluminium crack tips: Comparison of orbital-free density functional theory with classical potential predictions. Modell. Simul. Mater. Sci. Eng. 19, 45002 (2011).CrossRefGoogle Scholar
White, P.: Molecular dynamic modelling of fatigue crack growth in aluminium using LEFM boundary conditions. Int. J. Fatigue. 44, 141 (2012).CrossRefGoogle Scholar
Hoagland, R.G., Daw, M.S., and Hirth, J.P.: Some aspects of forces and fields in atomic models of crack tips. J. Mater. Res. 6, 2565 (1991).CrossRefGoogle Scholar
Nair, A.K., Warner, D.H., and Hennig, R.G.: Coupled quantum–continuum analysis of crack tip processes in aluminum. J. Mech. Phys. Solids 59, 2476 (2011).CrossRefGoogle Scholar
Beltz, G.E., Lipkin, D.M., and Fischer, L.L.: Role of crack blunting in ductile versus brittle response of crystalline materials. Phys. Rev. Lett. 82, 4468 (1999).CrossRefGoogle Scholar
Gómez, F.J. and Elices, M.: Fracture loads for ceramic samples with rounded notches. Eng. Fract. Mech. 73, 880 (2006).CrossRefGoogle Scholar
Hoagland, R.G.: Crystallographic aspects of dislocation emission from a crack tip in an fcc metal. Philos. Mag. A 76, 543 (1997).CrossRefGoogle Scholar
Gerberich, W.W., Huang, H., Zielinski, W., and Marsh, P.G.: A dislocation shielding prediction of the toughness transition during cleavage of semibrittle crystals. Metall. Mater. Trans. A 24, 535 (1993).CrossRefGoogle Scholar
Tvergaard, V. and Hutchinson, J.W.: Effect of strain-dependent cohesive zone model on predictions of crack growth resistance. Int. J. Solids Struct. 33, 3297 (1996).CrossRefGoogle Scholar