Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T18:29:33.244Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants birationnels dans la suite spectrale de Bloch-Ogus

Published online by Cambridge University Press:  07 June 2012

Alena Pirutka
Alena Pirutka*
Affiliation:
IRMA - Université de Strasbourg, 7 rue René Descartes, 67084 Strasbourg Cedex, [email protected]
Get access

Abstract

For a field k of cohomological dimension d we prove that the groups 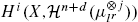, (l, car.k) = 1, are birational invariants of smooth projective geometrically integral varieties over k of dimension n. Using the Kato conjecture, which has been recently established by Kerz and Saito [18], we obtain a similar result over a finite field for the groups 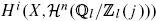. We relate one of these invariants with the cokernel of the l-adic cycle class map 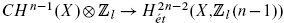, which gives an analogue of a result of Colliot-Thélène and Voisin [5] 3.11 over ℂ for varieties over a finite field.

Résumé

On établit l'invariance birationnelle des groupes 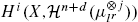pour X une variété projective et lisse, géométriquement intègre, de dimension n, définie sur un corps k de dimension cohomologique au plus d, (l, car.k) = 1. En utilisant la conjecture de Kato, démontrée récémment par Kerz et Saito [18], on obtient aussi un résultat analogue sur un corps fini pour les groupes 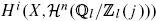et on relie un de ces invariants avec le conoyau del'application classe de cycle 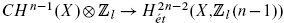, ce qui donne une version sur un corps fini d'fun résultat de Colliot-Thélène et Voisin [5] 3.11 sur le corps des complexes.

Keywords

invariants birationnelsmodules de cyclessuite spectrale de Bloch-Ogusapplication classe de cycle (birational invariants, cycle modules, Bloch-Ogus spectral sequence, cycle class map)
Type
Research Article
Information
Journal of K-Theory , Volume 10 , Issue 3 , December 2012 , pp. 565 - 582
Copyright
Copyright © ISOPP 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

1.Bloch, S., Ogus, A., Gersten's conjecture and the homology of schemes, Ann. Sci. École Norm. Sup. (4) 7 (1974), 181–201 (1975).Google Scholar
2.Colliot-Thélène, J.-L., Birational invariants, purity and the Gersten conjecture, K-theory and algebraic geometry : connections with quadratic forms and division algebras (Santa Barbara, CA, 1992), 1–64, Proc. Sympos. Pure Math. 58, Part 1, Amer. Math. Soc., Providence, RI, 1995.Google Scholar
3.Colliot-Thélène, J.-L., Conjectures de type local-global sur l'image des groupes de Chow dans la cohomologie étale, Algebraic K-theory (Seattle,WA, 1997), 1–12, Proc. Sympos. Pure Math. 67, Amer. Math. Soc., Providence, RI, 1999.Google Scholar
4.Colliot-Thélène, J.-L. et Kahn, B., Cycles de codimension 2 et H3 non ramifié pour les variétés sur les corps finis, arXiv :1104.3350v1.Google Scholar
5.Colliot-Thélène, J.-L. et Voisin, C., Cohomologie non ramifiée et conjecture de Hodge entière, arXiv :1005.2778v1, à paraître dans Duke Mathematical Journal.Google Scholar
6.Déglise, F., Transferts sur les groupes de Chow à coefficients, Math. Z. 252 (2006), no. 2. 315–343.Google Scholar
7.Fulton, W., Intersection theory, Springer-Verlag, Berlin, 1998.Google Scholar
8.Grothendieck, A., Sur quelques points d'algèbre homologique, Tôhoku Math. J. (2) 9 (1957), 119–221.Google Scholar
9.Illusie, L., On Gabber's refined uniformization, disponible sur http://www.math.upsud.fr/~illusie/Google Scholar
10.Jannsen, U. and Saito, S., Kato conjecture and motivic cohomology over finite fields, arXiv :0910.2815.Google Scholar
11.Kahn, B., Résultats de “pureté” pour les variétés lisses sur un corps fini (appendice à un article de J.-L. Colliot-Thélène), Actes du Colloque de K-théorie algébrique de Lake Louise, décembre 1991 (P.G Goerss, J.F. Jardine, ed.), Algebraic K-theory and algebraic topology, NATO ASI Series, Ser. C. 407 (1993), 57–62.Google Scholar
12.Kahn, B., Deux théorèmes de comparaison en cohomologie étale : applications, Duke Math. J. 69 (1993), no. 1, 137–165.Google Scholar
13.Kahn, B., Motivic cohomology of smooth geometrically cellular varieties, Algebraic K-theory (Seattle,WA, 1997), 149–174, Proc. Sympos. Pure Math. 67, Amer. Math. Soc., Providence, RI, 1999.Google Scholar
14.Kahn, B., Équivalences rationnelle et numérique sur certaines variétés de type abélien sur un corps fini, Ann. Sci. École Norm. Sup. (4) 36 (2003), no. 6, 977–1002 (2004).Google Scholar
15.Kahn, B., Cohomological approaches to SK1 and SK2 of central simple algebras, Documenta Mathematica, Extra Volume : Andrei A. Suslin's Sixtieth Birthday (2010), 317–369.Google Scholar
16.Kahn, B., Classes de cycles motiviques étales, arXiv :1102.0375v2, à paraître dans Algebra and Number Theory.Google Scholar
17.Kato, K., A Hasse principle for two-dimensional global fields, J. reine angew. Math. 366 (1986), 142–183.Google Scholar
18.Kerz, M. and Saito, S., Cohomological Hasse principle and motivic cohomology for arithmetic schemes, arXiv :1010.5930v1, to appear in Publ. Math. IHES.Google Scholar
19.Manin, Yu. I., Le groupe de Brauer-Grothendieck en géométrie diophantienne, Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, pp. 401–411. Gauthier-Villars, Paris, 1971.Google Scholar
20.Milne, J.S., Values of zeta functions of varieties over finite fields, Amer. J. Math. 108 (1986), no. 2, 297–360.Google Scholar
21.Rost, M., Chow groups with coefficients, Doc. Math. 1 (1996), No. 16, 319–393.Google Scholar
22.Saito, S., Some observations on motivic cohomology of arithmetic schemes, Invent. Math. 98 (1989), no. 2, 371–404.Google Scholar
23.Saito, S. and Sato, K., A finiteness theorem for zero-cycles over p-adic fields, with an appendix by U. Jannsen, Ann. of Math. (2) 172 (2010), no. 3, 1593–1639.Google Scholar
24.Serre, J-P., Cohomologie galoisienne, Lecture Notes in Mathematics 5, Springer-Verlag, Berlin, 1994.Google Scholar
25.Voevodsky, V., On motivic cohomology with ℤ/l coefficients, arXiv :0805.4430v2, à paraître dans Ann. of Math.Google Scholar