Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T06:31:37.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactly supported analytic indices for Lie groupoids

Published online by Cambridge University Press:  12 October 2009

Paulo Carrillo Rouse
Paulo Carrillo Rouse
Affiliation:
Projet d'algèbres d'opérateurs, Université de Paris 7, 175, rue de Chevaleret, Paris, France, [email protected]
Get access

Abstract

For any Lie groupoid we construct an analytic index morphism taking values in a modified K-theory group which involves the convolution algebra of compactly supported smooth functions over the groupoid. The construction is performed by using the deformation algebra of smooth functions over the tangent groupoid constructed in [CR06]. This allows us in particular to prove a more primitive version of the Connes-Skandalis longitudinal index theorem for foliations, that is, an index theorem taking values in a group which pairs with cyclic cocycles. As another application, for D a 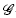-PDO elliptic operator with associated index ind 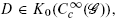we prove that the pairing

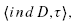
with τ a bounded continuous cyclic cocycle, only depends on the principal symbol class [σ(D)]∈K0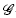. The result is completely general for étale groupoids. We discuss some potential applications to the Novikov conjecture.

Keywords

Lie groupoidsTangent groupoidK-theoryCyclic cohomologyIndex theory
Type
Research Article
Information
Journal of K-Theory , Volume 4 , Issue 2 , October 2009 , pp. 223 - 262
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

ANS06.Aastrup, Johannes, Nest, Ryszard, and Schrohe, Elmar. A continuous field of C*- algebras and the tangent groupoid for manifolds with boundary. J. Funct. Anal., 237(2):482–506, 2006.CrossRefGoogle Scholar
AS68.Atiyah, M. F. and Singer, I. M.. The index of elliptic operators. I.. Ann. of Math. (2), 87:484–530, 1968.Google Scholar
BC00.Baum, Paul and Connes, Alain. Geometric K-theory for Lie groups and foliations. Enseign. Math. (2), 46(1-2):3–42, 2000.Google Scholar
BCH94.Baum, Paul, Connes, Alain, and Higson, Nigel. Classifying space for proper actions and K-theory of group C*-algebras. In C*-algebras: 1943–1993 (San Antonio, TX, 1993), volume 167 of Contemp. Math., pages 240–291. Amer. Math. Soc., Providence, RI, 1994.Google Scholar
BH04.Benameur, Moulay-Tahar and Heitsch, James L.. Index theory and noncommutative geometry. I. Higher families index theory. K-Theory, 33(2):151–183, 2004.Google Scholar
BN94.Brylinski, J.-L. and Nistor, Victor. Cyclic cohomology of étale groupoids. K-Theory, 8(4):341–365, 1994.CrossRefGoogle Scholar
Bur85.Burghelea, Dan. The cyclic homology of the group rings. Comment. Math. Helv., 60(3):354–365, 1985.CrossRefGoogle Scholar
CH90.Connes, Alain and Higson, Nigel. Déformations, morphismes asymptotiques et K-théorie bivariante. C. R. Acad. Sci. Paris Sér. I Math., 311(2):101–106, 1990.Google Scholar
CM90.Connes, Alain and Moscovici, Henri. Cyclic cohomology, the Novikov conjecture and hyperbolic groups. Topology, 29(3):345–388, 1990.CrossRefGoogle Scholar
CM04.Crainic, Marius and Moerdijk, Ieke. Čech-De Rham theory for leaf spaces of foliations. Math. Ann., 328(1-2):59–85, 2004.Google Scholar
CMR07.Cuntz, Joachim, Meyer, Ralf, and Rosenberg, Jonathan. Topological and Bivariant K-theory, volume 36 of Oberwolfach Seminars. Birkhäuser, Berlin, 2007.Google Scholar
Con79.Connes, Alain. Sur la théorie non commutative de l'intégration. In Algèbres d'opérateurs (Sém., Les Plans-sur-Bex, 1978), volume 725 of Lecture Notes in Math., pages 19–143. Springer, Berlin, 1979.Google Scholar
Con85.Connes, Alain. Noncommutative differential geometry. Inst. Hautes Études Sci. Publ. Math., (62):257–360, 1985.CrossRefGoogle Scholar
Con86.Connes, Alain. Cyclic cohomology and the transverse fundamental class of a foliation. In Geometric methods in operator algebras (Kyoto, 1983), volume 123 of Pitman Res. Notes Math. Ser., pages 52–144. Longman Sci. Tech., Harlow, 1986.Google Scholar
Con94.Connes, Alain. Noncommutative geometry. Academic Press Inc., San Diego, CA, 1994.Google Scholar
CR06.Carrillo-Rouse, Paulo. A Schwartz type algebra for the tangent groupoid. In K-theory and Noncommutative geometry, EMS Series of congress and reports, pages 181–199, 10 2008.CrossRefGoogle Scholar
CR07.Carrillo-Rouse, Paulo. Indices analytiques à support compact pour des groupoides de Lie. Thèse de Doctorat à l'Université de Paris 7, 2007.Google Scholar
Cra99.Crainic, Marius. Cyclic cohomology of étale groupoids: the general case. K-Theory, 17(4):319–362, 1999.CrossRefGoogle Scholar
CS84.Connes, Alain and Skandalis, Georges. The longitudinal index theorem for foliations. Publ. Res. Inst. Math. Sci., 20(6):1139–1183, 1984.CrossRefGoogle Scholar
DLN06.Debord, Claire, Lescure, Jean-Marie, and Nistor, Victor. Groupoids and an index theorem for conical pseudomanifolds. arxiv:math.OA/0609438, 2006.Google Scholar
GL06.Gorokhovsky, Alexander and Lott, John. Local index theory over foliation groupoids. Adv. Math., 204(2):413–447, 2006.CrossRefGoogle Scholar
Goo85.Goodwillie, Thomas G.. Cyclic homology, derivations, and the free loopspace. Topology, 24(2):187–215, 1985.Google Scholar
Gor99.Gorokhovsky, Alexander. Characters of cycles, equivariant characteristic classes and Fredholm modules. Comm. Math. Phys., 208(1):1–23, 1999.CrossRefGoogle Scholar
Hae84.Haefliger, André. Groupoïdes d'holonomie et classifiants. Astérisque, (116):70–97, 1984. Transversal structure of foliations (Toulouse, 1982).Google Scholar
HS87.Hilsum, Michel and Skandalis, Georges. Morphismes K-orientés d'espaces de feuilles et fonctorialité en théorie de Kasparov (d'après une conjecture d'A. Connes). Ann. Sci. École Norm. Sup. (4), 20(3):325–390, 1987.CrossRefGoogle Scholar
Kar78.Karoubi, Max. K-theory. Springer-Verlag, Berlin, 1978. An introduction, Grundlehren der Mathematischen Wissenschaften, Band 226.CrossRefGoogle Scholar
Kar87.Karoubi, Max. Homologie cyclique et K-théorie. Astérisque, (149):147, 1987.Google Scholar
KL05.Kreck, Matthias and Luck, Wolfgang. The Novikov Conjecture, volume 33 of Oberwolfach Seminars. Birkhäuser, Berlin, 2005.CrossRefGoogle Scholar
Lan03.Landsman, N. P.. Quantization and the tangent groupoid. In Operator algebras and mathematical physics (Constanƫa, 2001), pages 251–265. Theta, Bucharest, 2003.Google Scholar
LM89.Lawson, H. Blaine Jr. and Michelsohn, Marie-Louise. Spin geometry, volume 38 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 1989.Google Scholar
LMN00.Lauter, Robert, Monthubert, Bertrand, and Nistor, Victor. Pseudodifferential analysis on continuous family groupoids. Doc. Math., 5:625–655 (electronic), 2000.Google Scholar
Mac87.Mackenzie, K.. Lie groupoids and Lie algebroids in differential geometry, volume 124 of London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge, 1987.Google Scholar
Mel93.Melrose, Richard B.. The Atiyah-Patodi-Singer index theorem, volume 4 of Research Notes in Mathematics. A K Peters Ltd., Wellesley, MA, 1993.CrossRefGoogle Scholar
MN05.Monthubert, Bertrand and Nistor, Victor. A topological index theorem for manifolds with corners. arxiv:math.KT/0507601, 2005.Google Scholar
MP97.Monthubert, Bertrand and Pierrot, François. Indice analytique et groupoïdes de Lie. C. R. Acad. Sci. Paris Sér. I Math., 325(2):193–198, 1997.Google Scholar
NWX99.Nistor, Victor, Weinstein, Alan, and Xu, Ping. Pseudodifferential operators on differential groupoids. Pacific J. Math., 189(1):117–152, 1999.CrossRefGoogle Scholar
Pat99.Paterson, Alan L. T.. Groupoids, inverse semigroups, and their operator algebras, volume 170 of Progress in Mathematics. Birkhäuser Boston Inc., Boston, MA, 1999.Google Scholar
Ren80.Renault, Jean. A groupoid approach to C*-algebras, volume 793 of Lecture Notes in Mathematics. Springer, Berlin, 1980.CrossRefGoogle Scholar
Ros94.Rosenberg, Jonathan. Algebraic K-theory and its applications, volume 147 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1994.CrossRefGoogle Scholar
Sha78.Shanahan, Patrick. The Atiyah-Singer index theorem, volume 638 of Lecture Notes in Mathematics. Springer, Berlin, 1978. An introduction.Google Scholar
Trè80.Trèves, François. Introduction to pseudodifferential and Fourier integral operators. Vol. 1. Plenum Press, New York, 1980. Pseudodifferential operators, The University Series in Mathematics.Google Scholar
Trè06.Trèves, François. Topological vector spaces, distributions and kernels. Dover Publications Inc., Mineola, NY, 2006. Unabridged republication of the 1967 original.Google Scholar
Tu00.Tu, Jean-Louis. The Baum-Connes conjecture for groupoids. In C*-algebras (Münster, 1999), pages 227–242. Springer, Berlin, 2000.Google Scholar