Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T17:17:35.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic K-Theory of ∞-Operads

Published online by Cambridge University Press:  07 November 2014

Thomas Nikolaus
Thomas Nikolaus*
Affiliation:
Fakultät für Mathematik, Universität Regensburg, Universitätsstraße 31, 93053 Regensburg, Germany, [email protected]
Get access

Abstract

The theory of dendroidal sets has been developed to serve as a combinatorial model for homotopy coherent operads, see [MW07, CM13b]. An ∞-operad is a dendroidal set D satisfying certain lifting conditions.

In this paper we give a definition of K-groups Kn (D) for a dendroidal set D. These groups generalize the K-theory of symmetric monoidal (resp. permutative) categories and algebraic K-theory of rings. We establish some useful properties like invariance under the appropriate equivalences and long exact sequences which allow us to compute these groups in some examples. Using results from [Heu11b] and [BN12] we show that the K-theory groups of D can be realized as homotopy groups of a K-theory spectrum .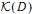

Keywords

Dendroidal setsK-theoryoperadsPrimary: 55U35Secondary:18G30
Type
Research Article
Information
Journal of K-Theory , Volume 14 , Issue 3 , December 2014 , pp. 614 - 641
Copyright
Copyright © ISOPP 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BN12.Bašić, M. and Nikolaus, T.. Dendroidal sets as models for connective spectra. Preprint arxiv:1203.6891, 2012.Google Scholar
BV73.Boardman, J. M. and Vogt, R. M.. Homotopy invariant algebraic structures on topological spaces. Lecture Notes in Mathematics 347. Springer-Verlag, Berlin, 1973.Google Scholar
CM11.Cisinski, D.C. and Moerdijk, I.. Dendroidal sets as models for homotopy operads. J. Topol. 4(4) (2011), 257–299.Google Scholar
CM13a.Cisinski, D.-C. and Moerdijk, I.. Dendroidal Segal spaces and ∞-operads. J. Topol. 6(3) (2013), 675–704.Google Scholar
CM13b.Cisinski, D.-C. and Moerdijk, I.. Dendroidal sets and simplicial operads. J. Topol. 6(3) (2013), 705–756.Google Scholar
Dug01.Dugger, D.. Universal homotopy theories. Adv. Math. 164(1) (2001), 144–176.CrossRefGoogle Scholar
GGN13.Gepner, D., Groth, M., and Nikolaus, T.. Universality of multiplicative infinite loop space machines. Preprint arxiv:1305.4550, 2013.Google Scholar
Heu11a.Heuts, G.. Algebras over infinity-operads. Preprint arxiv: 1110.1776, 2011.Google Scholar
Heu11b.Heuts, G.. An infinite loop space machine for infinity-operads. Preprint arxiv: 1112.0625, 2011.Google Scholar
Lur09.Lurie, J.. Higher topos theory. Annals of Mathematics Studies. Princeton University Press, 2009.Google Scholar
Lur12.Lurie, J.. Higher algebra. Prepublication book draft, available at http://www.math.harvard.edu/~lurie/, 2012.Google Scholar
May74.May, J.P.. E ∞ spaces, group completions, and permutative categories. New developments in topology (Proc. Sympos. Algebraic Topology, Oxford, 1972) 11 (1974), 61–93.Google Scholar
May77.May, J.P.. Infinite loop space theory. Bull. Amer. Math. Soc 83(4) (1977), 456–494.Google Scholar
May99.May, J.P.. A concise course in algebraic topology. University of Chicago Press, 1999.Google Scholar
MSS02.Markl, M., Shnider, S., and Stasheff, J.. Operads in algebra, topology and physics, Mathematical Surveys and Monographs 96. American Mathematical Society, 2002.Google Scholar
MT78.May, J.P. and Thomason, R.. The uniqueness of infinite loop space machines. Topology 17(3) (1978), 205–224.Google Scholar
MW07.Moerdijk, I. and Weiss, I.. Dendroidal sets. Algebr. Geom. Topol. 7 (2007), 1441–1470.Google Scholar
MW09.Moerdijk, I. and Weiss, I.. On inner Kan complexes in the category of dendroidal sets. Adv. Math. 221(2) (2009), 343–389.CrossRefGoogle Scholar
Nik11.Nikolaus, T.. Algebraic models for higher categories. Indag. Math. (N.S.) 21(1-2) (2011), 52–75.Google Scholar
Qui73.Quillen, D.. Higher algebraic K-theory. I. In Algebraic K-theory, I: Higher K -theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pages 85–147. Lecture Notes in Math. 341. Springer, Berlin, 1973.Google Scholar
Tho82.Thomason, R.W.. First quadrant spectral sequences in algebraic K-theory via homotopy colimits. Comm. Algebra 10(15) (1982), 1589–1668.CrossRefGoogle Scholar