Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T06:11:28.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Tangent bundle of hypersurfaces in G/P

Published online by Cambridge University Press:  12 May 2008

Indranil Biswas  and
Georg Schumacher
Indranil Biswas
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005, India, [email protected].
Georg Schumacher
Affiliation:
Fachbereich Mathematik und Informatik, Philipps-Universität Marburg, Lahnberge, Hans-Meerwein-Strasse, D-35032 Marburg, Germany, [email protected].
Get access

Abstract

Let G be a simple linear algebraic group defined over an algebraically closed field k of characteristic p ≥ 0, and let P be a maximal proper parabolic subgroup of G. If p > 0, then we will assume that dimG/P ≤ p. Let ι : H ↪ G/P be a reduced smooth hypersurface in G/P of degree d. We will assume that the pullback homomorphism 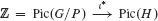is an isomorphism (this assumption is automatically satisfied when dimH ≥ 3). We prove that the tangent bundle of H is stable if the two conditions τ(G/P) ≠ d and 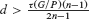hold; here n = dimH, and τ(G/P) ∈ 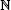is the index of G/P which is defined by the identity 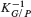= 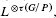where L is the ample generator of Pic(G/P) and 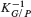is the anti–canonical line bundle of G/P. If d = τ(G/P), then the tangent bundle TH is proved to be semistable. If p > 0, and 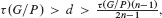then TH is strongly stable. If p > 0, and d = τ(G/P), then TH is strongly semistable.

Keywords

Homogeneous spacehypersurfacestable tangent bundle
Type
Research Article
Information
Journal of K-Theory , Volume 4 , Issue 1 , August 2009 , pp. 91 - 100
Copyright
Copyright © ISOPP 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Biswas, I.: On the stability of homogeneous vector bundles, Jour. Math. Sci. Univ. Tokyo 11 (2004), 133–140Google Scholar
2.Deligne, P. and Illusie, L.: Relèvements modulo p 2 et décomposition du complexe de de Rham, Invent. Math. 89 (1987), 247–270CrossRefGoogle Scholar
3.Griffiths, P. and Harris, J.: Principles of Algebraic Geometry, John Wiley & Sons Inc., New York, 1978Google Scholar
4.Grothendieck, A.: Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Advanced Studies in Pure Mathematics 2, North-Holland Publishing Co., Amsterdam; Masson & Cie, Éditeur, Paris, 1968Google Scholar
5.Kobayashi, S.: Differential Geometry of Complex Vector Bundles, Publications of the Math. Society of Japan 15, Iwanami Shoten Publishers and Princeton University Press, 1987Google Scholar
6.Kobayashi, S. and Ochiai, T.: On complex manifolds with positive tangent bundles, Jour. Math. Soc. Japan 22 (1970), 499–525Google Scholar
7.Kollár, J.: Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete 3 Folge 32, Springer-Verlag, Berlin, (1995)Google Scholar
8.Mehta, V. B. and Ramanathan, A.: Homogeneous bundles in characteristic p, (in: Algebraic geometry—open problems (Ravello, 1982)), 315–320, Lecture Notes in Math. 997, Springer, Berlin, 1983.Google Scholar
9.Ramanan, S. and Ramanathan, A.: Some remarks on the instability flag, Tôhoku Math. Jour. 36 (1984), 269–291Google Scholar
10.Umemura, H.: On a theorem of Ramanan, Nagoya Math. Jour. 69 (1978), 131–138CrossRefGoogle Scholar