Introduction
The informal economy, defined as all market-based legal production of goods and services deliberately concealed from public authorities to avoid payment of taxes or social security contributions or meeting specific legal labour market standards (Schneider et al., Reference Schneider, Buehn and Montenegro2010), is a global phenomenon. With the informal economy representing, on average, 35% of GDP in low- and middle-income countries, economists and policymakers widely agree that a high share of the informal economy hinders the achievement of various desirable economic outcomes (La Porta and Shleifer, Reference La Porta and Shleifer2014; Schneider, Reference Schneider2005).
Could the objective of shrinking the informal economy be impeded by the insistence of international economic organisations on reducing the size of the public sector? Since the 1980s, these organisations have been focusing on the size of the public sector as a problem that needs to be addressed.Footnote 1 The combination of the international debt and fiscal crises afflicting many developing countries in the 1980s cemented policymakers’ opinion regarding the need to shrink bloated bureaucracies and cut public-sector pay (Rodrik, Reference Rodrik2000). That was, to some extent, a response to the rapid increase in the size of government consumption and public-sector employment in developing economies of the previous decades, as well as disaffection with the perceived inefficiencies and low-growth prospects engendered by state-led development strategies (Rama, Reference Rama1999).
Given the need for public-sector employment retrenchment, this paper examines the influence of prescribed public-sector employment cuts on the size of the informal sector. In other words, we inquire whether public-sector employment retrenchment may be incompatible with the goal of shrinking the informal economy. To our knowledge, this is the first paper that examines this relationship.
In the empirical section of the paper, we show that a public-sector employment reduction programme exerts a positive and statistically significant effect on the shadow economy’s share of GDP. This increase persists for at least 5 years after the programme began, reaching 1.3 percentage points of GDP. Moreover, the identified effect is more pronounced in autocracies and countries with low institutional quality. In these countries, the informal rather than the formal sector can easily absorb excess workers. Hence, much of the reallocation of workers from public-sector layoffs will end up in the shadow economy. This finding supports the view that low institutional quality hampers economic adjustment and development by channelling workers towards low-productivity activities.
To estimate our main empirical relationship, we use quasi-experimental data provided by policy-induced public-sector dismissal programmes introduced by all International Monetary Fund (IMF) conditionality programmes from 1990 to 2018. The main empirical challenge, then, is to estimate the causal effect of the public-sector employment reduction programme on the share of the shadow economy, given that IMF conditionality programmes are non-random events. In particular, macroeconomic, structural, and political factors determine the probability that a public-sector employment cutback is included as a condition of an IMF programme. Similarly, one may think that countries with a higher share of the shadow economy will have a higher propensity to face macroeconomic turbulence after an exogenous shock and thus resort to IMF for emergency lending. To deal with both issues, we use the dynamic Augmented Inverse Probability Weighting Regression Adjustment (Angrist et al., Reference Angrist, Jordi and Kuersteiner2018; Jordà and Taylor, Reference Jordà and Taylor2016). This method creates pseudo-randomisation by first estimating the propensity of having a public-sector employment reduction programme and then rebalancing the sample so that observations with higher (lower) propensity receive lower (higher) weighting.
Then, as a next step, to explain our empirical findings, we build a simple theoretical model that captures the reallocation of economic activity between the formal and informal economy in response to government employment cuts. This model provides our underlying rationale behind the shift of economic activity from the public to the private informal rather than formal sector. The main reason for this effect is that public-sector layoffs have two effects. First, they increase the supply of labour in the private sector (formal and informal). This results in higher production in both the informal and formal sectors. At the same time, this increase in labour supply reduces wages and incomes, driving a switch in demand from high-quality products (produced in the formal sector) to low-quality goods produced in the informal sector. Consequently, the informal sector expands at the expense of the formal sector.
An important institutional factor that may impede or facilitate the reallocation towards the informal sector is the quality of the institutional environment. In countries with low government effectiveness, high corruption, and weak rule of law, it is expected that the expansion of the informal sector will be relatively unhindered, implying that public-sector layoffs will result in a higher increase in the share of the shadow economy relative to countries in which it is more difficult to bypass the existing labour (and product) market regulations. Our empirical results show that this is indeed the case. This is consistent with the extensive literature highlighting the role of formal and informal institutions on the size of the shadow economy (see, e.g. Gërxhani and Cichocki, Reference Gërxhani and Cichocki2023; Johnson et al., Reference Johnson, Kaufmann and Zoido-Lobaton1998).
Our findings are related to recent literature that examines the effect of IMF programmes on the economy. Even though most of the early contributions examined the impact of IMF programmes on growth (see Balima and Sokolova, Reference Balima and Sokolova2021), recent studies focus on the implications for specific policy areas and economic outcomes (see, e.g. Dreher et al., Reference Dreher, Sturm and Vreeland2015; Lang, Reference Lang2021). For example, Blanton et al. (Reference Blanton, Early and Peksen2018) show that participation in an IMF structural adjustment programme can lead to higher shadow sector activity as IMF-imposed structural conditions reduce growth and degrade the states’ regulatory capacity. In contrast to these studies, our econometric framework allows us to emphasise the IMF programmes’ causal effect and the dynamics of the underlying relationship. Moreover, our results differ from those of these previous studies, as we show that it is not the IMF programmes, per se, that increase the size of the shadow economy; instead, the conditions for public-sector employment reductions induce a sectoral shift towards the shadow economy.
Our paper is also related to the literature examining the informal sector’s size determinants. Several authors (e.g. Gërxhani and Cichocki, Reference Gërxhani and Cichocki2023; Khan and Rehman, Reference Khan and Rehman2022; Schneider and Enste, Reference Schneider and Enste2000) emphasise the role of formal and informal institutions, as well as of government policies, in the size of the shadow economy. Consistent with these studies, we show that institutions also indirectly shape the economy’s structure by influencing how policies affect the demand and supply of the informal sector. Thus, our work is related to studies that find that government policies drive the growth in the shadow economy and how the institutional environment mediates this effect. Our empirical findings also support the view that informality may be demand-driven; that is, households turn to the informal sector when they face limited employment opportunities (Pham, Reference Pham2022).
The rest of the paper is organised as follows: Section 2 presents the empirical model and discusses the results of our investigation, while Section 3 develops a theoretical framework that can explain our findings. The last section offers concluding comments.
Empirical analysis
Data and empirical model
The main goal is to estimate the effect of dismissals of public-sector employees on the shadow economy. To this end, we exploit the impact of policy-induced public-sector dismissals introduced by IMF conditionality programmes. Typically, IMF programmes include several conditions regarding the size of public-sector employment. Once a country borrows from the IMF, its government agrees to initiate a series of reforms to correct the underlying inefficiencies of its economy. Programme conditions focus on macroeconomic, financial, and monetary issues; however, several programmes include structural reforms in areas like the labour and product market. In this respect, one condition typically included in several programmes is reducing public-sector employment or the total public-sector wage bill. Besides improving government finances, this condition is expected to affect the wage and employment structure in the labour market (Adam, Reference Adam2020; Malley and Moutos, Reference Malley and Moutos1996). According to the database of IMF conditionality (Kentikelenis et al., Reference Kentikelenis, Stubbs and King2016), in the period from 1990 to 2018, out of the 185 total IMF programmes initiated in all countries, only 42 programmes involved a condition to reduce the number of civil servants, whereas 48 programmes had a policy prescription of lowering the total public-sector wage bill.Footnote 2
To estimate the effect of public-sector dismissal, we develop a dynamic model in the spirit of Angrist et al. (Reference Angrist, Jordi and Kuersteiner2018), Jordà and Taylor (Reference Jordà and Taylor2016), and Kuvshinov and Zimmermann (Reference Kuvshinov and Zimmermann2019). More specifically, we compare the change in the share of the shadow economy from year 0, that is, 1 year before a programme that involved reductions in public-sector employment, to year h = 1,2,3,4,5. As the control group, we use all countries under an IMF programme. However, IMF programmes are non-random policy events; therefore, we use the inverse probability weighting method to mimic randomisation.Footnote 3
This method has a series of advantages. First, it estimates the dynamic effect of IMF public-sector employment reduction programmes on the outcome variable. Second, it allows for non-linearities in the time response of the outcome (i.e. the share of the shadow economy) to the treatment (i.e. public-sector employment reductions). Third, we extend the empirical model to allow for the local projection of the shadow economy by estimating a two-stage model that relies on the inverse probability weighting and the regression adjustment method (Jordà et al., Reference Jordà, Schularick and Taylor2016; Jordà and Taylor, Reference Jordà and Taylor2016). This latter model has the significant advantage that it requires only one of both stages, ordinary least squares (OLS) or probit, to be correctly specified to derive correct estimates for the effect of treatment, that is, public-sector layoff programmes. In addition, neither method relies on any exclusion restrictions, and thus, all variables can be considered endogenous in our dataset (Kuvshinov and Zimmermann, Reference Kuvshinov and Zimmermann2019). As a result, our analysis effectively takes into account the endogeneity.
To be more specific, we assume that the following probit model gives the estimated probability of having an IMF programme that reduces public-sector employment:
 $$\widehat {P{V_{i,t}}} = \Phi \left( {\mathop \sum \limits_{j = 1}^2 {S_{i,t - j}},{X_{i,t}},\, \hat {\!\beta} } \right)$$
$$\widehat {P{V_{i,t}}} = \Phi \left( {\mathop \sum \limits_{j = 1}^2 {S_{i,t - j}},{X_{i,t}},\, \hat {\!\beta} } \right)$$
where
![]() $\widehat {P{V_{i,t}}}$
is the predicted probability of a public-sector employment reduction programme in country i at time t + 1,
$\widehat {P{V_{i,t}}}$
is the predicted probability of a public-sector employment reduction programme in country i at time t + 1,
![]() $\Phi $
is the cumulative distribution function of the standard normal distribution,
$\Phi $
is the cumulative distribution function of the standard normal distribution,
![]() ${S_{i,t - j}}$
is the lagged value of shadow economy as a share of GDP at j years before the programme is enacted,
${S_{i,t - j}}$
is the lagged value of shadow economy as a share of GDP at j years before the programme is enacted,
![]() ${X_{i,t}}$
is a vector of control variables, and finally,
${X_{i,t}}$
is a vector of control variables, and finally,
![]() ${\hat {\!\beta}} $
is the vector of estimated coefficients.Footnote
4
Then, the average treatment effect (ATE) of the treatment for each h, that is, public-sector employment reduction under the Augmented Inverse Probability Weighting Scheme, is given by
${\hat {\!\beta}} $
is the vector of estimated coefficients.Footnote
4
Then, the average treatment effect (ATE) of the treatment for each h, that is, public-sector employment reduction under the Augmented Inverse Probability Weighting Scheme, is given by
 $$\eqalign{ \Lambda _{AIPW}^h = & {1 \over n}\sum\limits_i {\sum\limits_t {\left\{ {\left[ {{{{D_{i,t}}\left( {{S_{i,t + h}} - {S_{i,t}}} \right)} \over {\widehat {P{V_{i,t}}}}} - {{(1 - {D_{i,t}})\left( {{S_{i,t + h}} - {S_{i,t}}} \right)} \over {\widehat {1 - P{V_{i,t}}}}}} \right]\;} + \left[ {m_1^h\left( {X_{i,t}^{},\hat \theta _1^h} \right) - m_0^h\left( {X_{i,t}^{},\hat \theta _0^h} \right)} \right]\right.}} \cr & - \left[ {{{{D_{i,t}}m_1^h\left( {X_{i,t}^{},\hat \theta _1^h} \right)} \over {\widehat {P{V_{i,t}}}}} - {{(1 - {D_{i,t}})m_0^h\left( {X_{i,t}^{},\hat \theta _0^h} \right)} \over {\widehat {1 - P{V_{i,t}}}}}} \right] \Bigg\} }$$
$$\eqalign{ \Lambda _{AIPW}^h = & {1 \over n}\sum\limits_i {\sum\limits_t {\left\{ {\left[ {{{{D_{i,t}}\left( {{S_{i,t + h}} - {S_{i,t}}} \right)} \over {\widehat {P{V_{i,t}}}}} - {{(1 - {D_{i,t}})\left( {{S_{i,t + h}} - {S_{i,t}}} \right)} \over {\widehat {1 - P{V_{i,t}}}}}} \right]\;} + \left[ {m_1^h\left( {X_{i,t}^{},\hat \theta _1^h} \right) - m_0^h\left( {X_{i,t}^{},\hat \theta _0^h} \right)} \right]\right.}} \cr & - \left[ {{{{D_{i,t}}m_1^h\left( {X_{i,t}^{},\hat \theta _1^h} \right)} \over {\widehat {P{V_{i,t}}}}} - {{(1 - {D_{i,t}})m_0^h\left( {X_{i,t}^{},\hat \theta _0^h} \right)} \over {\widehat {1 - P{V_{i,t}}}}}} \right] \Bigg\} }$$
where
![]() ${\rm{m}}_1^{\rm{h}}\left( {{\rm{X}}_{{\rm{i}},{\rm{t}}}^{},{\rm{\hat \theta }}_1^{\rm{h}}} \right)\;{\rm{and}}\;{\rm{m}}_0^{\rm{h}}\left( {{\rm{X}}_{{\rm{i}},{\rm{t}}}^{},{\rm{\hat \theta }}_0^{\rm{h}}} \right)$
are the conditional mean of a regression of
${\rm{m}}_1^{\rm{h}}\left( {{\rm{X}}_{{\rm{i}},{\rm{t}}}^{},{\rm{\hat \theta }}_1^{\rm{h}}} \right)\;{\rm{and}}\;{\rm{m}}_0^{\rm{h}}\left( {{\rm{X}}_{{\rm{i}},{\rm{t}}}^{},{\rm{\hat \theta }}_0^{\rm{h}}} \right)$
are the conditional mean of a regression of
![]() $\left( {{{\rm{S}}_{{\rm{i}},{\rm{t}} + {\rm{h}}}} - {{\rm{S}}_{{\rm{i}},{\rm{t}}}}} \right)$
on
$\left( {{{\rm{S}}_{{\rm{i}},{\rm{t}} + {\rm{h}}}} - {{\rm{S}}_{{\rm{i}},{\rm{t}}}}} \right)$
on
![]() $X_{i,t}^{}$
and
$X_{i,t}^{}$
and
![]() ${{\rm{D}}_{{\rm{i}},{\rm{t}}}}$
is the dummy that separates the treatment and control group.
${{\rm{D}}_{{\rm{i}},{\rm{t}}}}$
is the dummy that separates the treatment and control group.
Note that (2) is estimated for each time horizon h=1,…, 5; thus, we compute the change in the share of the shadow economy for each period h after the treatment.Footnote 5 Then, for each period after that, we examine the associated change compared to the value at t. We follow Jordà and Taylor (Reference Jordà and Taylor2016) and use cluster robust methods to compute the estimated coefficients’ standard errors.
To measure the size of the shadow economy, we use the dynamic general equilibrium (DGE) estimates of the share of the shadow economy of Elgin et al. (Reference Elgin, Kose, Ohnsorge and Yu2021). The main advantage of this method is that it covers a wide range of countries over a considerable period. In the present paper, we use the available estimates for our sample of countries over the 1990–2018 period. To ensure that our results are not driven by the choice of the DGE model estimates, for robustness, we also use the Multiple Indicators Multiple Causes (MIMIC) model-based estimates provided by the same authors.Footnote 6
Vector X i,t includes a series of macroeconomic controls to model the selection into treatment. These are the current account balance as a share of GDP, the government budget balance as a share of GDP, a dummy that takes the value of 1 when a country is a democracy, the log of GDP per capita, the growth rate of GDP per capita, the number of years that the country has spent under an IMF programme, the unemployment rate, the degree of public-sector corruption, the share of the urban population, and finally, the labour force participation rate.Footnote 7
Results
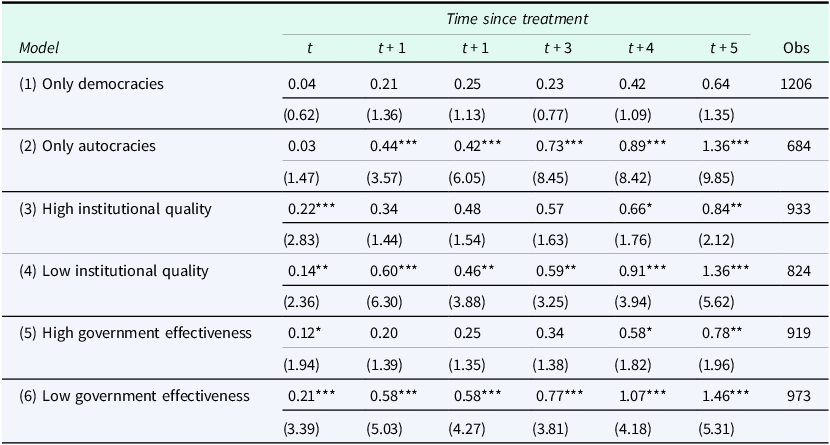
The main results are presented in Table 1. Each line presents a different model specification of the main model described in equations (1) and (2). Then, each column is the ATE at time t + h. Clustered t-statistics are presented in parentheses.
Table 1. Main results and robustness

Notes: The table presents the average treatment effect (ATE) of a public-sector employment reduction programme in 105 countries from 1990 to 2018. Each line in the table corresponds to a different specification for the model described in equations (1) and (2). Each corresponding column gives the ATE at time t + h after implementing the public-sector employment reduction programme. The outcome variable in all but the last model is the share of the shadow economy to total GDP (dynamic general equilibrium model estimates except model 2, where the shares are obtained by a Multiple Indicators Multiple Causes (MIMIC) model). The outcome variable in model (8) is the government spending to GDP ratio. Clustered robust, t-statistics in parentheses. *, **, *** denote statistical significance at the 10%, 5%, and 1% level of statistical significance, respectively.
According to the first model of Table 1, a public-sector dismissal programme, that is, a programme that postulates that the government should reduce the share of public-sector employment or reduce the public-sector wage bill, has a positive and statistically significant effect on the share of the shadow economy. Moreover, moving across columns, we can establish that the estimated effect increases over time, reaching a 1.3 percentage point increase in the share of the shadow economy at t + 5, that is, after 5 years.Footnote 8 Figure 1 provides a visual representation of the estimated effect for 5 years after treatment, together with the 5% (dark grey) and 10% (light grey) confidence intervals.

Figure 1. The effect of public-sector employment reduction on the shadow economy.
The rest of the models in Table 1 correspond to several robustness tests. In the second model, we use the estimates of the shadow economy as in Medina and Schneider (Reference Medina and Schneider2017). The Medina and Schneider data use the MIMIC approach to measure the size of the shadow economy. The estimated effect is very close to the one obtained in the first model, suggesting that the underlying measure of the shadow economy does not drive our results.Footnote 9
In model (3), we re-estimate the same equation when we consider only IMF programmes with public-sector layoffs instead of including programmes with provisions for public-sector wage bill reductions. As we explain in the theoretical section, we expect the effect for both types of programmes to be similar. The results in model (3) verify the positive impact of IMF public-sector layoffs on the share of the shadow economy.
In the rest of the lines in Table 1, we examine whether our results hold under various empirical model specifications. Specifically, we first estimate (1) and (2) using only lagged values of the dependent variable and dropping all the rest of the covariates. Next, in models (5) and (6), we experiment with the lag length of the dependent variable. Finally, in model (7), we estimate the main model, excluding the fixed effects from the regression adjustment model. In all cases, the qualitative nature of our results remains, and the estimated effects are very close to the baseline case, that is, model 1.
It bears noting that our finding that a programme involving public-sector layoffs induces an increase in the share of the shadow economy in aggregate economic activity could be just a purely mechanical implication of the reduction in the (absolute) size of the government sector; since the government sector is part of the official economy, a reduction in its size would produce a rise in the share of the shadow economy even if there was no change in the absolute size of the shadow economy. To remedy this and to examine whether our results correspond to a structural change in the economy involving the reallocation of private economic activity between the formal and informal sectors, in the final line of Table 1, we examine the impact of public-sector layoffs on the evolution of the share of government spending in GDP. We find that a public-sector employment reduction programme does not negatively affect the relative size of the public sector. In fact, after the initial decline in the share of government spending, we observe a reversal in the following period and a non-significant impact from the period t + 2 onwards.Footnote 10
Thus, despite the initial fall in the share of government spending in GDP, the share of government spending returns to its initial value after 2 years. Given that, in our sample, the average share of government spending in GDP is about 30% and that the average share of the shadow economy is about 35% of GDP, we can approximateFootnote 11 the share of the formal private sector to be (the remaining) 35% of GDP. These imply that the size of the formal private sector relative to the size of the informal sector is equal to 1. Following the public-sector layoffs, we find that the share of government remains at 30% of GDP (Model 8 of Table 1). In contrast, the share of the shadow economy expands by 1.3% percentage points (model 1 of Table 1) to 36.3% of GDP. This implies that after the public-sector layoffs, there was a reduction in the share of the formal private sector to 33.7% of GDP. Thus, the size of the formal private sector relative to the size of the informal sector becomes now equal to 0.93 (=33.7/36.3), therefore involving a sizable reallocation of private economic activity from its formal to its informal part of about seven percentage points (from 1 to 0.93).Footnote 12
In Table 2, we perform a series of additional robustness tests. First, we examine whether the derived result is the outcome of the layoff conditions or whether all IMF programmes increase the shadow economy’s share. Even though we do not have specific priors for all IMF programmes, our theoretical hypothesis suggests that programmes that include public-sector layoff conditions must increase the shadow economy’s share. Hence, in model (1), we use the occurrence of any IMF programme as the treatment variable. Our results indicate that not all IMF programmes result in a statistically significant increase in the share of the shadow economy.Footnote 13
Table 2. Additional robustness tests

Notes: The outcome variable is always the share of the shadow economy to total GDP. See also Table 1.
Then, in model (2), we perform a placebo test to determine whether we have derived a true effect. More specifically, we randomise the treatment variable to create a fake treatment with randomised treatment units and times by always considering the staggered adoption of our ‘real’ variable. We perform this randomisation and estimate the main model 200 times. The means of these estimates are presented in the table, with their corresponding t-statistic. As this exercise shows, the mean random treatment gives, on average, a negative effect of the treatment variable on the share of the shadow economy, rejecting the hypothesis of a placebo effect.
As a final robustness test, in the rest of Table 2, we exclude one country group at a time. In this way, we examine whether specific country groups drive our results. Except for when we exclude Africa, the rest of the results indicate no statistically significant difference with the baseline case. When we exclude Africa, the statistical significance of the results remains; however, the estimated ATEs drop in magnitude. This is an interesting result that motivates the analysis of the following subsection. Most countries in Africa have low institutional quality. Hence, excluding these countries from the sample increases the share of countries with high institutional quality. The results are then suggestive of a heterogeneity depending on the level of institutional quality: the postulated impact of public-sector layoffs on the share of the shadow economy may be more pronounced in countries with low institutional quality. We examine this in the following subsection.
The role of institutions
An extensive literature on the determinants of the size of the informal sector shows the importance of institutions (Gërxhani and Cichocki, Reference Gërxhani and Cichocki2023; Khan and Rehman, Reference Khan and Rehman2022). When institutional quality and government efficiency are low, we expect it will be easier for unemployed workers to find a job in the shadow economy.
In Table 3, we examine the role of institutions regarding the effect of policy-induced public-sector layoffs on the share of the shadow economy. All results are obtained using the first model of Table 1 as the baseline case. First, we examine the underlying relationship depending on the level of institutional quality since political and economic institutions are expected to influence the ease with which workers and firms can relocate between the formal and informal sectors. In economies with a weak institutional environment, the expansion of the informal sector will be largely unhindered; thus, we should expect a higher reallocation towards the shadow economy compared to countries with a better institutional environment. We expect that a similar rationale will also apply if one differentiates countries according to political regimes since in authoritarian political systems, institutions such as the tax authorities, various regulatory bodies, the judiciary, and law enforcement are mere instruments of autocratic rule, without the autonomy required to be effective guardians of compliance with existing laws and regulations.
The results in the first four models of Table 3 indicate this is the case. First, we differentiate between democratic and autocratic countries using the dichotomous democracy variable (Bjørnskov and Rode, Reference Bjørnskov and Rode2020). The positive effect of public-sector layoffs on the share of the shadow economy is more pronounced in autocracies, where all effects are statistically significant for all years after the programme’s initiation. Furthermore, the point estimates are more than double in magnitude than in the case of democracies. Moreover, as the first line indicates, the ATEs for democracies are much lower in size and statistically significant only for 4 and 5 years after treatment.
A similar picture emerges when we split our sample into countries with high and low institutional quality. A country is classified as one of high (low) institutional quality when the International Country Risk Guide indicator of Quality of Government (taken from Teorell et al., Reference Teorell, Dahlberg, Holmberg, Rothstein, Alvarado Pachon and Axelsson2020) is above (below) the variable’s median value. The results indicate that the effect of public-sector employment reductions is more pronounced in countries with low institutional quality. All point estimates, except for time t when they are statistically the same, are more than twice in magnitude in countries with low institutional quality.
Finally, in models (5) and (6), we replicate the same analysis regarding the effect of institutions as in models (3) and (4); however, this time, we use the government effectiveness index (as taken from the World Bank Governance Indicators). Countries with higher government efficiency are expected to be able to limit the size of the shadow economy. Thus, we should expect that policy-induced public-sector layoffs will not result in many workers ending up in the shadow economy as the government will control the expansion of the informal sector. Countries are classified as ones with high (low) government effectiveness if the average government effectiveness index is above (below) the (sample) median value. The results in models (5) and (6) replicate the results obtained so far.
Overall, the empirical results show a robust positive, non-mechanical relationship between public-sector dismissal programmes and the size of the shadow economy. Moreover, this relationship appears to persist over time; thus, it is not due to a temporary adjustment process until the laid-off workers find a job in the formal sector but suggests a change in the economy’s structure. Countries with a low-institutional-quality environment, where shifting to the unregulated informal sector is easier, are more prone to this change.
A theoretical framework
In this section, we provide a theoretical framework to explain the main findings of our empirical analysis. We consider the case of an economy consisting of two perfectly competitive sectors. One produces a homogeneous good, and the other produces a vertically differentiated product. We identify the homogeneous-good sector with agriculture and assume that its output is produced by informal firms only. The production of the vertically differentiated product (VDP) is segmented according to quality: high-quality varieties are produced by formal firms (indexed by F), whereas low-quality varieties are produced by informal firms (indexed by IN). This assumption is based on the ‘quality dualism’ framework of Banerji and Jain (Reference Banerji and Jain2007): in many developing countries, while informal firms produce goods and services that formal firms also produce, there is a quality gap between the outputs of the two sectors, with formal firms having a comparative advantage in high-quality varieties and informal firms in low-quality substitutes.Footnote 14
For ease of exposition, we refer to the sector producing the VDP as the modern sector and the agricultural sector as the agrarian sector. We will reserve the adjective ‘informal’ only for (that subset of) modern-sector firms, with the understanding that all producers in the agrarian sector are informal.
Sectoral specification
Agrarian sector
The agrarian good is produced using informal labour and a factor in fixed supply. The factor in fixed supply is provided by landowners (land), and we normalise its supply to unity. The labour used by the agrarian sector is denoted by L A.
The agrarian sector’s production function displays diminishing returns:
where A denotes output, with both
![]() $\gamma$
and
$\gamma$
and
![]() $\delta $
positive.
$\delta $
positive.
Denoting the (informal) wage rate as
![]() $w$
, and using the agrarian good as the numeraire (P
A
=1), the sector’s profit-maximising demand for labour is
$w$
, and using the agrarian good as the numeraire (P
A
=1), the sector’s profit-maximising demand for labour is
The resulting aggregate profits of agrarian sector producers are equal to
We assume that profits are equally distributed among the landowners, whose number equals T.
The modern sector
The modern sector comprises two distinct sub-sectors: the formal sector and the informal sector. What distinguishes the two sectors is that the formal sector produces a high-quality variety of the VDP, whereas the informal sector produces a low-quality variety. The VDP is produced only with labour. Quality is measured by an index
![]() $Q,$
$Q,$
![]() $0 \lt Q \lt 1$
, and there is complete information regarding the quality index. We assume that there exists a ‘cottage’ technology available to all for producing low-quality varieties of the VDP and a modern technology allowing the production of high-quality varieties. Low-quality varieties are defined as those for which
$0 \lt Q \lt 1$
, and there is complete information regarding the quality index. We assume that there exists a ‘cottage’ technology available to all for producing low-quality varieties of the VDP and a modern technology allowing the production of high-quality varieties. Low-quality varieties are defined as those for which
![]() $Q \lt \bar Q$
, whereas high-quality varieties are identified with
$Q \lt \bar Q$
, whereas high-quality varieties are identified with
![]() $Q \gt \bar Q$
. Firms with access to the technology that allows the production of high-quality varieties belong to the formal sector, whereas the rest are informal. We may think that production technology is such that formal firms have access to excludable public inputs, allowing them to produce high-quality goods at a lower cost than informal firms (e.g. access to electricity at subsidised prices). Moreover, this categorisation of firms is motivated by the fact that consumers of high-quality, high-priced items are more likely to demand after-sales services (guarantees, repairs, etc.) to which only formal sector firms can credibly commit to (and be legally responsible).
$Q \gt \bar Q$
. Firms with access to the technology that allows the production of high-quality varieties belong to the formal sector, whereas the rest are informal. We may think that production technology is such that formal firms have access to excludable public inputs, allowing them to produce high-quality goods at a lower cost than informal firms (e.g. access to electricity at subsidised prices). Moreover, this categorisation of firms is motivated by the fact that consumers of high-quality, high-priced items are more likely to demand after-sales services (guarantees, repairs, etc.) to which only formal sector firms can credibly commit to (and be legally responsible).
For informal firms to be able to produce the low-quality variety at a lower cost than formal firms, we need to assume that the difference in productivity between formal and informal producers is small when quality is low – since then, any wage advantage of informal firms (explained below) could offset their productivity disadvantage (see Fotoniata and Moutos (Reference Fotoniata and Moutos2013) for applications of this idea in other contexts). Rauch (Reference Rauch1991) suggested that the inferior technological capability of informal firms is the reason for their inability to compete on an equal footing with formal firms, thus forcing them to operate in the informal sector where the ability to avoid some costs related to regulation allows them to survive. Our assumption that modern technology is available to a subset of firms that hire only formal workers is used as a convenient shortcut to concentrate on the implications of the interactions between the structure of product demand, the informal sector, and government employment.
As long as the informal producers’ productivity disadvantage gets larger as quality increases, there will be a quality threshold after which formal producers will have lower costs than informal ones. Our assumption that modern technology is available only to a subset of firms starkly manifests this idea.
This simple formulation captures two fundamental features of a typical dual developing economy: (1) the quality gap between sectors and (2) the limited access of the informal sector to public services.
Formal firms face labour market regulation in having to pay a (binding) minimum wage,
![]() $\overline w$
. In addition to labour market regulations, formal firms have to incur a cost, F, per physical unit of output. We may consider this cost the ‘price of formality,’ representing the burden of various taxesFootnote
15
imposed on formal firms or the costs of complying with various environmental, health, or work-safety regulations. Informal firms do not comply with any of the above regulations and pay their workers the (market-clearing) informal wage rate
$\overline w$
. In addition to labour market regulations, formal firms have to incur a cost, F, per physical unit of output. We may consider this cost the ‘price of formality,’ representing the burden of various taxesFootnote
15
imposed on formal firms or the costs of complying with various environmental, health, or work-safety regulations. Informal firms do not comply with any of the above regulations and pay their workers the (market-clearing) informal wage rate
![]() $w$
. We assume that the minimum-wage rate,
$w$
. We assume that the minimum-wage rate,
![]() $\overline w$
, is higher than the informal wage rate,
$\overline w$
, is higher than the informal wage rate,
![]() $w \lt \overline w$
.
$w \lt \overline w$
.
Following Flam and Helpman (Reference Flam and Helpman1987) and Banerji and Jain (Reference Banerji and Jain2007), we assume that average costs depend on quality and that, for any given quality level, average cost is independent of the number of physical units produced. Perfect competition ensures that prices will equal average (and marginal) costs. We write the average cost functions (as functions of quality) for formal and informal firms as,
Since
![]() $\overline w \gt w\;$
and
$\overline w \gt w\;$
and
![]() ${Q_F} \gt {Q_I}$
, it follows that the price of formal firms will be higher than of informal firms:
${Q_F} \gt {Q_I}$
, it follows that the price of formal firms will be higher than of informal firms:
This specification of average costs implies that as quality increases, more units of labour are required to produce each physical unit of the VDP product. This assumption is consistent with the fact that increases in quality – for a given state of technological capability – involve the employment of a larger number of personnel not only for the production of a higher number of features attached to each good that directly absorb labour but also to the development and refinement of these features as well.
Households
The economy is populated by a fixed number of landowners (T) and identical working households (L), each endowed with one unit of labour, which they offer inelastically. For simplicity, we assume that the landowning households do not supply any labour.
Following Flam and Helpman (Reference Flam and Helpman1987), we treat the homogeneous good as divisible, while the VDP is assumed to be indivisible, and households can consume only one unit of it. A convenient characterisation of household preferences over the consumption of goods (for either landowners or working households) is given by the following utility function for household i:
In equation (8), Q stands for the quality (either Q
F
or Q
I
) level of the VDP,
![]() ${A_i}$
is the quantity of the homogeneous good (agricultural) consumed by agent i, and θ
i
is a parameter that differentiates the intensity of household preferences for the quality level of the VDP.
${A_i}$
is the quantity of the homogeneous good (agricultural) consumed by agent i, and θ
i
is a parameter that differentiates the intensity of household preferences for the quality level of the VDP.
To conform to empirical observations on the economic environment of developing economies, we first assume that all households working in the informal (either modern or agrarian) sector have the same preferences, with taste parameter
![]() ${\theta _I} = 1,\;\;$
and always decide to consume the low-quality, informally produced VDP (Q
I
). The budget constraint of these households is
${\theta _I} = 1,\;\;$
and always decide to consume the low-quality, informally produced VDP (Q
I
). The budget constraint of these households is
where
![]() ${A_I}$
is the consumption of the homogeneous good and
${A_I}$
is the consumption of the homogeneous good and
![]() $w{Q_I}$
is the price of the low-quality variety offered by informal firms. Given the above preferences, the utility-maximising demand for the homogeneous good AIN
is
$w{Q_I}$
is the price of the low-quality variety offered by informal firms. Given the above preferences, the utility-maximising demand for the homogeneous good AIN
is
Figure 2 displays the choices of a household receiving the informal wage. The two quality levels of the VDP are depicted on the horizontal axis, and the quantity of the homogeneous good (as well as household income given that P A = 1) is depicted on the vertical axis. The household’s income determines the budget constraint, which, since only two quality levels of the VDP are available, comprises just points 1 and 2.

Figure 2. Consumption behaviour of formal-sector and informal-sector households.
Low-income households select between these points, the one giving them the highest utility, which in Figure 2 is point 1 – the one associated with consumption of the informally produced, low-quality variety of the VDP.
For households earning the minimum wage, we assume that there are differences in their intensity of preferences over the quality level, implying the willingness to pay for the high-quality QF. For this income group, we assume that the taste parameter is distributed according to a continuous uniform distribution in the interval
![]() $\left[ {1,\;\varepsilon \;} \right]$
and its cumulative density function is given by
$\left[ {1,\;\varepsilon \;} \right]$
and its cumulative density function is given by
 $$D( \theta ) = \cases{ { 0 \quad\quad\quad {\hskip-3pt {\rm if} \quad\hskip18pt\theta \lt 1}} \cr {{{\varepsilon - \theta } \over {\varepsilon - 1}}}\quad\quad {{\rm if} \quad 1 \le \theta \le \varepsilon } \cr 1 \quad\quad\hskip7pt {{\rm if} \quad\hskip18pt \theta \gt \varepsilon}}$$
$$D( \theta ) = \cases{ { 0 \quad\quad\quad {\hskip-3pt {\rm if} \quad\hskip18pt\theta \lt 1}} \cr {{{\varepsilon - \theta } \over {\varepsilon - 1}}}\quad\quad {{\rm if} \quad 1 \le \theta \le \varepsilon } \cr 1 \quad\quad\hskip7pt {{\rm if} \quad\hskip18pt \theta \gt \varepsilon}}$$
For simplicity and without much loss of generality, we assume that changes in households’ employment status will be associated with changes in their preference structure; that is, households switching from informal to formal employment will acquire the preference traits (through peer pressure or social osmosis) of formal-sector households.
In Figure 2, we depict the formal-sector households with income equal to the minimum wage; their budget constraint comprises points 3 and 4. Among these households, the one with the highest value of
![]() $\theta \left( { = \varepsilon } \right)$
has a map of ‘steep’ indifference curves (one of which is denoted by
$\theta \left( { = \varepsilon } \right)$
has a map of ‘steep’ indifference curves (one of which is denoted by
![]() $\theta = \varepsilon $
) and achieves maximum utility by consuming bundle 4. As a result, the utility-maximising demand for the homogeneous good is
$\theta = \varepsilon $
) and achieves maximum utility by consuming bundle 4. As a result, the utility-maximising demand for the homogeneous good is
To ensure that this household purchases both goods, we assume that
![]() $\overline w\left( {1 - {Q_F}} \right) \gt F$
, which can be the case only if
$\overline w\left( {1 - {Q_F}} \right) \gt F$
, which can be the case only if
![]() ${Q_F} \lt 1$
. In contrast, the household with the lowest value of θ is represented by indifference curve θ=1 and chooses to consume bundle 3, that is, the informally produced good. The demand for good A by this household is
${Q_F} \lt 1$
. In contrast, the household with the lowest value of θ is represented by indifference curve θ=1 and chooses to consume bundle 3, that is, the informally produced good. The demand for good A by this household is
Equations (11) and (12) imply that for a formal-sector household with θ = θ i, the indirect utility function takes the form:
Let θ* denote the value of θ for which a household is indifferent between consuming one unit of quality
![]() ${Q_F}$
at price
${Q_F}$
at price
![]() $P\left( {{Q_F}} \right)$
and one unit of quality
$P\left( {{Q_F}} \right)$
and one unit of quality
![]() ${Q_I}$
at price
${Q_I}$
at price
![]() $P\left( {{Q_I}} \right)$
. For this household, it must hold that
$P\left( {{Q_I}} \right)$
. For this household, it must hold that
![]() $V_F^H = V_F^L$
, which implies
$V_F^H = V_F^L$
, which implies
Solving equation (12) for θ*, we find
As expected, equation (16) implies that
![]() ${{d{\theta ^*}} \over {dw}} \lt 0$
since a rise in the informal wage would increase the cost of the (low-quality) informal variety and induce more households to purchase the (high-quality) formal variety.
${{d{\theta ^*}} \over {dw}} \lt 0$
since a rise in the informal wage would increase the cost of the (low-quality) informal variety and induce more households to purchase the (high-quality) formal variety.
A formal-sector household with θ = θ * is depicted in Figure 2 as possessing the indifference curve passing from points 3 and 4.
Using the specification of the uniform distribution adopted above, we find that the number of formal-sector households that consume the high-quality variety (i.e. those with θ ≥ θ*) is equal to
![]() $\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right){L_F}$
, where LF is employment in the formal sector.
$\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right){L_F}$
, where LF is employment in the formal sector.
We assume that landowners earn significantly more than minimum-wage earners so that they always choose to consume the high-quality variety of the VDP, produced in the formal sector, implying that their consumption of homogeneous good, AT , is
where
![]() ${{\left( {1 - \alpha } \right)BL_A^\alpha } \over T}$
is the profits accruing to each of the T landowners.
${{\left( {1 - \alpha } \right)BL_A^\alpha } \over T}$
is the profits accruing to each of the T landowners.
Government sector
In addition to setting (and enforcing) the minimum wage, the government is assumed to employ workers to produce basic public services (e.g. law and order, national defence), paying these workers the minimum wage. The number of these workers is denoted by
![]() ${L_G}$
. We assume that these workers have the same preferences as formal-sector workers who also receive the minimum wage, that is, (
${L_G}$
. We assume that these workers have the same preferences as formal-sector workers who also receive the minimum wage, that is, (
![]() ${U_i} = {\theta _i}lnQ$
+
${U_i} = {\theta _i}lnQ$
+
![]() $ln{A_i}$
), with the distribution of the taste parameter
$ln{A_i}$
), with the distribution of the taste parameter
![]() $\theta $
being also given by equation (10). This implies that the number of government-employed households consuming the high-quality variety (i.e. those with θ ≥ θ*) equals to
$\theta $
being also given by equation (10). This implies that the number of government-employed households consuming the high-quality variety (i.e. those with θ ≥ θ*) equals to
![]() $\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right){L_G}$
.
$\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right){L_G}$
.
Analysis
To examine the effects of reductions in government employment, we assume that workers are mobile across sectors, and thus, should they fail to find employment either in the government sector or in the formal (modern) sector at the minimum wage, they offer their services in the informal (modern plus agrarian) sectors at the market-clearing wage,
![]() $w$
.
$w$
.
The demand for labour by formal-sector firms arises from the demand for high-quality varieties registered by two groups of households. The first group belongs to the formal-sector and government-sector households that choose to purchase the high-quality variety of the VDP; the size of this group is equal to
![]() $\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right)({L_F} + {L_G})$
. The second group consists of all landowning households (T). Thus, the demand for labour by formal-sector firms is equal to
$\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right)({L_F} + {L_G})$
. The second group consists of all landowning households (T). Thus, the demand for labour by formal-sector firms is equal to
![]() $\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right)({L_F} + {L_G}){Q_F} + T{Q_F}$
. Adding government employment to this, we get the (aggregate) demand for formal employment (
$\left( {{{\varepsilon - {\theta ^*}} \over {\varepsilon - 1}}} \right)({L_F} + {L_G}){Q_F} + T{Q_F}$
. Adding government employment to this, we get the (aggregate) demand for formal employment (
![]() $L_F^D)$
, that is,
$L_F^D)$
, that is,
Since
![]() ${{d{\theta ^*}} \over {dw}} \lt 0$
(i.e. equation (16)), we conclude that the demand for formal labour is an increasing function of the informal-sector wage rate.
${{d{\theta ^*}} \over {dw}} \lt 0$
(i.e. equation (16)), we conclude that the demand for formal labour is an increasing function of the informal-sector wage rate.
The demand for labour by informal firms in the modern sector arises from the consumption of the low-quality variety of the VDP by households (working) in both the formal and informal sectors. The number of formal-sector plus government-sector households consuming the low-quality variety is equal to
![]() $\left( {{{{\theta ^*} - 1} \over {\varepsilon - 1}}} \right)({L_F} + {L_G})$
. The number of informal and agrarian households is equal to
$\left( {{{{\theta ^*} - 1} \over {\varepsilon - 1}}} \right)({L_F} + {L_G})$
. The number of informal and agrarian households is equal to
![]() $L - ({L_F} + {L_G})$
, where L is the total number of workers/households. Thus, the demand for informal labour by low-quality producers of the VDP is equal to
$L - ({L_F} + {L_G})$
, where L is the total number of workers/households. Thus, the demand for informal labour by low-quality producers of the VDP is equal to
![]() $\left( {{{{\theta ^*} - 1} \over {\varepsilon - 1}}} \right)({L_F} + {L_G}){Q_I} + \left( {L - ({L_F} + {L_G}} \right)){Q_I}$
. Adding to this the demand for labour by the agrarian sector (see equation (4)), we get that the aggregate demand for informal labour is
$\left( {{{{\theta ^*} - 1} \over {\varepsilon - 1}}} \right)({L_F} + {L_G}){Q_I} + \left( {L - ({L_F} + {L_G}} \right)){Q_I}$
. Adding to this the demand for labour by the agrarian sector (see equation (4)), we get that the aggregate demand for informal labour is
We note that the aggregate demand for informal labour is decreasing in the informal wage rate, w, not only because the demand for labour in the agrarian sector is a negative function of the wage rate but also because an increase in w reduces the proportion of formal-sector and government-sector households purchasing the low-quality variety of the VDP.
Under the assumption of inter-sectoral labour mobility, the wage rate in the agrarian and informal sectors will be determined by the requirement that the number of labour units demanded in the informal and agrarian sectors equals the relevant labour supply. Since the latter is equal to the workers not employed in the formal and government sectors (
![]() $\;{L_I} = L - ({L_F} + {L_G}))$
, and assuming that workers prefer to find employment either in the formal or government sector (so that
$\;{L_I} = L - ({L_F} + {L_G}))$
, and assuming that workers prefer to find employment either in the formal or government sector (so that
![]() $L_F^D = {L_F}\;$
), we can state the labour market-clearing condition for workers in the informal and agrarian sectors as
$L_F^D = {L_F}\;$
), we can state the labour market-clearing condition for workers in the informal and agrarian sectors as
Equation (19), along with equations (16) and (17), can be used to solve for the market-clearing wage rate w,
![]() ${\theta ^*}$
, and
${\theta ^*}$
, and
![]() ${L_F}$
. Employment in the agrarian sector can then be determined by equation (4), which further allows to determine informal employment in the modern sector as the difference between total informal employment (=
${L_F}$
. Employment in the agrarian sector can then be determined by equation (4), which further allows to determine informal employment in the modern sector as the difference between total informal employment (=
![]() $L - ({L_F} + {L_G}))$
and employment in the agrarian sector.
$L - ({L_F} + {L_G}))$
and employment in the agrarian sector.
We now provide a diagrammatic representation of the equilibrium allocation of employment across sectors.Footnote
16
In Figure 3, the size of the horizontal axis
![]() ${O_I}{O_F}$
is equal to the total labour supply,
${O_I}{O_F}$
is equal to the total labour supply,
![]() $L$
, which is divided between (total) formal employment (=
$L$
, which is divided between (total) formal employment (=
![]() ${L_F} + {L_G})\;$
and (total) informal employment (
${L_F} + {L_G})\;$
and (total) informal employment (
![]() ${L_I}$
=
${L_I}$
=
![]() $L - ({L_F} + {L_G})).$
Informal employment is measured rightwards from the origin A, whereas formal employment is measured leftwards from the origin B
$L - ({L_F} + {L_G})).$
Informal employment is measured rightwards from the origin A, whereas formal employment is measured leftwards from the origin B
![]() $.$
The demand curve for informal labour, drawn with respect to the origin A, is depicted as the downward-sloping curve
$.$
The demand curve for informal labour, drawn with respect to the origin A, is depicted as the downward-sloping curve
![]() $L_I^D$
(equation (15)), whereas the demand curve for formal labour is drawn with respect to the origin
$L_I^D$
(equation (15)), whereas the demand curve for formal labour is drawn with respect to the origin
![]() $B$
and is depicted as the upward-sloping curve
$B$
and is depicted as the upward-sloping curve
![]() $\;L_F^D$
(equation (17)). The latter curve is drawn assuming that the (exogenous) number of government employees is measured by the line segment βΓ.Footnote
17
$\;L_F^D$
(equation (17)). The latter curve is drawn assuming that the (exogenous) number of government employees is measured by the line segment βΓ.Footnote
17

Figure 3. Effects of reductions in government employment on labour allocation across sectors.
The initial, full-employment, equilibrium allocation of labour across sectors is determined at the intersection of the
![]() $L_I^D$
and
$L_I^D$
and
![]() $L_F^D$
curves at point α, with total informal employment being equal to Α
$L_F^D$
curves at point α, with total informal employment being equal to Α
![]() $I\;$
and private formal-sector employment being equal to IΓ. The informal wage rate is equal to
$I\;$
and private formal-sector employment being equal to IΓ. The informal wage rate is equal to
![]() ${w_0}$
.
${w_0}$
.
Consider now a reduction in government employment to
![]() ${B}\Delta $
. As a result, the
${B}\Delta $
. As a result, the
![]() $L_F^D$
curve shifts to the right (
$L_F^D$
curve shifts to the right (
![]() $L_F^{D'})$
, and the new equilibrium informal wage rate drops to
$L_F^{D'})$
, and the new equilibrium informal wage rate drops to
![]() ${w_1}$
- as determined by point b, whereas there is an expansion of informal employment by
${w_1}$
- as determined by point b, whereas there is an expansion of informal employment by
![]() $IH$
units, to ΑΗ
$IH$
units, to ΑΗ
![]() $.$
Note that informal employment (modern plus agrarian) expands by more than the reduction in government employment. This happens because private employment in the formal-sector contracts is also due to the switch in demand towards the low-quality variety of the VDP produced by informal producers as a result of the drop in the informal wage rate. Thus, the informal sector’s size (both employment and output) increases not only in relationship to the total size of the formal sector (i.e. the sum of the formal private sector plus the government sector) but also in relationship to the formal private sector.
$.$
Note that informal employment (modern plus agrarian) expands by more than the reduction in government employment. This happens because private employment in the formal-sector contracts is also due to the switch in demand towards the low-quality variety of the VDP produced by informal producers as a result of the drop in the informal wage rate. Thus, the informal sector’s size (both employment and output) increases not only in relationship to the total size of the formal sector (i.e. the sum of the formal private sector plus the government sector) but also in relationship to the formal private sector.
Our framework can also be used to analyse the effects of a reduction in the public-sector wage bill without public-sector layoffs – that is, a reduction in public-sector wages. This reduction in the income of public-sector employees would induce some to switch from consuming the high-quality varieties (produced by formal firms) to the low-quality varieties offered by informal firms, thus inducing a reallocation of economic activity in the private sector from formal to informal producers.
Conclusion
Using information from all IMF conditionality programmes from 1990 to 2018, we find that public-sector dismissal programmes exert a positive and statistically significant effect on the share and absolute size of the shadow economy. We interpret this finding through the lens of a model in which worker incomes and the allocation of product demand across the formal and informal sectors are interdependent. Our finding implies that programmes aiming at public-sector employment retrenchment may be incompatible with the goal of shrinking the informal economy. This effect is more significant in countries with low institutional quality and government effectiveness.
Given that reductions in public employment are widely used as a policy instrument for meeting a country’s stabilisation and growth objectives, our analysis bears important conclusions for policy analysis. If there is a permanent structural shift towards the shadow economy, where economic activity goes untaxed, there might be adverse long-run effects on the revenue-raising ability of the government. This might undermine any initial gains to the government budget by cutting public employment. Similarly, as informal-sector firms are less technologically innovative than formal-sector ones, the shift towards the informal sector may hurt the economy’s growth prospects.
In this setting, when designing policy programmes, care should be taken to ensure that complementary policies are enacted to prevent the growth of the shadow economy, thereby avoiding the inimical effects of the increase of the informal sector. Policies aiming at improving the institutional environment of the economy, besides their direct effects, might be equally important in improving the effectiveness of other programmes. A policy approach that first seeks to strengthen the institutional framework and improve government efficiency could mitigate the adverse effects of several policies.
Beyond this, if one wishes to minimise the adverse effects of public-sector employment reductions on informality, care should be taken that formal firms receive targeted support to attract the influx of workers from the contracting public sector. Similarly, incentives for innovation, tax breaks, and income support for firms that turn to formalisation may promote the formal sector’s development and improve the economy’s growth prospects.
Overall, while public-sector employment reductions are often seen as necessary for fiscal consolidation, our study highlights the potential unintended consequences on the shadow economy. Policymakers must carefully weigh these effects and consider comprehensive strategies that address immediate fiscal needs and long-term economic health.
Acknowledgements
We thank Alfa Farah, Alexander Kemnitz, Christian Lessmann, Martin Paldam, Marcel Thum, Sofia Tsarsitalidou, and seminar participants at the TU Dresden, for valuable comments and suggestions.