Introduction
Data from the NASA/DLR (German Aerospace Research Center) Gravity Recovery and Climate Experiment (GRACE) are providing new tools for assessing mass changes of Earth’s terrestrial ice. GRACE measurements resolve the time-variable component of the Earth’s gravity field resulting from variations in the mass distribution of the atmosphere, oceans, terrestrial water and the Earth’s mantle. Using a series of background models to remove the gravity signals due to glacial isostatic adjustments (GIA), Earth/ocean tides and hydrospheric/atmospheric variations, the glacier component of change is obtained. This gravimetric measure of glacier mass change has advantages over other remote methods that rely on estimated or modeled density distributions to convert elevation to mass changes. The broad coverage of GRACE observations yields estimates of regional glacier contributions to rising sea level that are particularly valuable in regions where in situ glacier measurements are sparse.
GRACE studies of the cryosphere have focused primarily on the Greenland (e.g. Reference Velicogna and WahrVelicogna and Wahr, 2005; Reference LuthckeLuthcke and others, 2006b) and Antarctic (e.g. Reference Velicogna and WahrVelicogna and Wahr, 2006) ice sheets, which are large enough to be resolved by the relatively coarse resolution of early GRACE solution techniques. As GRACE processing techniques have evolved, the temporal and spatial resolution, as well as the fidelity of solutions to data from independent measurements, has improved. A recently developed processing technique preserves the gravity information contained within the GRACE inter-satellite range-rate measurements (Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others, 2006a) and parameterizes local mass variations as mass concentrations (mascons) (Reference RowlandsRowlands and others, 2005). The mascon approach produced maps of mass variability for six drainage basins of the Greenland ice sheet at 10 day temporal resolution that closely matched known seasonal and spatial patterns in mass loss determined from in situ and surface altimetry measurements (Reference LuthckeLuthcke and others, 2006b).
There is considerable interest in applying GRACE to mountain glaciers because these systems are making large contributions to rising sea level (Reference MeierMeier and others, 2007) and will likely play a large role in the budget of cryospheric contributions to sea-level change in the coming century (Reference Meehl and SolomonMeehl and others, 2007). Two early studies examined a subset of global spherical harmonic solutions for regions surrounding the Gulf of Alaska. Estimated mass changes were −112 ± 20 Gt a−1 between 2002 and 2004 (Reference Tamisiea, Leuliette, Davis and MitrovicaTamisiea and others, 2005), and −101 ± 22 Gt a−1 for 2002–05 (Reference Chen, Tapley and WilsonChen and others, 2006). Another study used similar techniques to assess the mass changes of mountain glaciers of the Patagonia icefields of South America using GRACE (Reference Chen, Wilson, Tapley, Blankenship and IvinsChen and others, 2007).
In a companion study, we obtained high-resolution (2 arc-degrees and 10 day sampling) GRACE mascon solutions for Gulf of Alaska glaciers, yielding a regional mass balance of −84.0± 5.0 Gt a−1 for the period April 2003–07 (Luthcke and others, 2008). These solutions were the first to make explicit corrections for the viscous component of post-Little Ice Age GIA occurring in this region (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005), and the first to incorporate atmospheric, tidal, terrestrial water and other mass-change datasets into the forward-modeling procedure. These important processing steps reduce errors due to non-glacier sources of mass change. The mass trends of Luthcke and others (2008) agree qualitatively with ground measurements and aircraft altimetry data (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002), but a rigorous comparison between GRACE and other independent datasets has not been carried out.
In this study we present aircraft laser altimetry data collected during 2000–05 and compare these with repeat flight paths acquired in 2007, in the St Elias Mountains of Alaska, USA, and Yukon, Canada. We use these data to estimate the regional mass balance of glaciers in the St Elias Mountains between September 2003 and August 2007, in order to validate GRACE mascon estimates against independent but concurrent measurements. A detailed budget of errors in mass-change estimates from GRACE and aircraft altimetry data is presented. We discuss future applications of this technique to other rapidly changing mountain glacier systems.
Data and Methods
Geographic setting
Measurements were obtained for glaciers of the St Elias Mountains of Alaska (Fig. 1). Our definition of the St Elias Mountains follows Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others (2002), but we do not include ice in the Fairweather Mountains because of the lack of sufficient altimetry data matching the GRACE measurement time interval in this region. Sixty percent of glacier surface area outlines were obtained from manual digitization of Landsat 7 Enhanced Thematic Mapper Plus (ETM+) imagery obtained between 1999 and 2001 (US National Snow and Ice Data Center/World Data Center for Glaciology, http://nsidc.org/glims/). The remaining ice areas were determined by overlaying glacier outlines digitized from topographic maps onto the same Landsat 7 ETM+ images from August 2000. These outlines were then edited to match ice extents on the Landsat images.

Fig. 1. Location of the St Elias Mountains, Alaska, USA, and Yukon, Canada. Glaciers in this region (shown in black) cover an area of 32900 km2. Red rectangles outline the dimensions of GRACE mascons 6, 7 and 10 from Luthcke and others (2008). Glaciers within the mascons but not part of our study area are shown in gray. White line marks the Canada/USA border.
Glacier area distributions with elevation (hypsometries) are required to extrapolate aircraft altimetry measurements across the study area. Hypsometries were determined by overlaying glacier outlines on a digital elevation model (DEM) of the St Elias Mountains, built from several data sources and representing year 2000 glacier geometries (Fig. 2). NASA’s Shuttle Radar Topography Mission (SRTM) 90 m DEM from February 2000 was used for all areas below 60.4° N. This was merged with the Energy, Mines and Resources Canada (EMRC) 90 m DEM derived from contours on the 1987 EMRC maps, and the US Geological Survey (USGS) 90 m DEM derived from contours on 1972 maps. A comparison was made between overlapping portions of the USGS (1972) and SRTM (2000) maps, to determine average rates of glacier surface-elevation changes as a function of elevation. Elevation changes were well represented by a linear least-squares fit to surface elevation, and this regression equation was applied to both the USGS and EMRC DEMs to bring their surfaces as close as possible to their 2000 geometry. This approach probably resulted in an overestimate of the elevation loss that occurred during this time period, because much of the overlap between USGS and SRTM DEMs was in the southern, low-elevation portion of the St Elias Mountains. The total area of glaciers in our study region is 32 900 km2, spanning a range of 0–5930 m a.s.l. The area-weighted mean elevation of all glaciers is 1600 m.

Fig. 2. Dates of US Geological Survey (USGS) and Energy, Mines and Resources Canada (EMRC) maps and the Shuttle Radar Topography Mission (SRTM) digital elevation models (DEMs) used to calculate the hypsometry of glaciers in the St Elias Mountains.
GRACE high-resolution mascons
Estimates of the mass variations of glaciers surrounding the Gulf of Alaska have been obtained from high-resolution GRACE mascon solutions (Luthcke and others, 2008). The exceptional spatial (2 arc-degrees, ∼49 000 km2) and temporal (10 day) resolution of our GRACE solution procedure is attained by preserving the gravity information contained within the GRACE inter-satellite range-rate measurements, and by parameterizing local mass variations as mass concentrations (mascons) (Reference RowlandsRowlands and others, 2005; Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others, 2006a). A set of 12 mascons were defined for the glacier regions, and the solution error for each mascon was 1–2 Gt a−1. Each solution provides an estimate of the time-averaged mass within the glacier system, referenced to the mass from the background models described above, over each 10 day interval. A series of background models were used to remove gravity signals due to glacial isostatic adjustments, Earth/ocean tides and hydrospheric/atmospheric variations. These models included the GLDAS (Global Land Data Assimilation System)/Noah 0.25°, 3 hour resolution data (Reference RodellRodell and others, 2004) used to remove gravity signals due to terrestrial water storage on land surfaces. Terrestrial water-storage corrections were set to zero for glacier areas, which were delineated using a 0.25° resolution binary glacier mask calculated from Digital Chart of the World glacier outlines (Reference Raup, Kieffer, Hare and KargelRaup and Kargel, 2000). We corrected our mascon solutions for the viscous component of post-Little Ice Age isostatic adjustments resulting from the collapse of the Glacier Bay Icefield (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005). The magnitude of this correction within the 12 glacier mascons was 7 Gt a−1.
After applying these and other background model corrections (described in detail by Luthcke and others, 2008), we assume that the residual gravity signals represent the glacier component of mass variations. In the present study we focus on glaciers of the St Elias Mountains located in mas-con gridcells 6, 7 and 10 (Luthcke and others, 2008). These mascons include glacier ice from other mountain ranges. To calculate the GRACE mass signal from glaciers of the St Elias Mountains alone, we multiplied the total signal in each mascon by the ratio of surface area of St Elias Mountain glaciers to the total ice area in each mascon. Such down-sampling assumes that the mass variations of glaciers within a mascon are spatially homogeneous.
Airborne laser altimetry
Center-line glacier surface elevations were measured in the St Elias Mountains using the University of Alaska Fairbanks (UAF) laser altimetry system (Reference EchelmeyerEchelmeyer and others, 1996; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002) and the NASA Airborne Topographic Mapper (ATM) (Reference KrabillKrabill and others, 2000, Reference Krabill2002). The UAF system measures glacier surface elevations with a 20 Hz nadir-pointing laser ranging system with average footprint separation of 2–3 m. The ATM is a 5 kHz conical-scanning laser ranging system that obtains elevation measurements for 1 m footprints within a 140 m swath, with average footprint separation of 2 m. Both systems collected elevation data along one or several flowlines of glacier tributaries, and changes in elevation were determined via comparison with elevations collected from an earlier laser profile. Laser shots collected at different times were considered to overlap in space if the horizontal distance between shots was ≤20 m. This distance was chosen based on an analysis of the repeatability of laser measurements described below.
Elevation measurements were obtained from 17 glaciers during August 2007 using the UAF laser altimetry system. Nine of these glaciers were first measured during August 2003 with the UAF system, and six during September 2005 with the ATM system. The remaining two glaciers (Yahtse and Tweedsmuir) were first measured with the UAF system during 2000 and 2001, respectively. We include these glaciers, even though their measurements occur outside the GRACE measurement time period, because it would have been difficult to estimate their non-steady behavior through extrapolation from the set of measured glaciers.
Glacier mass balances were calculated by extrapolating center-line measurements to the surface area of the glacier. We define the area of a glacier as its ice extent within its hydrologic basin, and no corrections were made for area changes occurring between measurement periods. For some glaciers elevation changes were measured in multiple basins at matching elevations. Therefore point measurements of elevation change were resampled in (x, y) space to a 20 m × 20 m grid to minimize spatial sampling biases across the glacier. Next, the surface area and elevation changes were averaged within 10 m elevation bins. Missing data were estimated by linear interpolation of surrounding measurements. In cases where data were missing at the terminus, the lowest available measurement was extrapolated to an elevation change of zero at the position of the terminus. Some high-elevation regions included steeply sloping areas that could not be sampled by altimetry. Elevation changes in these areas were assumed to be zero, following patterns observed in previous studies (Reference Aðalgeirsdóttir, Echelmeyer and HarrisonAðalgeirsdóttir and others, 1998; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002).
Elevation changes were multiplied by the glacier surface area distribution and summed to obtain a total volume change. The volume change multiplied by the density of ice (ρ
ice = 900 kg m−3) and divided by the number of years between measurements yields the mass balance of the glacier, B, in units of Gt a−1. This assumes that all mass changes occurred in the form of glacier ice, following Sorge’s law (Reference BaderBader, 1954). To compare glaciers of different sizes, B is divided by the total surface area to obtain the area-averaged mass balance ![]() in m a−1 water equivalent (w.e.). We assume that all mass balances represent the time-average mass-change rates occurring between September 2003 and August 2007, regardless of the timing of the actual measurement. This temporally aligns all measurements with the GRACE data.
in m a−1 water equivalent (w.e.). We assume that all mass balances represent the time-average mass-change rates occurring between September 2003 and August 2007, regardless of the timing of the actual measurement. This temporally aligns all measurements with the GRACE data.
Regional extrapolation
Altimetry measurements were acquired on a total of 17 glaciers with a combined surface area of 14 300 km2, ∼40% of all glaciers in the study region. We predicted the mass balance of the remaining glaciers based on an average of a subset of land-terminating glaciers in our measured sample (extrapolation ‘method C’ of Reference ArendtArendt and others, 2006). This simple approach was used because of the very large scatter in observed elevation-change measurements: averaging the elevation changes by elevation yielded a regional curve that was heavily biased by the non-steady behavior of surging and calving glaciers, and is not likely to represent other unmeasured glaciers in the region. Our altimetry measurements include >95% of tidewater glaciers in our study area and, to our knowledge, include all actively surging glaciers, leaving unmeasured glaciers that are primarily land-terminating. To represent changes on these unmeasured glaciers, we use an average of the mass balances from Barnard, Klutlan, Logan and Walsh glaciers, all land-terminating and not currently surging.
Error Analysis
Errors in mass balance from GRACE mascons
Errors in high-resolution GRACE mass trends were calculated by assuming the mass-balance time series had a first-order (lag one) autoregressive structure (Reference Lee and LundLee and Lund, 2004), yielding a 1 σ error estimate for each mascon (Luthcke and others, 2008). Systematic errors due to non-glacier mass variations from atmospheric changes, ocean tides, ocean pressure, hydrology and GIA were investigated through a sensitivity analysis, whereby two different forward models of mass variation were tested, and the difference in mascon solutions was used as an estimate of systematic errors and modeling deficiencies. These tests showed potential systematic errors had little impact on the recovered glacier mass signal (Luthcke and others, 2008).
For this study we include an additional error to account for subsampling of the 2 arc-degree mascon solution to estimate the proportion of mass change attributable to glaciers of the St Elias Mountains alone. This additional error term was included for mascons 6 and 10, the two cases where ice from glacier regions other than the St Elias Mountains was part of the solution domain and needed to be removed (see Fig. 1). We assumed that the standard deviation of the mean of glaciers measured by altimetry was an estimate of the spatial variability of all glacier balances within a given mascon. This standard deviation was multiplied by the area of St Elias Mountain glaciers within mascons 6 and 10, and summed to obtain the total subsampling error. This was added to the 1 σ GRACE error described above, to yield the total GRACE error.
Errors in mass balance determined from laser altimetry
In this section we revise and expand on several components of our laser altimetry error budget developed in previous studies (Reference EchelmeyerEchelmeyer and others, 1996; Reference Aðalgeirsdóttir, Echelmeyer and HarrisonAðalgeirsdóttir and others, 1998; Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002, Reference Arendt2006). Figure 3 summarizes random errors associated with elevation measurements and interpolation of those elevations to individual glaciers. Additional errors associated with extrapolation between glaciers, and with interannual and seasonal mass-balance variations, are described below.

Fig. 3. Plan view of center-line glacier surface altimetry measurements summarizing errors in estimating elevation changes. Elevation measurements at earlier and later times (orange: t = 1 and blue: t = 2) are considered to overlap (cross over) if the distance between them was <20 m. Each elevation measurement has a vertical positioning error, δz
pos, of 0.15 m. Errors due to slope effects, α, for points having horizontal spacing, d, are δz
slp. Elevation changes (Δz) are calculated for all M crossovers and averaged to represent the change ![]() within one of the N elevation bands. The standard deviation of all M elevation changes represents the along-flow error δΔz
af. The error in assuming the center-line measurements represent the entire area in the across-flow direction, δΔz
xf, is estimated from glacier-wide geodetic measurements from an independent study (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007).
within one of the N elevation bands. The standard deviation of all M elevation changes represents the along-flow error δΔz
af. The error in assuming the center-line measurements represent the entire area in the across-flow direction, δΔz
xf, is estimated from glacier-wide geodetic measurements from an independent study (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007).
Positioning errors
Errors in the precise positioning of an individual laser shot (δz pos) result from instrument ranging uncertainty, global positioning system (GPS) and inertial navigation system errors. Repeat measurement analysis over unchanging surfaces showed the NASA ATM system is capable of measuring surface elevations to ±0.10 m or better (Reference Krabill, Thomas, Martin, Swift and FrederickKrabill and others, 1995, Reference Krabill1999). Similar tests yielded errors of ±0.08 to 0.12 m for the UAF altimetry system. Aircraft GPS positioning errors increase with baseline distance, and are difficult to quantify. Based on these studies we assumed a value of δz pos = 0.12 m.
Repeatability errors
Data were collected on two consecutive days along the same flight path on Barnard Glacier to determine the appropriate size for a search radius in which individual shots were considered to overlap in space, and to assess the overall repeatability of the UAF altimetry measurements. We assume that for any pair of laser shots taken at different times, differences in elevation result from: (1) positioning errors (δz pos); (2) the effects of surface slope on shots with some horizontal separation (δz slp); and (3) the time evolution of the surface elevation due to ice flow and surface mass balance. Note that (1) and (2) can occur on a static and sloped surface, while (3) is the signal of change we wish to extract. We calculated δz slp = d tan α, where d is the distance between laser shots, and a is the surface slope angle. The repeatability error, δz repeat, is the quadrature sum of (1) and (2).
We calculated δz repeat for a range of r and α values and compared these with statistics describing the scatter in measured elevation changes on Barnard Glacier for different search radii. We used the interquartile range as our statistic to describe the spread in the elevation-change data, due to the non-Gaussian distribution of elevation changes. Through an iterative process we determined the threshold radius, r thr, above which the interquartile range was greater than δz repeat. Above r thr the scatter in the elevation changes exceeded the error due to positioning and slope effects, implying a detection of signal. We calculated r thr = 12 m for α = 3° and r thr = 27 m for α = 2°. We chose a value of r thr = 20 m as our search radius in order to strike a balance between the minimization of errors and the discarding of useful data. Using r thr = 20 m and a typical glacier surface slope of α = 3° yields a value of δz repeat = 1 m, which we use for the repeatability error throughout our calculations.
Across-flow Δz errors
The error in extrapolating center-line elevation-change measurements to an entire glacier surface (across-flow Δz errors, δΔz xf) has been quantified on several small glaciers in Alaska where more dense elevation-change measurements are available (Reference Sapiano, Harrison and EchelmeyerSapiano and others, 1998; Reference ArendtArendt and others, 2006; Nolan and others, 2006). These studies yield error estimates in the range 1–3 m a−1, with generally larger errors at low elevations. A larger regional study of the mass balances of glaciers in southeast Alaska was determined by differencing SRTM from USGS and British Columbia Terrain Resource Information Management (TRIM) DEMs (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). The resulting difference map provides a direct measure of the across-flow variations in surface elevation changes. Here we use this difference map from Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) to calculate the standard deviation of elevation changes within each 30 m elevation interval, and assume this represents the uncertainty in thickness changes (Reference Berthier, Arnaud, Baratoux, Vincent and RémyBerthier and others, 2004). The resulting error estimates ranged from 2 to 3 m a−1 at both low (<500 m) and high (>3000 m) elevations, likely due to the effects of low-elevation debris cover and uncertainty in high-elevation DEM surface heights, respectively. All other elevations had errors between 0.5 and 1 m a−1. For the error estimates in this study, we assign δΔz xf = 2 m for z ≤ 500 m, and δΔz af = 1 m for z > 500 m. We assume no variations in across-flow errors with time.
Seasonal and interannual errors
We assume that all elevation-change rates from altimetry measurements represent time-averaged changes occurring between 2003 and 2007, even though not all data were collected between these time periods. Differences in measurement periods may contribute to errors in our regional mass-balance calculations, due to seasonal and interannual variations in regional climatic or dynamic processes. About 1110 km2 (3%) of glaciers in our sample were measured using the NASA ATM system in 2005, and these included several maritime glacier systems presently undergoing large mass losses. We estimate the magnitude of these errors by examining data from Malaspina Glacier, the only glacier in our sample where we have UAF altimetry data (2003 and 2007) together with ATM data from 2005. In the results section below we report only the 2003–07 Malaspina data because they match the GRACE measurement window, but comparisons of 2003–05 and 2005–07 Malaspina Glacier elevations are used here to examine seasonal variability over 2 year time periods.
The area-averaged mass balance of Malaspina Glacier was −1.7 m a−1 for 2003–05, and −0.53 m a−1 for 2005–07. Using 2005–07 data alone results in a 0.6 m a−1 underestimation of our reported 2003–07 value for Malaspina (−1.10 m a−1 ). However, the patterns of elevation change as a function of elevation on this glacier are complex and reveal displacements of mass associated with surge events (Reference Muskett, Lingle, Tangborn and RabusMuskett and others, 2003; Reference Sauber, Molnia, Carabajal, Luthcke and MuskettSauber and others, 2005). Because our spatial sampling of this large and complex glacier is relatively sparse, bias estimates derived from Malaspina Glacier alone are probably not applicable to other glaciers measured during 2005. Instead, we use these results as an estimate of the potential range in mass-balance estimates possible when altimetry measurements are obtained over short time periods. We assume 0.6 m a−1 is the random error associated with seasonal and interannual climatic and dynamic variations on timescales relevant to this study. We apply this error to our area-averaged mass-balance estimates for all glaciers measured with the 2005 NASA ATM system, as well as Yahtse and Tweedsmuir Glaciers measured in 2000 and 2001, respectively. We note that none of the 2005–07 glaciers was used in the extrapolation to unmeasured glaciers, and so these seasonal and interannual errors affect only a small number of glaciers.
Density errors
Temporal variations in near-surface density result from variations in snow accumulation rate, ice velocity, temperature and moisture transport in firn, and other factors. These density variations invalidate the assumption of Sorge’s law that proscribes a time-invariant vertical profile in near-surface density. In addition, glaciers that are losing mass, such as the majority of those in our study, tend to lose old firn layers as the accumulation area becomes smaller via increases in equilibrium-line elevation. We therefore expect that our chosen density value of ρ ice = 900 kg m−3 is too high, but data or model output with which to determine a more appropriate value are lacking. Several models have been developed to estimate density variations for the dry snow zone of the ice sheets (Reference Arthern and WinghamArthern and Wingham, 1998; Reference Zwally and LiZwally and Li, 2002), but such models do not apply to Alaska glaciers where higher temperatures, melting and precipitation rates drive a more rapid densification of snow to firn and glacier ice than occurs on the ice sheets. The few available measurements or estimates for Alaska glaciers suggest a value of ρ ice = 830 kg m−3 at a site on Upper Seward Glacier (Reference SharpSharp, 1951), and a value of ρ ice = 850 ± 50 kg m−3 based on an analysis of snow and ice facies distribution on two Alaska glaciers (Reference Sapiano, Harrison and EchelmeyerSapiano and others, 1998). Both of these values are at the low end of typical glacier ice densities listed by Reference PatersonPaterson (1994).
Our strategy here is to use ρ ice = 900 kg m−3 so we can compare our results with previous altimetry estimates that assumed that density value. Although we expect density is a potentially important source of error, with no knowledge of an appropriate mean value or its variability in time or space we are unable to include it as part of our formal random-error analysis. Instead we calculate our regional balances using the minimum and maximum density values (830 and 917 kg m−3) listed by Reference PatersonPaterson (1994), yielding an error of +1.6/−0.4 Gt a−1 . These errors are not included in our reported values, but give some idea of the range in mass-balance estimates that can be expected due to density uncertainty.
Regional extrapolation errors
The errors discussed above are associated with calculations on an individual glacier. There is also uncertainty in extrapolating measured glacier changes to unmeasured glaciers. We assume that the error in ![]() of all the unmeasured glaciers is represented by the standard deviation of
of all the unmeasured glaciers is represented by the standard deviation of ![]() of glaciers measured by altimetry (0.2 m a−1), although the error may be larger, depending on the number of unmeasured glaciers exhibiting non-steady dynamic variations. Uncertainty in the outlines of unmeasured glaciers will also contribute to error in regional mass-balance estimates. These errors result from human error and the incorrect identification of surface cover type in the Landsat 7 ETM+ imagery. Correct identification of nunataks and snow cover can be especially difficult at high elevations. A case study on the Bering Glacier system showed that outlines with and without nunataks varied by ∼10% (Reference BeedleBeedle and others, 2008). Another study found that outlines of glaciers in the Chugach Mountains, Alaska, covered 10% less area than those determined from an older, less accurate map (Reference ArendtArendt and others, 2006). Although these investigations address different components of area-outlining error, they suggest that 10% is a reasonable error in the estimation of unmeasured glacier ice area in the St Elias Mountains, and this is the value we use here.
of glaciers measured by altimetry (0.2 m a−1), although the error may be larger, depending on the number of unmeasured glaciers exhibiting non-steady dynamic variations. Uncertainty in the outlines of unmeasured glaciers will also contribute to error in regional mass-balance estimates. These errors result from human error and the incorrect identification of surface cover type in the Landsat 7 ETM+ imagery. Correct identification of nunataks and snow cover can be especially difficult at high elevations. A case study on the Bering Glacier system showed that outlines with and without nunataks varied by ∼10% (Reference BeedleBeedle and others, 2008). Another study found that outlines of glaciers in the Chugach Mountains, Alaska, covered 10% less area than those determined from an older, less accurate map (Reference ArendtArendt and others, 2006). Although these investigations address different components of area-outlining error, they suggest that 10% is a reasonable error in the estimation of unmeasured glacier ice area in the St Elias Mountains, and this is the value we use here.
Summary of error budget
The total error in altimetry-derived mass balances is the quadrature sum of the positioning error, the repeatability error and the across-/along-flow elevation-change errors. In most cases the across-flow elevation-change errors dominated the error budget for individual glaciers. Seasonal and interannual errors were applied to the subset of glaciers first measured in years other than 2003. We find the error in regional mass balances of unmeasured glaciers was dominated by uncertainty in the area outlines, in agreement with previous studies (Reference ArendtArendt and others, 2006). We do not formally account for density errors because of the limited information we have to assign appropriate error values.
Results and Discussion
GRACE mascon mass-balance estimates
The trend in GRACE mascon estimates of glaciers in the St Elias Mountains between September 2003 and August 2007 was −20.6 ± 3.0 Gt a−1 (Fig. 4). Summer balances were greater in magnitude than winter balances within each balance year, with the largest negative summer balance occurring during 2004 (Table 1). This coincided with record high air temperatures throughout Alaska, and record negative mass balances at Gulkana Glacier in central Alaska (Reference Truffer, Harrison and MarchTruffer and others, 2005). Variability in B was driven by variations in the summer balance, B s, as both B s and B became progressively less negative between 2003 and 2007.

Fig. 4. Cumulative mass-balance time series (September 2003 to August 2007) for all glaciers in the St Elias Mountains from GRACE: 10 day estimates (blue dots with error bars); Gaussian 1 day filter with 10 day window applied to 10 day estimates (green curve); and trend (red line) recovered from simultaneous estimation of bias, trend, annual and semi-annual sinusoids. Error bars indicate 1 σ uncertainties.
Table 1. Regional winter (B w), and summer (B s), balances in the St Elias Mountains between 2003 and 2007, determined as the difference between maximum/minimum cumulative mass balances in the GRACE mascon time series (Fig. 4). Annual balance, B, is the sum of winter and summer values in a balance year. Balance years begin during the fall of the previous calendar year. Balance amplitudes are the average of summer and winter balance magnitudes (absolute values), following Reference MeierMeier (1984)

Altimetry measurements
Rates of elevation change in the St Elias Mountains between 2000–05 and 2007 illustrate a wide variety of dynamic conditions resulting from climatic variations, surge behavior and tidewater/lacustrine glacier dynamics (Fig. 5; Table 2). Bering Glacier is thinning in the elevation range 1000–2000 m and thickening in the range 500–1000 m. This drawdown of mass from an upper reservoir area to a lower receiving area is indicative of active surge behavior on this glacier which last surged during 1993–95 (Reference Lingle, Post, Herzfeld, Molnia, Krimmel and RoushLingle and others, 1993). Tweedsmuir Glacier has similar patterns of elevation change. The surge of this glacier initiated sometime during the winter of 2006/07, and at the time of our August 2007 altimetry flights the surge was fully developed. Tana Glacier, thickening in its ablation zone, shares a divide with Bering Glacier and may be influenced by the Bering Glacier surge cycles. Malaspina Glacier has complex flow dynamics associated with surge pulses that alternate between central and eastern portions of the piedmont lobe (Reference Muskett, Lingle, Tangborn and RabusMuskett and others, 2003; Reference Sauber, Molnia, Carabajal, Luthcke and MuskettSauber and others, 2005). Our three profiles covering the piedmont area do not capture this complexity, but areas of thickening along the eastern and upper portion of the central lobe are likely to be associated with surge dynamics.

Fig. 5. Elevation rate (m a−1) of glaciers in the St Elias Mountains (gray shading) determined from aircraft laser altimetry. Glacier names associated with the three-letter symbols, and dates of altimetry measurements, are given in Table 2.
Table 2. Summary of aircraft laser altimetry measurements in the St Elias Mountains. ‘Symbol’ is a three-letter code identifying each glacier; ‘Type’ describes whether the glacier is land-terminating (L), lake-terminating (LK) or tidewater (TW); ‘Area’ is the glacier surface area; B is the mass balance; ![]() is the area-averaged mass balance. Measurements were obtained with the University of Alaska Fairbanks (UAF) laser system, except those in 2005, which were measured using NASA’s ATM system, labeled ‘*’
is the area-averaged mass balance. Measurements were obtained with the University of Alaska Fairbanks (UAF) laser system, except those in 2005, which were measured using NASA’s ATM system, labeled ‘*’
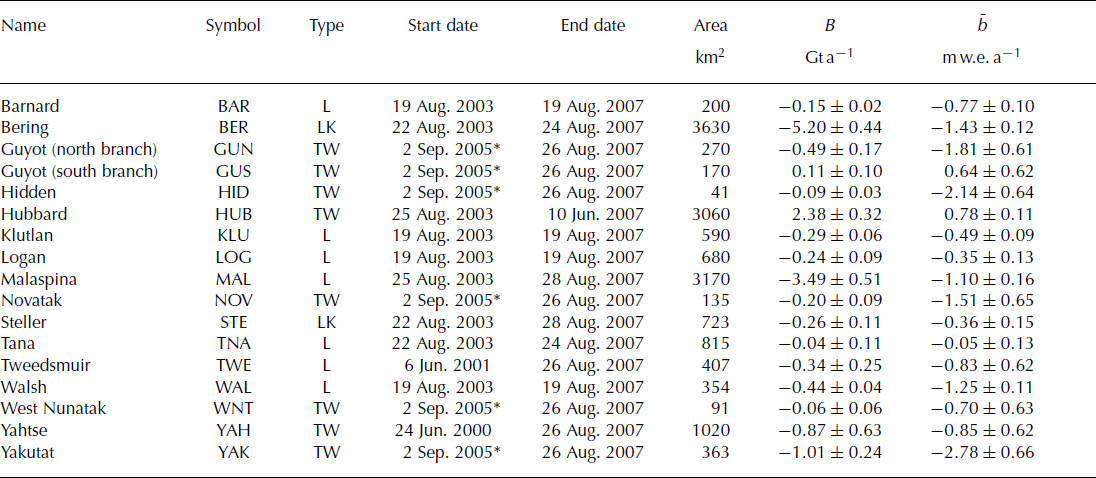
Complex tidewater glacier dynamics are affecting glaciers terminating in Icy Bay, and our measurements illustrate the capacity for these glaciers to undergo extremely rapid changes in elevation over the span of a few years. The north branch of Guyot Glacier had an area-averaged mass balance of −1.81 ± 0.61 m w.e. a−1, with an elevation rate of −54 m a−1 near the terminus, during 2005–07. To our knowledge this is the most negative elevation rate ever measured on an Alaska glacier. The surface elevation of Yahtse Glacier decreased over most of its length between 2000 and 2007, but the glacier terminus also advanced during this time. This is unusual behavior that does not follow patterns typical of the tidewater glacier cycle (Reference Meier and PostMeier and Post, 1987), wherein glaciers exhibit a phase of relatively fast thinning and retreat followed by a much longer period of slow advance. Hubbard Glacier, terminating in Yakutat Bay, continued its phase of tidewater glacier advance (Reference Motyka and TrufferMotyka and Truffer, 2007), with slow terminus advance and elevation gain over most of its length. Glaciers of the Yakutat Icefield, including Yakutat, Novatak, Hidden and West Nunatak Glaciers all had negative elevation changes, resulting in a net loss in mass ![]() of the entire icefield. This icefield lacks any accumulation area, and it will likely disappear under any plausible future climate scenario. Steller Glacier is lake-terminating and had large negative elevation rates at the terminus that are similar to those occurring on a tidewater glacier system. The remaining land-terminating glaciers include Barnard, Klutlan, Logan and Walsh Glaciers and, in general, these had negative elevation rates at the terminus and an increase to near-zero or slightly positive rates at high elevations. We note that Logan and Walsh Glaciers are surge-type glaciers that are presently in the quiescent phase of their surge cycles.
of the entire icefield. This icefield lacks any accumulation area, and it will likely disappear under any plausible future climate scenario. Steller Glacier is lake-terminating and had large negative elevation rates at the terminus that are similar to those occurring on a tidewater glacier system. The remaining land-terminating glaciers include Barnard, Klutlan, Logan and Walsh Glaciers and, in general, these had negative elevation rates at the terminus and an increase to near-zero or slightly positive rates at high elevations. We note that Logan and Walsh Glaciers are surge-type glaciers that are presently in the quiescent phase of their surge cycles.
Combining all altimetry measurements yields a mass balance of −10.7 ± 1.1 Gt a−1. Extrapolating the land-terminating glacier mass balances to all unmeasured glaciers yields an additional mass balance of −10.6 ± 3.6 Gt a−1. The total mass balance of glaciers of the St Elias Mountains as estimated from aircraft altimetry for the period September 2003 to August 2007 was −21.2 ± 3.8 Gt a−1.
Comparison of GRACE mascon and altimetry measurements
The difference between altimetry (−21.2 ± 3.8 Gt a−1) and high-resolution GRACE mascon (−20.6 ± 3.0 Gt a−1) estimates of glacier mass balance in the St Elias Mountains during 2003–07 was −0.6 ± 4.8 Gt a−1. The difference is well within estimated errors, and could be partially accounted for by uncertainty in the near-surface density. Supposing that our mass-balance and error estimates are exact, our results suggest that an ice density, ρ ice = 900 kg m−3, used in previous altimetry studies in Alaska may need to be revised downward. This finding is consistent with preliminary comparisons between GRACE and surface altimetry mass-balance estimates on the Greenland ice sheet, where ATM estimates were more negative than GRACE mascon solutions for similar time periods (Reference LuthckeLuthcke and others, 2007). Further modeling and field efforts should be carried out to investigate near-surface variations in density to increase accuracy in altimetry mass-balance estimates.
Both the GRACE mascon and altimetry mass-balance estimates are close to those determined exclusively from aircraft altimetry for earlier time periods. Regional mass balances were approximately −25± 10 Gt a−1 for glaciers of the St Elias Mountains during both the 1948–72 to 1995/96, and the 1995/96 to 2000 periods (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). These altimetry calculations were conducted over a larger area (40 700 km2) than in the present study, due to the slightly expanded definition of the St Elias region used by Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others (2002), and the fact that area outlines used for that analysis were less accurate than those used here. Scaling the mass balance during these earlier periods to the area of glaciers defined in the present study yields a value of about −20 ± 8.0 Gt a−1, a rate that is similar to our reported values for 2003–07 from GRACE and altimetry. Therefore, on a regional scale, glaciers of the St Elias Mountains appear to have been steadily losing mass at approximately the same rate during the past several decades. This is in contrast to other regions in Alaska, where mass balances have become increasingly negative during the last decade relative to the previous 50 years.
Application to other regions
The ability of GRACE mascon solutions to resolve regional glacier changes increases with the amount of ice cover within a region, and the absolute magnitude of mass change occurring in that region. About 30% of the surface area of the mascons covering the St Elias Mountains consists of ice cover. The area also has a rapid rate of glacier mass loss, creating a signal that was well resolved by our high-resolution GRACE solutions.
To what extent will the methods described in this paper provide accurate regional mass-balance estimates for other glacier regions on Earth? We assume the regional GRACE mass-balance error calculated for Alaska glaciers (±3 Gt a−1) applies to other regions, and calculate the minimum area-averaged regional balance, ![]() , required in a glacier region that exceeds this error. For the Patagonia Icefields of South America (13% ice cover) and glaciers of the Canadian Arctic (17% ice cover),
, required in a glacier region that exceeds this error. For the Patagonia Icefields of South America (13% ice cover) and glaciers of the Canadian Arctic (17% ice cover), ![]() and 0.35 m a−1, respectively. On the Patagonia Icefields,
and 0.35 m a−1, respectively. On the Patagonia Icefields, ![]() between 1995 and 2000 (Reference Rignot, Rivera and CasassaRignot and others, 2003), and if this rate has continued through 2007, mass losses in this region will well exceed GRACE errors. In the Canadian Arctic, an extrapolation of ATM measurements acquired between 1995 and 2000 yielded
between 1995 and 2000 (Reference Rignot, Rivera and CasassaRignot and others, 2003), and if this rate has continued through 2007, mass losses in this region will well exceed GRACE errors. In the Canadian Arctic, an extrapolation of ATM measurements acquired between 1995 and 2000 yielded ![]() (Reference AbdalatiAbdalati and others, 2004), a rate that would be below GRACE errors. However, changes at specific ice caps, such as Devon Ice Cap with
(Reference AbdalatiAbdalati and others, 2004), a rate that would be below GRACE errors. However, changes at specific ice caps, such as Devon Ice Cap with ![]() (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005) would well exceed GRACE errors, and recent changes in the Canadian Arctic might be larger than those that occurred prior to 2000. Changes of glaciers in Iceland, Franz Josef Land, Svalbard and the Karakoram might also be resolvable by GRACE, although we lack recent information on their regional mass-balance magnitudes. We note that the error in individual mascon trends might be lower in other regions than in Alaska, due to different error contributions from non-glacier sources of mass change.
(Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005) would well exceed GRACE errors, and recent changes in the Canadian Arctic might be larger than those that occurred prior to 2000. Changes of glaciers in Iceland, Franz Josef Land, Svalbard and the Karakoram might also be resolvable by GRACE, although we lack recent information on their regional mass-balance magnitudes. We note that the error in individual mascon trends might be lower in other regions than in Alaska, due to different error contributions from non-glacier sources of mass change.
Conclusions
Glaciers in the St Elias Mountains exhibited a complex pattern of elevation change during the period 2000–05 to 2007. Of the 17 glaciers measured during this time, three showed signs of preliminary or active surge dynamics and eight were tidewater glaciers in different stages of their tidewater glacier cycle. There were no consistent patterns in regional-scale elevation change as a function of elevation on the 17 glaciers measured with altimetry. Despite this complexity, the integrated, glacier-wide balances produced regional estimates of mass balance (−21.2 ± 3.8 Gt a−1) that agreed very well with GRACE mascon mass-balance estimates (−20.6 ± 3.0 Gt a−1). We suggest that integrating elevation changes over each individual glacier basin helps to minimize local dynamic effects and leads to a more robust estimate of regional mass balances.
Our mass-balance estimates agree closely with altimetryderived estimates for periods reaching back to ∼1950, for approximately the same glacier region. Unlike other regions in Alaska, glaciers of the St Elias Mountains do not appear to be losing mass at an increasing rate. This might be the result of complex dynamic cycles associated with tidewater/lacustrine and surge events that complicate the relationship between regional mass loss and climate warming.
The close correspondence between our altimetry estimates and a subset of high-resolution GRACE solutions for the St Elias region lends confidence to the GRACE mascon solution procedure. It suggests that GRACE errors resulting from non-glacier sources of mass variation have been minimized, allowing for the recovery of glacier mass changes at an accuracy similar to that which can be achieved with altimetry measurements. This high-resolution GRACE mascon technique should be applied to other glacier regions on Earth experiencing rapid rates of mass loss, so as to improve global estimates of mountain glacier contribution to rising sea level.
Acknowledgements
This work was supported by NASA under the GRACE Science Team, Interdisciplinary Sciences and Cryospheric Sciences Programs, and US National Science Foundation (NSF) Office of Polar Programs (OPP) grant NAG5-13760. K. Echelmeyer collected the 2000–01 UAF altimetry data. Paul Claus (pilot) and Donna, Jay, Eleanor and John Claus at Ultima Thule Lodge provided aircraft and logistical support for the 2003 and 2007 UAF field operations. C. Lingle, S. Zirnheld, I. Das and B. Ritchie assisted with UAF altimetry field-data collection and processing. S. Seibold and W. Clark of Twin Otter International Ltd supported the 2005 field operations. J. Sonntag, E. Frederick, R. Russell, S. Manizade and R. Muskett assisted with NASA ATM data collection and processing. D. Rowlands assisted with GRACE processing. Reviews from G. Cogley and J. Wahr substantially improved the manuscript.









