List of Symbols


Introduction
Stresses within and at the bed of glaciers can be calculated by solving a boundary-value problem involving the stress-equilibrium equations, compatibility equations and a specified constitutive relation. The necessary data include temperature distributions (assumed constant at the pressure-melting point in this paper), the geometry of the surface and bed, and velocity-boundary conditions. The basal geometry may be determined by radar but, because the velocity data can only be efficiently and economically collected on the surface of a glacier, all the necessary boundary conditions must be specified on only one of the boundaries (the surface) rather than both (the surface and the bed). This unbalanced distribution of boundary conditions is still mathematically sufficient to determine the englacial velocity and stress state uniquely. Unfortunately, when all the boundary conditions are specified at the surface, the boundary-value problem becomes ill-posed and unstable (Reference Courant and HilbertCourant and Hilbert, 1966, p. 227–30; Reference LliboutryLlib-outry, 1987). Small changes in the surface velocities will correspond to disproportionately large velocity and stress changes at depth, and small errors in surveyed surface velocities will translate to very large errors in the calculated velocities and stresses at depth. These errors may be large enough to mask the true velocity and stress signals.
Without a viable alternative, glaciological research (as well as other branches of geophysics such as seismology) has continued to focus on ill-posed models which calculate englacial velocities from data acquired only at the surface (e.g. Reference Frolich, Mantripp, Vaughan and DoakeFrolich and others, 1987; Reference Raymond, Jóhannesson and PfefferRaymond and others, 1987; Reference Van der Veen and WhillansVan der Veen and Whillans, 1989a). This necessitates very careful interpretations of velocities calculated at depth with special attention paid to the potential ill-posed calculation instabilities. Physical intuition may aid in the elimination of unreasonable basal velocities (e.g. high-amplitude centimeter wavelength fluctuations) but a more precise analysis of error propagation would be preferable.
While some studies have performed numerical model-sensitivity analyses (e.g. Reference Van der Veen and WhillansVan der Veen and Whillans, 1989b), very few papers have attempted theoretical studies of the effects that surface-velocity errors or velocity perturbations have on calculations of velocities and stresses at depth. Research has focused primarily on perturbations in bedrock or surface geometries and the consequent changes in flow (Reference BuddBudd, 1970; Reference Echelmeyer and KambEchelmeyer and Kamb, 1986; Reference JóhannessonJóhannesson, 1992). Reference Hantz and LliboutryHantz and Lliboutry (1981) and Reference LliboutryLliboutry (1987) discussed the ill-posed problem in terms of a von Neumann stability condition on finite-difference approximations to the stress equilibrium and other continuum equations but did not extend their analysis to the full undifferenced flow equations. Reference Balise and RaymondBalise and Raymond (1985) made significant advances by deriving exact analytical expressions for surface-velocity anomalies as a function of known basal velocity anomalies but the assumptions regarding a linear viscous (Newtonian) material and planar slab geometry limit the applicability of their results. Reference BaliseBalise (1988) discussed additional findings for non-linear flow but considered only numerical solutions.
In contrast to these earlier analyses, the theoretical developments of this study use a non-linear constitutive relation (Glen’s flow law for ice) to derive analytical relations between surface-velocity measurement errors and the consequent uncertainties in velocities and stresses at depth. The geometry is plane-parallel so that perturbations from simple extensional and compressional flow solutions will apply. Like most previous studies, a state of plane strain is also assumed. This effectively reduces the geometry of the problem to two dimensions by neglecting the influence of transverse velocity variations and, as a consequence, this analysis will apply mostly to very wide glaciers where the effects of valley side walls are minimized. The plane-strain assumption also necessitates that the surface perturbations extend across the width of the glacier or at least be large compared to the length of the study area. While many polar ice streams fit these restrictions, the glaciers must be assumed temperate to decouple the thermal processes from the otherwise very complicated thermomechanical flow. However, the careful application of the theory to non-temperate ice and smaller temperate glaciers should still provide valuable information.
Preliminary Derivations
The influence of surface-velocity errors on stresses at depth in a glacier can be quantified by considering perturbations from the boundary-value equations described by Reference LliboutryLliboutry (1987), Reference MaseMase (1970) and many others. These equations describe the state of stress within any two-dimensional (plane-strain) isothermal glacier and can be quickly modified to represent errors or perturbations from some steady-state stress distribution. For axes along the surface of a plane-parallel glacier, positive depth downwards (Fig. 1), the boundary-value equations are


and

with the boundary conditions (derived in Appendix 1)



and


Fig. 1. Cartoon representation of velocity profiles for linear and highly non-linearly viscous ice. Note two-dimensional geometry and coordinate syste, positive depth downwards. Flow is in the positive x direction.
Now, if

which implies

Similarly, the remaining boundary-value equations can be perturbed to give


and

with the boundary conditions



and

Notice that for this analysis we are only interested in the consequence of inaccuracies (e.g. measurement errors) in the specified surface velocities. The geometry of the glacier, therefore, is fixed and the slope α is left unperturbed.
These Equations (3) describe the ill-posed boundary-value problem for stress perturbations
The next section solves the perturbed boundary-value problem (Equations (3)) for stress perturbations from compressional and extensional flow solutions (used as the reference flow state). The derivations are especially complicated for non-linearly viscous flow, so a small stress perturbation assumption is used to linearize the problem. The multiple tensor components are reduced to a single variable with a stress function, not unlike the Airy function often used with Newtonian flow. The stress function trivially satisfies the stress-equilibrium equation and leads to a statement of the compatibility equation which can be Fourier transformed and solved as an ordinary differential equation. The solutions are discussed in a later section.
Perturbation Analysis
Most temperate glaciers can be roughly divided into two flow regimes, extensional above the equilibrium line and compressional below the equilibrium line. It follows that perturbations from extending and compressing flow will characterize many realistic flow patterns and should lead to relatively general conclusions about the influence of surface-velocity uncertainties. From Reference NyeNye (1957), for a plane-parallel geometry with a constant longitudinal surface-velocity gradient, the compressional and extensional stress solution is given by
and

where
At this point, the analysis will be restricted to situations with highly compressive and highly tensile flow so that

In this case, Equation (4b) reduces to

for all values of n. This simplification is necessary to solve the very complicated relationships in Equations (3). However, when the surface slope is small, as it is in many glaciers, Equation (6) is first order accurate without any assumption of very compressive or very tensile flow. Also, assumption (5) will be true in glaciers which are decoupled from the bed, so that basal sliding rates are high and basal shear stresses are low. Regions of intense compression or extension would then have greater longitudinal stresses than shear stresses. On Columbia Glacier, for example, which is largely decoupled from its bed, surface strain rates in excess of 3 × 107 s−1 have been measured for extension and compression (Reference Meier, Rasmussen, Krimmel, Olsen and FrankMeier and others, 1985). With A = 5.3 × 10−15 s−1 kPa−3 (Reference PatersonPaterson, 1981, p. 39), this corresponds to very large longitudinal surface stresses on the order of 200 kPa. Surging glaciers such as Variegated Glacier in 1984 may also satisfy this requirement.
To simplify the analysis even further, we will also assume that the stress perturbations are small, i.e.

Now, by using assumptions (5) and (7), the constitutive equations can be linearized by neglecting small terms. As derived in Appendix 2,

and

The boundary-value problem, summarized in Equations (3), can now be solved with the perturbed Glen’s flow law (Equations (3c) and (3d)) replaced by the equivalent linearized constitutive equations. Substituting expressions (8a) and (8b) into the perturbed compatibility Equation (3b) yields

By Equation (6), the compatibility equation reduces to

Now define a stress function Ψ (analogous to the Airy stress functions of Newtonian flow) such that

and

These definitions trivially satisfy the perturbed stress-equilibrium Equation (3a) and reduce the number of unknowns from two to one in the compatibility equation, i.e.

or

Fourier-transforming all variations with x to the spatial frequency domain reduces Equation (11b) to a fourth-order ordinary differential equation

where k is the spatial frequency in the χ direction and a caret indicates a Fourier-transformed function.
By substituting Φ into the boundary conditions (Equations (3e) through (3h)),



and

where ΔN(x) equals the perturbed Neumann boundary condition given on the righthand side of Equation (3h). (For this particular case

Now, by Fourier-transforming each term in Equations (13), boundary conditions for Equation (12) are


and

Solving Equation (12) with boundary conditions in Equations (14a) through (14d) gives
where


and




Using the transforms of Equations (10a) and (10b),

and

Using trigonometric identities, these reduce to

and

Note that for all z

and

By substituting these absolutely convergent power series into Equations (19) and inverse Fourier-transforming term by term, we find

and

These are the final perturbation solutions and will be discussed in detail in the next section.
Discussion and Derivation of Lyapunov Exponent
To keep truncation errors in the perturbation solutions in Equations (21a) and (21b) at a minimum, large numbers of series terms may be required; but, as the number of series terms is increased, the perturbation solutions show an increasing dependence on higher-order derivatives of the surface-boundary conditions. Specifying these higher-order derivatives requires increasing spatial resolution in the data, which implies an increasing sensitivity to high spatial frequencies. Unfortunately, the majority of measurement errors will occur at high frequencies; so greater calculation accuracy necessitates using data at short wavelengths where they are inaccurate and this causes a calculation instability.
This calculation instability is especially clear in the spatial frequency domain. From Equations (18), we see that the stress errors increase exponentially with increasing frequency, k. In fact, this is indicative of an unstable divergence from the unperturbed solution, with greater divergence in the calculations at increasing frequencies.
If we restrict our attention to longitudinal perturbations and assume for the moment that vertical velocity errors are negligible (so ΔN(x) = 0), we can assess the rate at which perturbations grow or, in other words, the rate of information loss. This is done quantitatively by using a Lyapunov exponent, λl , defined approximately by

for an appropriate norm, ||·||, such as the supnorm (see Reference ApostolApóstol, 1969). Intuitively, λl just describes the rate at which errors are growing with depth. If λl is positive, then the errors grow exponentially and the system is described as chaotic. In this context, chaos does not refer to the behavior of the glacier itself but instead refers to the very unstable divergence of calculation errors caused by the ill-posed placement of the boundary conditions at the surface of the glacier, λl measures the degree of chaos within the calculation process only.
Chaos itself is an often-misunderstood term with a number of different definitions within the literature but, intuitively, a chaotic process is any system for which long-term prediction of the system’s state is impossible because uncertainties in the initial state grow exponentially with time (see, for example, Reference Wolf and HoldenWolf, 1986; Reference GulickGulick, 1992). For steady-state glacier-velocity and stress calculations, the initial state is replaced by the surface-boundary conditions and time is replaced by depth. Then, by analogy, the stress calculations within a glacier (not the glacier itself) are chaotic if uncertainties in the boundary conditions (surface velocities) grow exponentially with increasing depth. For the purposes of this analysis, we will follow the common convention of equating chaos with a positive Lyapunov exponent.
Rigorously, the Lyapunov exponent for a function F at x is defined as

(See, for example, Reference GulickGulick, 1992.) In the case of stress calculations, F (as a function of x) is replaced by

is replaced by the equivalent

So,

Now, using Equations (19a) and (23d), the Lyapunov exponent is given by

By converting to complex exponentials, the limit, after some manipulation, reduces to

(see Appendix 3), where Re[s(n)] is the real part of s(n). In other words, the Lyapunov exponent is a linear function of frequency. At k = 0 (infinite wavelength), no information is lost but as k increases so does the Lyapunov exponent. This means information is lost at an increasing rate with frequency or, in other words, the stress calculations are increasingly chaotic with increasing frequency. For practical applications, this means high-frequency information at the bed will be irretrievable from information gathered at the surface.
If we change assumptions and let
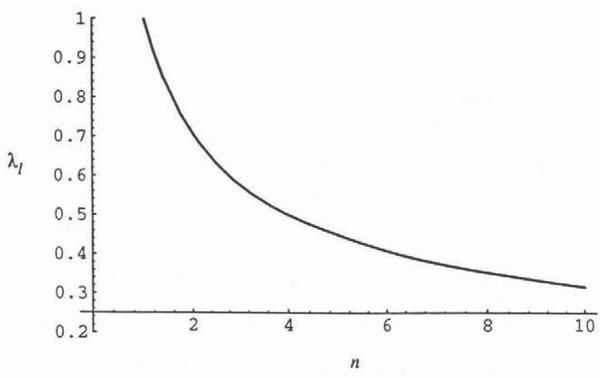
Figure 2 shows a plot of Re[s(n)] as n varies from 1 to 10. This coefficient to the Lyapunov exponent decreases rapidly from a value of 1 at η = 1 to roughly 0.6 at n = 3. The decreasing values show that errors in the stress calculations are decreased by increasing non-linearities in Glen’s flow law. Roughly speaking, at n = 3 the rate of information loss is only six-tenths the rate of loss for n = 1. Though counter-intuitive, the following examples help explain this calculation behavior.

Fig. 2. The Lyapunov exponent, λlas η varies from 1 to 10. (k is fixed at 1.)
First, consider a glacier in simple shear where η is approaching infinity, so that Glen’s flow law becomes perfectly plastic (Reference PatersonPaterson, 1981, p. 40) and no deformation takes place in the ice between the surface and the bed (the yield stress will be exceeded only at the bed). In this case, no information is lost because any velocity at the bed must be transmitted rigidly to the surface and, therefore, in the limit as n → ∞, the Lyapunov exponent must be zero. Therefore, the Lyapunov exponent must be a decreasing function of n, at least in the asymptotic limit.
As another example, consider two glaciers, one of them linear-viscous and the other one highly non-linear. For each glacier, there is a zone near the bed where deformation is greatest and above this zone the ice is comparatively rigid with far less deformation. If there is a velocity perturbation at the bed, this perturbation will be largely accommodated within the zone of high deformation. For the non-linear ice, this zone will be much smaller than for the linear ice (Fig. 1). This means that the basal perturbation’s effects fall off more rapidly with distance from the bed for the non-linear material relative to the linear material. In other words, information about the perturbation will be lost more rapidly with distance from the bed for the non-linear viscous material relative to the linear viscous material. This has been demonstrated numerically by Reference BaliseBalise (1988).
However, an observer on the surface of the glacier sees the effects of the basal traction as a velocity perturbation at the surface. This velocity perturbation at the surface can be inverted for the velocity perturbation at any depth. Comparatively little deformation is occurring in the ice above the zone of greatest deformation which is near the bed, so information about the perturbation is transmitted across this overlying “rigid” region, up to the surface, with relatively little loss of information. This “rigid” region is much larger for the non-linear viscous ice than it is for the linear viscous ice (Fig. 1). Therefore, we can invert for information about the perturbation to a greater depth in the non-linear viscous ice (by inverting across this “rigid” region). The perfectly plastic example above is just the limiting case where the rigid region occupies the entire thickness of the glacier. Of course, as Reference BaliseBalise (1988) showed, more information is lost in a nonlinear viscous material because of the enhanced deformation near the bed but we can still invert for the pertur-bation to a greater depth.
These arguments agree with the Lyapunov-exponent analysis which claims that information about the perturbation decreases at an exponential rate with depth. However, as n increases, the magnitude of error will remain the same if z also increases. In other words, for any specified error magnitude, we can invert to a greater depth with a non-linearly viscous fluid. While these analytical derivations assume highly compressive or tensile flow, the arguments in the preceding paragraphs demonstrate that the analysis is more generally valid.
Note that, if a traction is applied to the surface of the glacier instead of the bed, the preceding arguments will not be true. In that case, the non-linearly viscous ice will deform in a small region near the surface (relative to a larger region for the linear viscous ice). This means that the perturbations are more rapidly suppressed with depth by the non-linear ice relative to the linear ice. In other words, information about a traction applied at the surface will be lost more rapidly with depth for the non-linearly viscous material.
Also, the preceding arguments imply that all the very interesting deformation in a glacier is occurring in a layer close to the bed and that this layer gets smaller with increasing non-linearity. Therefore, the only reason we can invert for information in a larger region of the non-linearly viscous glacier is because there is a larger region where nothing interesting is happening. In the perfectly plastic case, we can invert all the way to the bed but all the interesting physics will be in an infinitesimally small layer which is invisible to the mathematics. Furthermore, because of the high attenuation near the bed in the nonlinear case, any measured deviations at the surface are much less likely to be caused by a physical process at the bed, and instead may be due to ice anisotropics, in homogeneities or other processes within the comparatively rigid part of the glacier. Inverting for information at the bed based upon observations at the surface may be attributing the origin of a surface perturbation to the wrong location.
Conclusions
With a flow-law exponent of n = 3, velocity and stress calculations (which start at the surface and invert for velocities at depth) lose information at only six-tenths the rate of calculations with a linear viscous constitutive law. Nevertheless, the overall behavior of these non-linear calculations is still unstable and divergent. This highly unstable calculation behavior can be illustrated hypothet-ically by assuming we own a nearly perfect surveying device and that the entire survey process can find velocities with atomic precision (± 1 Ångstrom d−1). Also, suppose that we are not very particular, and we only desire velocities at the bed (z = H) to be within ±100 m d−1. Then, for n = 3, from expression (22), 100 m d−1 ≈ 10−8 cm d−1
For small glaciers with small surveying distances, a more realistic survey accuracy is on the order of 0.1 cm d−1. So with n = 3, achieving a more reasonable 10 cm d−1 accuracy at the bed will only be possible when 10 ≈ (1/10)e0.6kH and, therefore, k − 7.7 H −1 or λ = 2π/k − 0.8H. This number varies between roughly 0.5 and 1.5 ice thicknesses as the measurement accuracies and required basal accuracies change by an order of magnitude. So, roughly speaking, with standard surveying precision, accurate calculations are theoretically possible for wavelengths greater than about one ice thickness but will be much harder or impossible for wavelengths shorter than one ice thickness. For Newtonian flow, the results are qualitively similar, even though the non-linear flow calculations are technically less divergent.
As another example, consider Variegated Glacier (Alaska) approximately 2 km from the terminus as it existed on 29 June 1984, just after the surge front had passed. Reference Raymond, Jóhannesson and PfefferRaymond and others (1987) surveyed the glacier with positioning accuracies of roughly 1 cm d−1. The errors in the velocities, therefore, are on the order of √2 cm d−1 (velocities are calculated from differences in subsequent positions of a stake). The glacier in this section is roughly 125 m thick with a surface slope of roughly 0.05 rad. The flow-law exponent, n, is assumed to be 4.2 (Reference Raymond, Jóhannesson and PfefferRaymond and others, 1987). The surface velocities center around 35 m d−1 and, using simple laminar-flow approximations (e.g. Reference PatersonPaterson, 1981, p. 87), the velocities at the bed are also expected to be on the order of 35 m d−1 (very slightly less). At a wavelength equal to the thickness, the basal-velocity calculation errors are given by
Variegated Glacier is unusual because of its surge-type behavior and especially rapid sliding velocities but, if the expected basal velocities were much slower, the per cent error for wavelengths on the order of one ice thickness would change only slightly compared to the change for shorter wavelengths. For example, if the basal velocity is expected to be on the order of 1 m d−1, then at a wavelength of one ice thickness the errors are 30%. But, at one-third the thickness, the errors are 14000% of the expected basal velocities. Obviously, this is the difference between some information and absolutely no information at all.
These results are limited by two primary assumptions: small-stress perturbations and plane-parallel geometries. Many glaciers are closely approximated by low-angle, plane-parallel geometries, so the conclusions should be first-order representative of many realistic scenarios. However, the small-perturbation assumption (for linearization of the non-linear constitutive equation) is a much more severe limitation. Deviations from compressive and extensive flow may be quite large at the surface and, in order for the perturbations to remain small compared to the datum state at all depths, the surface perturbations must be quite small. However, the general rate at which errors grow with depth (the Lyapunov exponent) is unaffected by the size of the errors. Extremely small surface errors will still grow exponentially with depth, ensuring rapid divergence from the reference velocity and stress solutions.
Acknowledgements
This work was supported by a University of Colorado Graduate School Fellowship, by U.S. National Science Foundation grants DPP-8619348 and DPP-9122916, and by a Department of Energy grant, DE-FG02-90ERG-1078. We should like to thank D. MacAyeal, C. Raymond and an anonymous reviewer for valuable comments and discussions which helped improve this manuscript.
The accuracy of references in the text and in this list is the responsibility of the authors, to whom queries should be addressed.
Appendix 1 Derivation of Boundary Conditions
To find

To keep the surface shear-free ((t x, t z) = (0, P)) Equation (A1.1) requires
The other Dirichlet boundary condition,
The remaining Neumann boundary conditions,

From Equation (A1.2),

and, therefore,

By re-arranging terms and applying equation σ zz(x, 0) = —P (derived above),

For the final boundary condition,

Now, by the definition of strain rates,


Re-arranging terms,

At the surface,

The final boundary condition follows by combining this with ) Equations (A1.5 and (A1.6) and solving for
Appendix 2 Linearization of Glen’s Flow Law
Using assumption (7) and eliminating higher-order terms, the perturbed flow law in Equations (3c) and (3d) reduces to

Now, by assumption


Again, by expanding powers and eliminating higher-order terms,

Cancelling like terms leaves

When
Appendix 3 Derivation of Lyapunov Exponent
Note that intuitively
From Equation (24),

where s and t are given in Equation (16). Note that s and t are complex conjugates, so s = a − bi and t = a + bi for some a and b. Also note a > 0 and b > 0 for all n. Both of these facts are easily proved with De Moivre’s theorem (see, for example, Reference DerrickDerrick, 1984, p. 16).
Now,

and

So define

Also note


and

and

Therefore, by simple algebra, Equation (A3.1) reduces to

By expanding all products,

Note that this function is now entirely real (no imaginary component).
In the limit as z gets large the negative exponentials will disappear. So,


The lefthand limit reduces trivially to ak, but the righthand limit oscillates between 0 and −∞. However, we are only concerned with lim sup z→∞ , so we choose 0, and

This is the Lyapunov exponent and the result we wanted to show.