Multi-decadal elevation changes of the land terminating sector of West Greenland

Abstract

Regional assessments of ice elevation change provide insight into the processes controlling an ice sheet's geometric response to climate forcing. In Southwest Greenland's land terminating sector (SWLTS), it is presumed that ice surface elevation changes result solely from changing surface mass balance (SMB). Here we test this assumption by developing a multi-decadal (1985–2017) record of elevation change from digital elevation models (DEMs) and comparing it to regional climate model output and available records of ice speed. The SWLTS thinned by >12 m on average over the full 32-year period, but the change was highly variable in time and space. Thinning was amplified in the central region of the SWLTS, relative to the north and south. During 1985–2007, the north and south regions demonstrated net thickening while the central region thinned. Regional differences in elevation change are inconsistent with SMB anomalies, indicating that enhanced ice flow in the north and south contributed to thickening during this early time interval. While clear validation in the south is prevented by incomplete velocity data, historical surface speeds in the north were elevated. These findings support the interpretation that changing ice flow can influence ice surface elevation in the slow-moving SWLTS.

1. Introduction

The rate of mass loss of the Greenland Ice Sheet (GrIS) has increased six-fold since the 1980s (Mouginot and others, 2019), amounting to a sea-level rise of 10.8 ± 0.9 mm between 1992 and 2018 (Shepherd and others, 2019). This mass loss has been driven by a combination of SMB changes and greater ice discharge. Neither SMB nor ice discharge losses have had constant rates and understanding of SMB and ice discharge partitioning has evolved with improved modeling and observations. As a result, while SMB and ice discharge contributions were equally split between 2000 and 2008 (e.g. van den Broeke and others, 2009), more recent studies have reported a greater contribution from SMB since 2009 (e.g. Enderlin and others, 2014; Shepherd and others, 2019).

Reconstruction of the ice sheet's mass changes has been accomplished using various techniques and datasets obtained by satellite altimetry (e.g. Sørensen and others, 2011; Helm and others, 2014), photogrammetric DEMs (e.g. Bolch and others, 2011), gravity analysis (e.g. Velicogna, 2009; Velicogna and others, 2014) and combined regional climate model output and ice discharge flux estimates at marine-terminating outlets ~ the ice sheet (input-output method, e.g. Mouginot and others, 2019, Rignot and others, 2011). While gravity analysis and flux-based estimates determine mass change directly, altimetric methods infer mass loss and gain. This is a complicating factor with elevation studies because surface changes may be attributed to SMB processes, firn densification and/or ice dynamics. The gravimetry method does not suffer from this issue but is limited in its ability to partition the measured mass change into the SMB and ice flow components. Indeed, the so-called mass budget method, which computes mass change from SMB and ice discharge independently, is the only method that explicitly partitions contributing sources.

Several elevation change studies have documented the ice sheet-wide changes taking place over recent decades (Csatho and others, 2014; Sørensen and others, 2018; Shepherd and others, 2019; Smith and others, 2020). Regional studies of GrIS elevation change have predominantly focused on marine-terminating sectors where dynamic thickness changes can be large, exceeding tens of meters per year (Felikson and others, 2017; Khazendar and others, 2019). In contrast, land terminating sectors of the GrIS can only lose mass by SMB processes (Sole and others, 2008). In the ablation zone of the SWLTS, firn processes have no impact on the determination of mass change from ice sheet thinning/thickening and ice flow is commonly assumed to be slow enough to have a negligible influence on geometric change (Sutterley and others, 2018). Ice sheet mass change determined from altimetry should therefore agree with other methods. However, the validity of the assumption that ice flow is an inconsequential driver of elevation change in the SWLTS remains uncertain.

Here, we test this assumption by investigating three decades of surface elevation changes across the SWLTS of western GrIS using existing DEMs. Prior studies have either focused on a few site-specific transects (Sole and others, 2008) or integrated the land terminating sector in larger ice sheet-wide studies (Csatho and others, 2014; Sørensen and others, 2018). The only regional assessment of change in this sector of the ice sheet has been based on modeled SMB (Mouginot and others, 2019). We focus on the land terminating area and include better spatial coverage and resolution from DEMs over three periods. We compare these elevation changes to SMB anomalies computed from the Regional Atmospheric Climate Model (RACMO) and interrogate historical ice flow data to determine whether the elevation changes we compute over the SWLTS during different periods can be attributed solely to SMB, or if changes in ice flow have impacted ice geometry over the study period.

2. Study domain

We define the SWLTS as extending from 65°0′N to 68°7′N (Fig. 1). While this stretch includes no marine calving outlets, the north and south delineations are approximate based on latitude and not an analysis of ice flow. Several small termini within the region are ‘wet’, meaning that they terminate in a lake, but they show no substantial calving and so we assume mass loss from ice discharge is negligible. The interior boundary of our study domain is based on data availability and does not include the entire ablation zone (refer to ELA shown in Fig. 1). The entire domain extends ~10–50 km inland and 420 km N–S, covering >5000 km² and surface elevations spanning 40 to 1370 m. We further divide the sector into three regions, a north, central and south region to explore in greater detail the regional patterns of ice thinning (Fig. 1). The delineations are subjective, broadly capturing the spatial differences in thinning we observe across the study area (see Results). In each region, we identify flowline transects along selected outlet glaciers and report changes along each: Akuliarutsip Sermia, Usulluup Sermia (North), Isunnguata Sermia (Center) and Saqqap Sermia (South).

Fig. 1. Study site (red box). The study sector has been separated into three geographic regions (N, C, S) to explore regional differences in surface elevation change in the GrIS used for Table 2. The black curves indicate central flowlines of each outlet glacier used for Table 3 and Fig. 6. The dashed line shows the Equilibrium Line Altitude (ELA) from RACMO (average 1985–2017 SMB = 0). The yellow color shows the ice cap separated from the GrIS defined by Rastner and others, 2012. The gray and blue color show the bedrock and ocean, respectively.

3. Data and Methods

3.1. Surface elevation

We used DEMs from three different sources to determine ice sheet surface elevation at four points in time during the 1985–2017 study period: AeroDEM (1985), the Greenland Ice Mapping Project DEM (GIMP) (2007) and ArcticDEM (2013 and 2017). Each of these data products was generated by different methods and has different resolutions and errors.

The AeroDEM data provide surface elevations (spatial resolution of 25 m) for southwestern Greenland in 1985 based on stereo image-pairs from aerial photographs obtained in July and August. The DEM shows an accuracy better than 10 m horizontally and 6 m vertically by co-registration to the Ice, Cloud and land Elevation Satellite (ICESat) data, while the precision is better than 4 m (Korsgaard and others, 2016). However, the DEM generation method is dependent on high-visible contrast images, which inhibits data in the low contrast areas of the upper ablation and accumulation zone where snow coverage may have persisted during the time of photography. To evaluate the quality of the data points, a reliability mask (RM) is available, which contains the Figure of Merit (FOM) values discriminated between measured and interpolated pixels. We used RM as a filter with FOM values less than 40 in the grid as outliners (Korsgaard and others, 2016).

The GIMP DEM (Howat and others, 2015, see: https://nsidc.org/data/nsidc-0645/versions/1 for reference) was generated from a combination of ASTER and SPOT-5 DEMs. The data are then horizontally and vertically registered to average ICESat elevations from 2003 to 2009, which therefore gives 2007 as a nominal date of the product. The DEM is gridded at 30 m resolution. The root mean square error of the difference between the GIMP DEM and the ICESat elevations is ±11.1–13.5 m over the study site at the ice-free area (Howat and others, 2014).

The ArcticDEM product, created from WorldView optical stereo imagery (Noh and Howat, 2015), has a 2 m horizontal resolution. Data are delivered as strips 16 to 18 km in width and 110 to 120 km in length. The accuracy of the DEM is 0.20 m in comparison with the Airborne Topographic Mapper (ATM) measurements (Noh and Howat, 2015). We used 24 strips to cover the SWLTS (Table S1). All the DEMs are from imagery acquired during February–May in 2013 and during April–September in 2017 (Table S1).

Following the method introduced by Nuth and Kääb (2011), we co-registered all DEMs to the ArcticDEM mosaic (Haga and others, 2020; Dehecq and others, 2020; Dai and others, 2019; Rastner and others, 2017), which is compiled from multiple best quality of strips that have been registered to ICESat altimetry information and provided by Polar Geospatial Center (Porter and others, 2018, see: https://www.pgc.umn.edu/data/arcticdem/), to ensure a common reference. Before applying co-registration, we re-sampled all data to 30 m resolution and re-projected them to the same reference system (map projection: WGS 84/UTM 22N, EPSG: 32622; vertical datum: WGS 84 ellipsoid). Co-registration shows shifts between the DEMs that are 3.8 ± 2.5 m in horizontal and −0.6 ± 2.3 m in z-direction. The horizontal shifts are lower than one pixel of each DEMs and were considered insignificant (von Albedyll and others, 2018; Dehecq and others, 2020).

We estimated the uncertainty of each co-registered DEM by calculating the standard error (SE) of the difference from the ArcticDEM mosaic over the stable land surface (e.g. Berthier and others, 2007; Bolch and others, 2011). We calculated the Std dev. (σ) of pixel-wise differences of each DEM from the reference and followed the common formula for determining the SE. We take SE to be representative of the regional uncertainty (e.g. von Albedyll and others, 2018):

(1)$${\rm SE} = \displaystyle{\sigma \over {\sqrt {n_{eff}} }}.$$

where, n_eff is the number of independent values within the area of concern. n_eff is a function of the total number of points (n _tot) over the area of interest, DEM pixel size (P) and distance of spatial autocorrelation (d) of the DEM in question ($n_{eff} = {{n_{tot\;\times \;}{\rm P}} \over {2d}}$) (Gardelle and others, 2013). We compute d for each individual DEM based on Moran's I autocorrelation index on elevation differences in the ice-free area (Gardelle and others, 2013). Values range from 100 to 730 m, in agreement with prior work (Bolch and others, 2011; King and others, 2017; Florentine and others, 2018; Baurley and others, 2020; Pelto and others, 2020).

DEMs from each study year were differenced to yield elevation changes over varying time periods. We estimated the uncertainty of the rate of elevation change between two DEMs, e, according to the law of error propagation (Bolch and others, 2011):

(2)$$e = \displaystyle{{\sqrt {{\rm SE}_{\rm a}^2 + {\rm SE}_{{\rm b\;}}^2 + {\rm MED}_{\rm a}^2 + {\rm MED}_{\rm b}^2 } } \over t}.$$

Here, SE_a,b and MED_a,b are the vertical uncertainty and the mean elevation difference over the ice-free area in two DEMs, respectively. t is the time interval in years between each DEM's acquisition date.

We partition surface elevation changes into components associated with SMB and a residual, reflecting the combined uncertainty and ice dynamics contributions (See Results). The SMB deviation from steady conditions (see section 3.2) was computed for each period. This SMB anomaly was subtracted from the total elevation changes calculated from DEM differencing. The resulting residual contains the influence of changing ice dynamics from steady-state flow conditions, as well as the combined uncertainty. We assume the effect of vertical crustal motion due to Glacial Isostatic Adjustment is negligible. A, Wahr and Zhong (2013) estimated it ranged from 2.7 to 4.6 mm a⁻¹, which is significantly lower than the elevation change rates we compute. We also assume the basal mass balance and internal melt rate changes are negligible (Csatho and others, 2014).

Mass changes over the study sector were calculated by assuming a constant density of 917 kg m⁻³ representative of glacier ice, since the analysis is done on the summer surface of the ablation zone.

To test the rate of elevation changes derived from DEM analysis, we compared our results against time series determined from ATM data. We used the ATM L4, Surface Elevation Rate of Change, dataset derived from repeated elevation measurements over the GrlS between 1993 and 2018 (Studinger and others, 2014). ATM L4 data contain surface elevation change rate obtained from two different campaigns. We identified crossover points within the study domain where data density was greatest and defined 1 km diameter circular areas ~ these intersecting flight lines for analysis. We averaged the surface elevation change rate within the crossover regions between two different times. Inspection over the full study sector indicated wide variability in the data density at crossover locations, with the majority of crossover points containing insufficient data to reveal detailed temporal behavior. We present the crossover point with the greatest frequency of ATM measurements in each of the three regions for comparison against the DEM analysis and also show other crossover points with reduced data density as supplemental support (Fig. S2).

3.2. Surface Mass Balance

We use SMB output from RACMO version 2.3p2 (Noël and others, 2018) with 1 km resolution to assess the magnitude and spatial variability of SMB over the study sector. SMB is calculated as the mass addition from precipitation minus meltwater runoff, sublimation and snowdrift erosion (Ettema and others, 2009; Lenaerts and others, 2012). We averaged SMB over 1985–2007, 2007–2013 and 2013–2017 to compare elevation changes based on large-scale satellite-derived observations. We also computed SMB anomalies of each period with respect to the 1960–1990 mean, assuming ice sheet equilibrium during this interval (van den Broeke and others, 2009; Csatho and others, 2014). RACMO runoff has been found to agree with in situ ablation measurements to within ~20% (van As and others, 2018; Noël and others, 2019) and RACMO SMB error has been estimated to range between 5 and 20%, depending on basin size and location (Shepherd and others, 2012). Thus, the SMB uncertainty was assumed to be 20% in this study.

3.3. Ice speed

We use ITS_LIVE (Inter-Mission Time Series of Land Ice Velocity and Elevation) velocity data (Gardner and others, 2019), which are provided by the NASA's Making Earth System Data Records for Use in Research Environments (MEaSUREs) Program. ITS_LIVE provides mean annual ice sheet surface velocity mosaics at a spatial resolution of 240 m from 1985 to 2018, derived from the full suite of Landsat 4 (1982–2001), 5 (1984–2013), 7 (1999 to present) and 8 (2013 to present) imagery. The ice velocity product we use was calculated by the autonomous Repeat Image Feature Tracking (auto-RIFT) processing chain described in Gardner and others (2018).

The ice velocity data from Landsat 4 and 5 imagery are sparser in both time and space due to the data scarcity and lower radiometric quality than Landsat 7 and 8, which influence the velocity data quality during the earlier product years. This precludes analysis of velocity changes over the full period and across the entire study sector. Consequently, we focus results on the temporal variability in ice motion along three transects, one in each of the three study regions: Akuliarutsip Sermia (North), Isunnguata Sermia (Center) and Saqqap Sermia (South). Along each glacier's central flowline we sampled data at 500 m intervals. The uncertainties we report are the native errors included in the data distribution.

4. Results

4.1. Surface elevation change

4.1.1 Total change

During the 1985–2017 period the surface elevation decreased over the entire SWLTS (Fig. 2). The magnitude of elevation change greatly exceeds the DEM uncertainty (Table 1). Ice surface elevation change averaged over the 5000 km² study area was −12.88 ± 1.60 meters ice equivalent (m i.e.), corresponding to a total mass loss of 73 Gt during the full 32-year interval. Thinning was regionally variable. The central region thinned by 16.94 ± 1.60 m i.e. on average, while the northern and southern regions thinned by 10.53 ± 1.60 m i.e. and 7.50 ± 1.60 m i.e. respectively. The enhanced thinning is not due to increased surface melt associated with a greater distribution of low elevation ice in the central region (Fig. 3a). The central and southern regions show similar elevation distributions, while the northern region is more concentrated at lower elevations (Fig. 3b). In fact, thinning in the central region was consistently greater than or equal to thinning in the northern and southern regions at all elevation bands.

Fig. 2. Total elevation changes over the study period (1985–2017). The gray color in the ice sheet shows no data.

Fig. 3. (a) 1985–2017 elevation change in north (N), central (C) and south (S) geographic regions, averaged over 100 m elevation intervals. Shading reflects Std dev. of elevation change distribution over the study period. (b) Elevation-area distribution for each geographic region in 100 m elevation bins. All elevations are from GIMP DEM.

Table 1. Statistics of the differences between the reference DEM (ArcticDEM mosaic) and the other DEMs used in this study for the investigated periods. Mean (MED), standard deviation (σ) and standard error (SE) of elevation differences over the ice-free area obtained by comparing each DEMs with ArcticDEM mosaic data.

4.1.2 Temporal patterns

The different thinning rates between the northern, central and southern regions over the 32-years motivate a detailed exploration of the temporal variations to determine if the spatial patterns arise from systematic and persistent processes or transient behavior.

To normalize elevation changes, we report elevation change as annual rates. During the first 22-year period, 1985 to 2007, the entire SWLTS experienced lower rates of elevation change than during the later periods (Fig. 4). This is also the only period in which large regions experienced ice thickening. Elevations of the north and south regions increased, on average, at rates of 0.07 m i.e. a⁻¹ and 0.25 m i.e. a⁻¹, respectively (Table 2). Averaged along the flowlines, the elevation of Akuliarutsip Sermia increased at a rate of 0.15 m i.e. a⁻¹ and Saqqaq Sermia in the south increased at a rate of 0.50 m i.e. a⁻¹ (Table 3). However, the central region which includes Isunnguata Sermia and Russell Glacier experienced thinning rather than thickening.

Fig. 4. Rates of elevation change (a, d, g), SMB anomaly with respect to the 1960–1990 mean (b, e, h) and the residual (difference between elevation change and SMB anomaly, c, f, i) during 1985–2007, 2007–2013 and 2013–2017. The gray color in the ice sheet shows no data.

Table 2. Mean elevation change rate (dH/dt) based on DEMs, SMB anomaly with respect to the 1960–1990 mean and Residual of total and individual north, central and south regions during 1985–2017.

Table 3. Mean elevation change rate of selected outlet glaciers during 1985–2017.

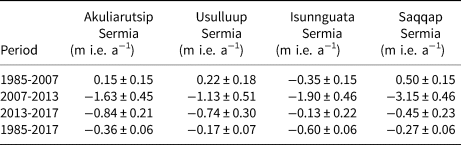
Ice thinning dominated the entire Western Greenland sector during the six-year interval from 2007 to 2013. Elevation loss occurred at an increased rate (relative to the 1985–2007 period) of −1 to −3 m i.e. a⁻¹ across the entire study sector (Fig. S3). The north and south regions switched from average thickening over all elevations in 1985–2007, to thinning at rates equivalent to the central region (Figs 4 and S3). The mean thinning rate of Akuliarutsip Sermia in the north was −1.63 m i.e. a⁻¹. The mean rate of elevation changes on Saqqap Sermia in the southern region evolved from net thickening in the early period to rapid thinning (−3.15 m i.e. a⁻¹); the largest change over the study region (Table 3).

During the final four years from 2013 to 2017, thinning continued across most of the SWLTS, but at a reduced rate relative to the prior period. For example, the mean thinning rate over the central region decreased by ~80% compared to its rate during 2007–2013. The mean thinning rate averaged across the entire sector during this period was 0.63 ± 0.16 m i.e. a⁻¹ (Table 2).

Comparing our DEM-based results with measurements from airborne laser scanning provides an independent check of the DEM analysis (Fig. 5). The areal averages from DEM differencing were compared to the single region of ATM measurements. In the central region, laser altimetry data show similar temporal changes to the DEM analysis, with relatively small ice thinning rates between 1993 and 2009 (−0.5–0.2 m i.e. a⁻¹), which increased significantly in magnitude 2009 and 2013 (−2.0–−1.2 m i.e. a⁻¹) and subsequently moderated after 2013 (−0.8–0.2 m i.e. a⁻¹) (Fig. 5f). In contrast, surface elevation in the south region increased during 1993–2001 (0.1 m i.e. a⁻¹), transitioned to rapid thinning during 2001–2014 (−1.4–−0.5 m i.e. a⁻¹) and continued to thin since 2014, albeit at a much lower rate (Fig. 5g). Whereas there is no data in the north region until 2004, we found that the elevation thinning rate was the greatest during 2005–2011 (−1.1 m i.e. a⁻¹) and declined toward the end of study periods (−0.6 m i.e. a⁻¹) (Fig. 5e). ATM error from each selected crossover time period ranged from ±0.3 m i.e. a^–1 to ±1.2 m i.e. a^–1.

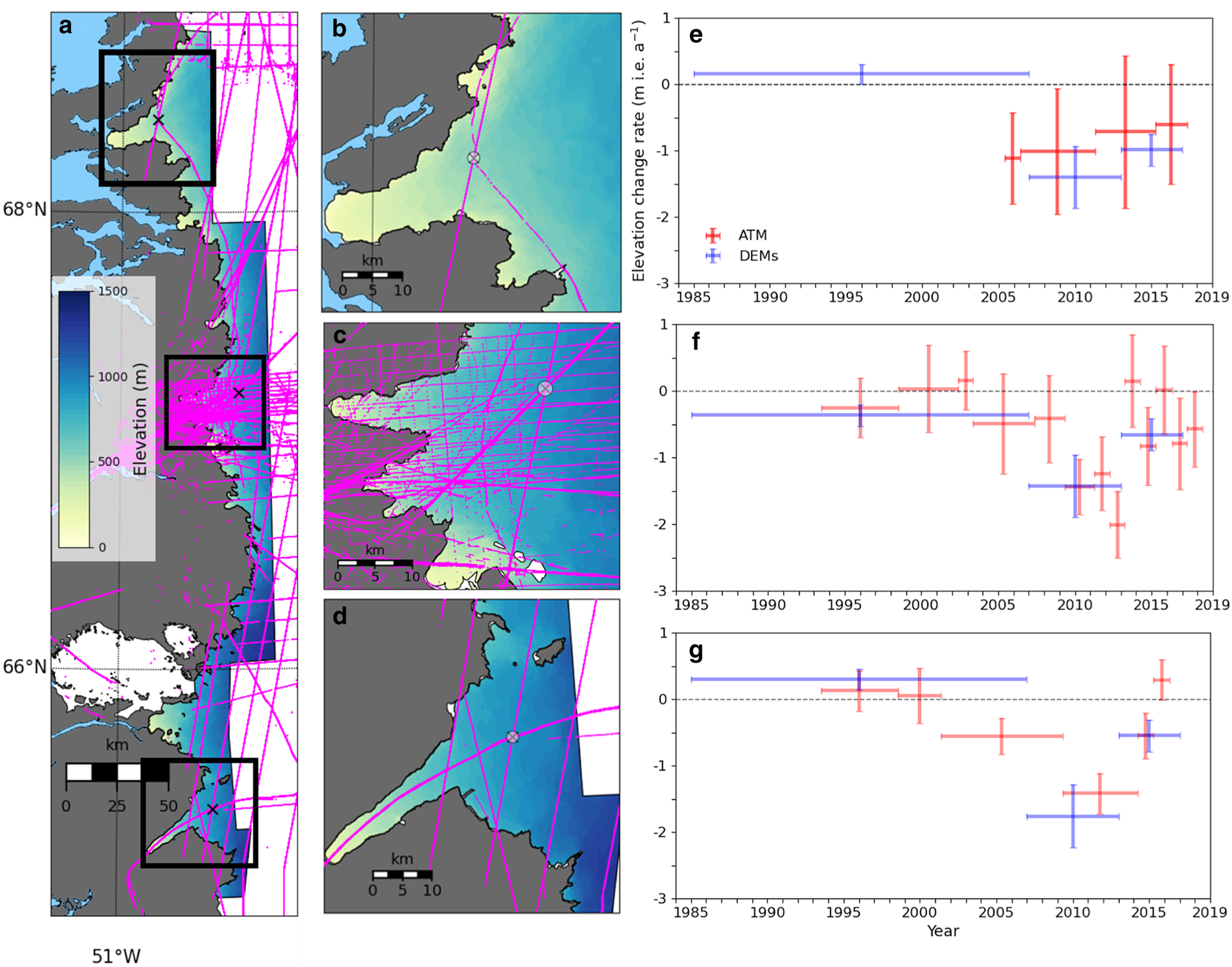
Fig. 5. IceBridge ATM flight lines from 1993 to 2018 (purple) over the study area (a), Akuliarutsip Sermia (b) Isunnguata Sermia (c) and Saqqap Sermia outlet glacier (d). Shaded circle indicates each area with the greatest number of ATM cross-overs in the study sector and is the location of the respective elevation change time series in (e–g). The elevation changes obtained from ATM data (red) and DEM analysis (blue). The uncertainty is given by the vertical error bar.

4.2. Surface Mass Balance

The average annual surface mass balances across the study sector estimated by RACMO 2.3p2 (Noël and others, 2018) show negative values as large as 5 m i.e. a⁻¹ at low elevations, which decline with increasing elevation (Fig. S4). The results show no substantial differences between the north and central regions; average thinning rates from SMB during the 1960–1990 period are nearly identical (Table S2). In contrast, ice thinning due to SMB in the south region was reduced compared to the north and south regions. The average steady state (1960–1990) SMB thinning in the south region was 1.5 m i.e. a⁻¹, more than 1.0 m i.e. a⁻¹ less than the north and central counterparts (Table S2).

The mass balance anomalies (i.e. relative to the 1960–1990 reference period), were negative across the entire study sector during each of the three intervals (Fig. 4b, e, h). However, the average SMB anomalies were very small during 1985–2007 and 2013–2017, averaging just −0.27 ± 0.05 m i.e. a⁻¹ and −0.44 ± 0.09 m i.e. a⁻¹ across the sector, respectively. A strong negative anomaly of −0.81 ± 0.16 m i.e. a⁻¹ occurred over the 2007 to 2013 interval. Annual mass balance during this interval was strongly negative, averaging −3.07 ± 0.61 m i.e. a⁻¹ across the entire study area. Interestingly, while the steady state (1960–1990) SMB pattern in the south differs from the north and central region, the SMB anomaly is uniform over the entire region for all three study periods (Table 2).

4.3. Ice speed

Ice speed displays a variable spatial pattern across the study region, reaching a peak speed of 250 m a⁻¹ at Russell Glacier (Fig. 6a). The mean ice speeds along the central flowlines of Akuliarutsip Sermia, Isunnguata Sermia and Saqqap Sermia in 2017 were 134 ± 1 m a⁻¹, 106 ± 0.2 m a⁻¹ and 145 ± 0.5 m a⁻¹, respectively.

Fig. 6. Spatial distribution of mean surface ice speed in 2017 (a). Ice speed along the central flowline (white curves) shown in Fig. 1 and its temporal variations at Akuliarutsip Sermia (b), Isunnguata Sermia (c) and Saqqap Sermia (d) during 1985–2017. Time series of mean ice speed along three transects(e). Shading regions represent the uncertainty of ice velocity. The red vertical line shows the acquisition time of the DEMs used in this study.

Assessment of changes in ice speed over the period of interest is unfortunately strongly affected by data availability. Velocity records dating back to 1985 are available at Akuliarutsip Sermia and indicate a clear and substantial slowdown over the study period (Fig. 6b). Maximum ice speed along the transect decreased from 241 ± 8 to 178 ± 1 m a⁻¹ (−26%) during 1985–2017, the largest change among the three transects. Closer to the ice margin, within 10 km of the terminus, it decelerated from 149 ± 11 to 124 ± 1 m a⁻¹ (−17%). The average ice speed along the flowline at Akuliarutsip Sermia decreased in two phases: from 1985–2000 to 2007–2013 (Fig. 6e).

At both Isunnguata Sermia and Saqqap Sermia, data limitations prevent the assessment of velocity changes before the late 1990s (Fig. 6e). From 2001 to 2017, the mean ice speed along the Isunnguata Sermia transect decreased by approximately 5–10%. At Saqqap Sermia, no discernible change in speed occurred over the same period.

5. Discussion

5.1 The role of ice flow in determining elevation change

Our analysis reveals varying spatial and temporal patterns in thinning over the 32-year record and a complex relationship to SMB patterns. If ice flow was a negligible factor, then our calculated elevation change rates should mimic SMB anomalies. Our results show that this is not the case in any measurement period. Rates of elevation change computed during 1985–2007 are consistent with the SMB anomalies in the central region, but while the SMB anomalies in the north and south regions were similar to the central area, these regions experienced net thickening. The residual in North and South region were 0.36 ± 0.14 m i.e. a⁻¹ and 0.52 ± 0.14 m i.e. a⁻¹ during the period, respectively (Table 2). During 2007–2013, thinning rates are largely elevated from SMB anomalies in all regions and this discrepancy is also found in the most recent 2013–2017 period.

The discrepancies between elevation change rates and SMB anomalies indicates that ice flow has a nonnegligible impact on ice sheet elevation change. However, other factors inherent to available datasets complicate this interpretation. For instance, the DEMs collected in 2013 are from February to May, while those in 2017 reflect elevations in July–August (Table S1). Thus, the nominal four-year period captures five melt seasons. Such DEM timing differences can bias the calculated elevation change rates, especially in this study region where summer melt rates are the some of the largest on the ice sheet (Ettema and others, 2009). This makes it challenging to draw robust conclusions regarding the role of ice flow in controlling elevation change in our study sector over the most recent and shortest time intervals.

Nevertheless, the total elevation change we calculated over the SWLTS during the 32 years is robust and indicates that the central region had amplified elevation loss relative to the north and south. The greater thinning was due to the 1985–2007 period, yet SMB anomalies during this time were consistent across the entire study sector. In the absence of regional differences in SMB anomalies, such a discrepancy can only arise from regional differences in ice flow patterns. Flow rates in the north and south regions must have been elevated during this period, contributing to thickening despite a negative SMB anomaly.

The ITS_LIVE (Gardner and others, 2019) ice flow speeds confirm that outlets in the northern region experienced elevated ice speeds in the early period. This is consistent with historical observations, which indicated readvance of Akuliarutsip Sermia between 1950 and 1985 (Weidick, 1994). Deceleration of ice speeds since the early-mid 2000s was also shown by Tedstone and others (2015) and Williams and others (2020) and interpreted to reflect long term subglacial drainage evolution in response to changing melt conditions.

Further south data availability issues prevent a clear and obvious relation between changing ice flow and surface elevation. Ice thickening was previously identified at Saqqap Sermia in the southern region during the 1993–1998 using ATM measurements (Abdalati and others, 2001; Thomas and others, 2009). Huybrechts (1994) suggested that this broad sector of the ice sheet was still responding to the ice sheet's re-advance since the Holocene climatic optimum, causing net thickening. The modeling study provides indirect evidence supporting historical thickening associated with changing ice flow.

The above illustrates a complex ice flow history in SWLTS that reflects a response to potentially different process forcings acting over a range of time scales. In this context, the regional variation in elevation changes during the1985–2007 period is perhaps unsurprising. Yet, it does contradict the finding that elevation changes in land terminating regions follow SMB patterns (e.g. Sutterley and others, 2018); a finding supported by earlier work in the same study area (Sole and others, 2008). There, however, remain some important differences between our study and that of Sole and others (2008), which help clarify this apparent disagreement. Sole and others (2008) concluded that there was no statistical difference between elevation change rates and SMB anomalies on select land terminating transects. However, their analysis neglected cases of ice thickening, whereas thickening in the southern and northern regions is precisely the source of the variability we identify over our study sector. Furthermore, Sole and others (2008) included both land and marine-terminating outlets in their analysis, with changes on land terminating glaciers small compared to the more severe dynamic thinning occurring in the marine setting. Our study focuses on the land terminating sector alone and addresses elevation changes that are relatively minor compared to the dynamic thinning/thickening rates on some fast-flowing marine outlets, which can be an order of magnitude larger than SMB-driven thinning. When considering the land-terminating sector in isolation, our findings also caution against the finding that elevation changes only reflect SMB.

6. Conclusions

Our DEM-based assessment of elevation changes over a 5000 km² portion of the ablation zone along the SWLTS is the first such region-specific analysis of decadal geometric evolution. It contributes to efforts to document GrIS change through altimetric, gravimetric and mass budget methods. Overall, the entire sector thinned, lowering the surface by an average of −12.88 ± 1.60 m i.e. over the 32 years from 1985 to 2017. However, neither the temporal nor the spatial patterns of surface lowering were uniform across the sector. The thinning in the central region of the study sector is nearly double that of the counterparts to the north and south.

The regional variations in thinning across the study area arise during the 1985–2007 interval, when the central region thinned while both the north and south regions thickened. We find that this result cannot be attributed to SMB anomalies, according to the RACMO regional climate model. This implies that ice flow changes have had a measurable impact on ice geometry; a finding supported by available ice velocity data. The mechanism(s) behind the regional variability in ice flow implied by our analysis is unclear, but there is evidence that the SWLTS has undergone complex changes in ice flow from multiple processes and across time scales ranging from multi-annual to millennial. Our results suggest that these changes in ice flow can impact ice sheet elevation and show that even in relatively slow moving, land terminating regions of the GrIS, mass change cannot be assumed to be equal to SMB anomalies.