1. Introduction
One long-standing problem in snow avalanche science is to find a constitutive model for flowing snow that describes the viscous, plug-like motion of wet snow avalanches as well as the highly sheared, collisional behaviour of dry snow avalanches. Ideally the model would explain how surface roughness and snow properties influence the flow regime and predict the formation of a powder-snow avalanche from a dense flowing avalanche. To reach this goal the constitutive model must account for the complex interaction of the avalanche with the basal running surface while reconciling macro-viscous and micro-granular descriptions of the flow.
In this paper, we address this problem by deriving relationships between the random motion of snow granules and the energy dissipation in avalanches. These relationships are analogous to ‘fluctuation-dissipation’ relations which are commonly used to describe multi-degree-of-freedom systems with random movement (e.g. Brownian motion; Reference LemonsLemons, 2002). They allow a macroscopic description of the microscopic energy dissipation which, in the case of snow avalanches, arises from the random inelastic collisions and enduring frictional rubbing between snow granules. As such, fluctuation-dissipation relations are a tool to study not only viscous/collisional flow regimes but also how the random motion of the granules, the granular agitation, affects the overall stability of the avalanche in response to boundary conditions, such as external disturbances arising from the terrain roughness.
However, fluctuation-dissipation relations cannot be derived without first identifying the source of the granular fluctuations and then examining how these fluctuations are destroyed. This problem necessarily involves studying how the potential energy driving the flow is transformed into kinetic energy – both translational and random kinetic energy – and finally to heat. Our study is motivated by the fact that the generation of heat and fluctuation energy at a rough bottom boundary are competing processes, since the sum of the two must be equal to the potential energy remaining after the viscous shearing has been overcome in the avalanche core. In order to maintain steady state, the dissipated energy will be exactly the difference in potential energy required to maintain a constant flow speed. We therefore investigate the fluctuation energy input required to maintain steady-state flows, first using a simple block model and then using a more realistic depth-averaged model containing internal deformations. In this analysis we consider depth-averaged mechanical work rates – and not flow forces as is customary in avalanche science – since they can be directly and more easily linked to changes in random kinetic energies of the granules.
The most important result described in this paper is that the fluctuation–dissipation relations place restrictions on constitutive formulations describing snow avalanche flow. Firstly, the constitutive model for the frictional stresses at the basal boundary cannot be chosen independently of the constitutive model governing the dissipative processes at higher levels in the avalanche profile. Secondly, the mutual interaction between the viscous and collisional processes must be reciprocal and therefore cannot be described by ad hoc constitutive ideas. To clarify these points we apply our results to develop a constitutive model for snow avalanches which contains the three interacting dissipative mechanisms: basal slip, viscous shearing and inelastic granular collisions (see Fig. 1). The fluctuation energy (‘granular temperature’) is introduced as an independent state variable, in a similar way to continuum theories of granular flow (Reference HaffHaff, 1983; Reference Jenkins and SavageJenkins and Savage, 1983; Reference Hutter, Szidarovszky and YakowitzHutter and others, 1987; Reference Hutter and RajagopalHutter and Rajagopal, 1994; Reference Louge and KeastLouge and Keast, 2001; Reference Aranson and TsimringAranson and Tsimring, 2002; Reference LougeLouge 2003). We are able to model the measured steady-state velocity profiles of both wet and dry snow avalanches and explain observed phenomena such as the large shear rates near the basal layer. Although our formulation describes the full range of snow flows, more experimental work is needed to advance more precise constitutive formulations.

Fig. 1. Top: The granular deposits of a large snow avalanche released at the Swiss Valiee de la Sionne test site. The snow granules are 10–20cm in size. Bottom: The basal sliding surface of a large snow avalanche. Note the shining ice layer produced by basal friction. The ice layer is several millimetres thick. A shovel is located at the right of the bottom picture. Such observations indicate that basal sliding, viscous shearing and inelastic collisions are the primary energy-dissipation processes.
2. Random Fluctuations In Depth-Averaged Avalanche Flow
In this section we consider how random granular fluctuations affect the energy balance of steady-state flows in simple avalanche models. We start by considering the energy conservation of a sliding block slipping down an inclined plane. For any given inclination, the block reaches a steady velocity and thus a constant energy-dissipation rate. To study the energy balance, we use a coordinate system that is moving with the centre of the mass of the block (Lagrangian coordinates). This simple description of avalanche flow corresponds to the so-called Voellmy–Salm model, which has been used extensively to predict snow avalanche run-out distances (Reference SalmSalm, 1993). It does not explicitly account for the internal deformations in the avalanche body. The force opposing gravity is modelled as ‘friction’ on the ground, at the interface between the moving block and sliding surface. Thus, the sliding-block model contains the first important component in our analysis: friction at the basal surface. It allows us to define the balance between the gravitational work rate and rise in internal energy in steady-state flow.
The sliding-block analysis facilitates the introduction of the two other important dissipative processes: granular collisions and viscous shearing in the avalanche core in a depth-averaged model with a sheared velocity profile. We still consider the energy balance since this procedure allows us to determine the frictional work done by the random processes and identify where the random kinetic energy is generated. This result cannot be obtained by postulating constitutive relations for the internal and boundary stresses directly, as is customary in avalanche science (Reference Dent and LangDent and Lang, 1983; Reference Norem, Irgens and SchieldropNorem and others, 1987; Reference NishimuraNishimura, 1990; Reference SalmSalm, 1993; Reference Bartelt, Salm and GruberBartelt and others, 1999). A list of the necessary notation is provided in Tables 1–3.
Table 1. Avalanche coordinates and parameters

Table 2. Energy, work and dissipation. If the quantity is encountered with a double prime (e.g. K”), the units are J m–2; triple prime units are J m–3. Dotted values represent rate of change (e.g. Wg is the gravitational work rate with units W)

Table 3. Constitutive parameters

2.1. Sliding-block model, no internal deformations
The ‘avalanche’ (Fig. 2) consists of a mass of snow at elevation H(x) moving down a slope of constant angle, ϕ = arctan (dH/dx). The avalanche is in steady state and the bulk flow density, p, and the velocity, u(z), are not only constant in time, t, but are also independent of z; that is, u(z) = um, the mean velocity. A volume slice has thermal temperature T, which is continuously increasing due to the frictional processes. For the flow volumes 1 and 2 depicted in Figure 2, the translational kinetic energy K(um), the potential energy Ug(H) and the internal energy E(T) can be defined.

Fig. 2. Avalanche flow in steady state, sliding-block model. The kinetic energy of the avalanche does not change, but the internal energy, E, increases from position 1 to 2. The system is therefore in thermodynamic non-equilibrium.
If we compare the energies and temperatures of the avalanche at positions 1 and 2, we find that, by definition of steady state, the translational kinetic energy K(um) is constant and therefore the change in kinetic energy ΔK = 0. The potential energy of the considered snow volume at position 1, Ug(H), has changed by descending the distance AH, the difference in elevation H2 — H1. The change in potential energy is denoted ΔU g. The internal energy of the avalanche, E, changes as well when moving from 1 to 2 by ΔE. Energy conservation demands that the sum of the changes of kinetic, potential and internal energies be zero:
Since the kinetic energy is constant in steady state, we have
In other words, the decrease in potential energy of the volume slice must be equal to the increase in internal energy of the slice. Considering a slice of unit width and length and of height h, we can equivalently write
which is the same equation as Equation (2), expressed per unit flow area. (A double prime denotes a quantity per unit area; a triple prime a quantity per unit volume.)
The concept of conservative and non-conservative forces can be effectively applied to find the relation between the gravitational work rate and the dissipation rate. The total change in translational kinetic energy (which must be zero in steady state) can be divided into two parts:
The quantity ![]() represents the change (gain) in translational kinetic energy due to the conservative gravity force (subscript ‘g’). The loss in kinetic energy due to the nonconservative friction forces is denoted
represents the change (gain) in translational kinetic energy due to the conservative gravity force (subscript ‘g’). The loss in kinetic energy due to the nonconservative friction forces is denoted ![]() . In our elementary sliding-block model there is only one nonconservative process: the friction at the basal layer, which we denote with the subscript ‘B’. Therefore, the loss in kinetic energy is due entirely to basal sliding,
. In our elementary sliding-block model there is only one nonconservative process: the friction at the basal layer, which we denote with the subscript ‘B’. Therefore, the loss in kinetic energy is due entirely to basal sliding,
Applying the work-energy theorem to the conservative and non-conservative subsystems leads to:
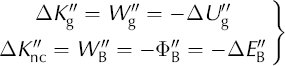
where ![]() is the mechanical work done by gravity,
is the mechanical work done by gravity, ![]() is the frictional work done by the non-conservative forces at the basal slip layer and is the dissipated work at this layer. Because
is the frictional work done by the non-conservative forces at the basal slip layer and is the dissipated work at this layer. Because ![]() in steady state, we have from Equation (6),
in steady state, we have from Equation (6),
the conservative and non-conservative work done must balance, or
all the gravitational work goes into raising the internal energy of the block, or, the gravitational work rate, ![]() , is equal to the dissipation rate,
, is equal to the dissipation rate,
![]() , at the basal surface,
, at the basal surface,
Because we are using a simple block model without internal deformations or kinetic energy fluctuations, the increase in internal energy corresponds to a heat source, raising the temperature at the basal sliding surface.
2.2. Depth-averaged model
In order to see how the balance between potential energy change and internal energy rise is affected by a velocity profile, we now introduce internal deformations: viscous shearing and granular fluctuations in the bulk (Fig. 3). Since we are considering variations in z, the sliding-block control volume with height h (Fig. 2) is partitioned into small intervals, dz (Fig. 3). As the density, p, is assumed to be isotropic and constant, there is no change in the height of flow, h, which therefore remains the same in both the rigid sliding-block and deforming body descriptions. The other quantities will depend on z. Each volume element of height dz will have the same difference in potential energy ΔU, but not the same difference in internal energy ΔE, which depends on the velocity gradient as well as the fluctuation energy distribution of the granules F(z,t). We neglect spatial changes in ΔE due to heat transfer mechanisms, such as thermal heat conductivity.

Fig. 3. Avalanche flow in steady state. The avalanche is no longer a sliding block, but moves with an internal velocity profile u(z). The mean velocity of the avalanche is um. The mass flux at height z is M(z).
Of course, u m still corresponds to a mean velocity defined such that the total mass flux is preserved (see Fig. 3). The mass flux at height z per unit flow area is
To find the mean velocity we simply integrate u(z) over the flow height

so that we can remove the z dependency on the velocity.
Energy conservation still demands that the sum of the changes of kinetic, potential and internal energies per unit cross-sectional area be zero:
The fluctuation energy, F″(t), is considered a random stochastic kinetic energy and a function of the time, t. The internal energy, E″(t), is also a function of time because it is continually increasing, whereas the changes in translational kinetic energy and potential energy are constant in our steady-state system. The total change in translational kinetic energy can be decomposed, as before, into conservative (gravity gains) and non-conservative parts. In contrast to the sliding-block model, however, the non-conservative change in kinetic energy now contains additional contributions (losses) arising from the viscous shearing and inelastic collisions within the core of the avalanche:

The changes ![]() are the depth-integrated losses of translational kinetic energy due to viscous shearing and inelastic collisions:
are the depth-integrated losses of translational kinetic energy due to viscous shearing and inelastic collisions:

and

The fluctuation energy, F’” (z), represents the kinetic energy of the random velocity fluctuations:
where f(z) is the mean-square velocity of the granular fluctuations. Although K(z) and F(z,t) are both kinetic energies, they represent two entirely different processes. The root-mean-square velocity, ![]() , represents the random fluctuating velocity which is superimposed on the translational velocity of the mass flow. As the sum of the squares of the fluctuating velocity of each particle, it is a positive function. Consequently, the random kinetic energy, F(z,t), is not zero. However, the sum of the fluctuation velocities must be zero since each fluctuating motion has a counterpart in the opposite direction. The random system can have no bias because the mean translational velocity is defined such that any possible bias will be zero. The velocity is divided into a systematic part and noise. The ensemble average of the noise vanishes, but the ensemble average of the systematic part remains.
, represents the random fluctuating velocity which is superimposed on the translational velocity of the mass flow. As the sum of the squares of the fluctuating velocity of each particle, it is a positive function. Consequently, the random kinetic energy, F(z,t), is not zero. However, the sum of the fluctuation velocities must be zero since each fluctuating motion has a counterpart in the opposite direction. The random system can have no bias because the mean translational velocity is defined such that any possible bias will be zero. The velocity is divided into a systematic part and noise. The ensemble average of the noise vanishes, but the ensemble average of the systematic part remains.
2.3. Fluctuations and mechanical work
The mechanical work done by the random frictional forces arising from the particle fluctuations is

where ![]() is the resultant frictional force of the random collisional processes per unit area in the × direction. The mean value, in time, of the integral in Equation (17) is zero, due to the irregularity of the random forces, Rr(t),
is the resultant frictional force of the random collisional processes per unit area in the × direction. The mean value, in time, of the integral in Equation (17) is zero, due to the irregularity of the random forces, Rr(t),
Thus, like the fluctuating velocities, the force ![]() averaged over time must be zero, since it arises from a random process and, as such, is a function of time but without bias, meaning that it is indifferently positive or negative. Thus, the collisional and fluctuating motion of the snow granules produces heat, but does no frictional work – in the depth-averaged mean over time – against the translational motion of the avalanche. The translational kinetic energy is not influenced by the random kinetic energy,
averaged over time must be zero, since it arises from a random process and, as such, is a function of time but without bias, meaning that it is indifferently positive or negative. Thus, the collisional and fluctuating motion of the snow granules produces heat, but does no frictional work – in the depth-averaged mean over time – against the translational motion of the avalanche. The translational kinetic energy is not influenced by the random kinetic energy, ![]() . That is, the random particle fluctuations can neither accelerate nor decelerate the flow and therefore the mechanical work
. That is, the random particle fluctuations can neither accelerate nor decelerate the flow and therefore the mechanical work ![]() .
.
A similar argument was first used in the study of Brownian motion of a particle of known dimension in a viscous liquid (Reference LangevinLangevin, 1908). It is fundamental in the derivation of the fluctuation-dissipation theorem of non-equilibrium statistical mechanics (Reference LemonsLemons, 2002). The fact that the work done by the granular fluctuations is zero should not be interpreted to imply that the granular fluctuations are unimportant. On the contrary, the granular fluctuations produce a collisional stress which decreases the viscous shearing forces and thus indirectly changes the frictional work, ![]() . Equation (17) indicates that only the viscous shearing forces, at the base of the flow and within the core, can induce a change in kinetic energy directly,
. Equation (17) indicates that only the viscous shearing forces, at the base of the flow and within the core, can induce a change in kinetic energy directly, ![]() . We conclude that the viscous shearing and the granular interactions can be considered complementary descriptions of the same effect (Reference LangevinLangevin, 1908), that is, the heating of the avalanche core.
. We conclude that the viscous shearing and the granular interactions can be considered complementary descriptions of the same effect (Reference LangevinLangevin, 1908), that is, the heating of the avalanche core.
2.4. The source of fluctuation energy
A further consequence of Equation (17) is that, in steady state, the depth-integrated mean fluctuation energy, F″, must remain constant. Hence, both ΔK″ and ΔF″ must be zero, ΔK″ = 0 and ΔF″ = 0. The integrated increase in potential energy is transformed, as before, into internal energy or heat. If a source of fluctuation energy exists, it must be balanced by an internal energy sink, such that ΔF″ = 0. The gravitational work done must balance the change in internal energy:

But the gravitational work must also be in balance with the frictional work done by the non-conservative processes in steady state (cf. Equation (6))
with

The essential problem, however, in granular avalanche flow is that the heat energy produced by the granular collisions is definitely non-zero and must be accounted for in the internal energy balance

The fact that work done by the collisions is zero (Equation (17)), ![]() , but the heat produced by the collisions is non-zero (Equation (22)) disrupts the symmetry of the fundamental equation balancing the heat produced (Equation (19)) and the work done by the frictional forces (Equation (21)) in steady-state flow. The work balance relation
, but the heat produced by the collisions is non-zero (Equation (22)) disrupts the symmetry of the fundamental equation balancing the heat produced (Equation (19)) and the work done by the frictional forces (Equation (21)) in steady-state flow. The work balance relation ![]() becomes
becomes


Since the viscous work done must be in balance with the heat produced by viscous shearing,

we have

This equation can be written as a rate equation in terms of ![]() , the rate of change in internal energy, or
, the rate of change in internal energy, or ![]() , the dissipation rate due to random collisions in the avalanche body, by simply dividing the above equation by the time interval, Δt,
, the dissipation rate due to random collisions in the avalanche body, by simply dividing the above equation by the time interval, Δt,

Defining
we can write

This equation states that, in steady state, the difference between the frictional work rate, — ![]() , at the basal surface and the heat production rate at the basal surface,
, at the basal surface and the heat production rate at the basal surface, ![]() , is equal to the heat production rate by collisions or, alternatively, to the dissipation rate of fluctuation energy in the core of the avalanche. We have denoted this difference
, is equal to the heat production rate by collisions or, alternatively, to the dissipation rate of fluctuation energy in the core of the avalanche. We have denoted this difference ![]() since it physically represents the flux of fluctuation energy injected at the basal boundary. In steady state, the frictional work rate at the basal layer can only be transformed into two possible energies: internal heat energy or mechanical fluctuation energy since there can be no increase or decrease in the translational kinetic energy. The input of fluctuation energy at the basal sliding layer is subsequently consumed or dissipated in the core of the avalanche. The competition at the basal layer between friction and the creation of random fluctuation energy is the dominant process in avalanche flow.
since it physically represents the flux of fluctuation energy injected at the basal boundary. In steady state, the frictional work rate at the basal layer can only be transformed into two possible energies: internal heat energy or mechanical fluctuation energy since there can be no increase or decrease in the translational kinetic energy. The input of fluctuation energy at the basal sliding layer is subsequently consumed or dissipated in the core of the avalanche. The competition at the basal layer between friction and the creation of random fluctuation energy is the dominant process in avalanche flow.
2.5. Fluctuation-dissipation relations
The results from the depth-averaged models can be summarized as follows:
-
1. In steady state the input of mechanical fluctuation energy at the base of the avalanche is in balance with the dissipation rate of fluctuation energy in the core (conservation of fluctuation energy)
(30)
This conclusion is a direct consequence of the fact that the collisional work done against the motion of the avalanche is zero.
-
2. The input of fluctuation energy at the base of an avalanche is bounded by the basal work rate
(31)
The difference between the basal work rate and the mechanical fluctuation energy is the heat produced at the base of the avalanche
 .
.
The first result indicates that fluctuation energy must be conserved in steady-state flow. In the end, the mean mechanical work done by the change in potential energy goes partly into acceleration, raising the translational kinetic energy, and partly into ‘turbulence’, increasing the fluctuation energy, which finally goes into internal energy, raising the thermal temperature of the system. However, the total (depth-integrated) difference of potential energy and internal energy will still be equal, since the kinetic energies K″ and F″ are constant.
The second point has practical significance in avalanche engineering. The work rate at the base of the avalanche is given by
where T B is the basal shear stress and uB is the basal slip velocity. Different formulations for T B can be found in Reference Bartelt, Salm and GruberBartelt and others (1999). The constitutive relation for T B, which describes the basal work rate, bounds the fluctuation energy source at the basal sliding layer.
If the basal slip velocity vanishes, u
B = 0, then the basal fluctuation energy input, ![]() , likewise vanishes since the basal work rate
, likewise vanishes since the basal work rate ![]() . However, when
. However, when ![]() , the integral of collisional dissipation in the core of the avalanche is zero:
, the integral of collisional dissipation in the core of the avalanche is zero:

The importance of this statement is that collisional dissipation (and therefore granular fluctuations) can only exist in steady-state flow when there is a non-zero slip velocity at the basal plane.
3. Constitutive Model
3.1. Constitutive restrictions imposed by fluctuation-dissipation relations
We will now demonstrate how the ideas developed in the previous section can be used to construct a constitutive model for snow avalanche flow. The constitutive formulation must mathematically satisfy the following: (1) Only the viscous shearing forces can induce a change in kinetic energy (velocity) since the random particle collisions can neither accelerate nor decelerate the flow. (2) The random collisional interactions and the viscous shearing are complementary processes in the sense of Reference LangevinLangevin (1908). The collisional and viscous shearing stresses induced by these processes are therefore additive. (3) When using a kinetic theory we are not free to choose the constitutive models for the basal sliding and the avalanche core independently. They are mathematically linked by the slip velocity: in steady state, the input of mechanical fluctuation energy at the sliding surface of the avalanche must be in balance with the dissipation of fluctuation energy in the core.
3.2. Constitutive equations
The following constitutive equations for simple shear flows satisfy the above requirements:


where p is the effective pressure (i.e. the pressure transferred through the solid granular matrix and causing friction), p is the internal friction parameter associated with the effective pressure, v is the shear viscosity, λ is the longitudinal viscosity, p is the dispersive pressure coefficient and m, n and r are positive material constants.
The effective pressure concept ensures that the collisional and viscous stresses are complementary since the effective pressure, p(z), is defined as the sum of the normal and collisional stresses. The collisional stresses are directly related to the fluctuation energy, fz), by the dispersive pressure coefficient, η. Thus, the constitutive parameter η is a measure of how effective the agitated granules are at translating fluctuation energy into a normal stress in the z direction. The magnitude of η depends on the inelasticity and geometry of the granular material. Reference Norem, Irgens and SchieldropNorem and others (1987) have proposed a constitutive model for snow in which the effective pressure also contains a collisional stress component, but one which is a function of the shear gradient. In comparison, our constitutive model states that the effective pressure is directly a function of the fluctuation energy, fz).
The exponents m and r define the fundamental nature of the flow. For m = r = 1 we have a Newtonian fluid; for m = r = 2 we have a Bagnold fluid. Both m = r = 1 (Reference Dent and LangDent and Lang, 1983) and m = r = 2 (Reference Norem, Irgens and SchieldropNorem and others, 1987) and combinations (Reference NishimuraNishimura, 1990) have been proposed to model snow flows. In the following we will take m = r = 1, following the kinetic theory approach of Reference Jenkins and SavageJenkins and Savage (1983). We have investigated formulations with n = 1/2, n = 1 and n = 3/2 but in the remainder of the paper consider only the n = 1 case, since it was impossible to distinguish between the different formulations in our numerical calculations. A physical motivation behind this choice is that in kinetic gas theory the pressure is proportional to the fluctuation energy, i.e. n = 1.
The shear dissipation rate is:

and the normal dissipation rate is ϕ

The normal dissipation rate is zero in steady state. The total energy dissipation rate ![]() in the core of the avalanche is given by the sum of the viscous shear Equation (38), viscous normal Equation (39) and collisional parts:
in the core of the avalanche is given by the sum of the viscous shear Equation (38), viscous normal Equation (39) and collisional parts:
The collisional dissipation rate, ϕis defined in section 3.3.
3.3. Diffusion and dissipation of fluctuation energy in the core
Once fluctuation energy is created at the basal layer, it diffuses upwards into the core of the avalanche. Although this kinetic energy is, in principle, free and reversible for each snow granule, it is doomed to be irreversibly destroyed by random binary collisions. The shearing motion between the snow granules in the core can create additional fluctuation energy, but in steady state the overall balance between the basal source and collisional dissipation will remain. This condition can be enforced by solving the stationary diffusion equation conserving fluctuation energy:

with the boundary conditions at the base z = B

and at the top surface z — h (see Fig. 3)

The coefficient K governs the diffusive energy transport and is similar to the thermal conductivity in that it linearly relates the flux of fluctuation energy, Q”, to the fluctuation energy gradient,
We propose that the collisional dissipation be given by

The first term on the righthand side accounts for the destruction of fluctuation energy by granular collisions. Using statistical mechanics arguments, Reference Jenkins and SavageJenkins and Savage (1983) found

for rapidly sheared granular flows, where d is the granule diameter and e is the coefficient of restitution of the particles. The parameter α controls the penetration depth of the fluctuation energy in the core of the avalanche. The second term on the righthand side of Equation (45) represents a source of fluctuation energy arising from the shearing motion of the granules. As we show in section 3.4, this term ensures that the interaction of the viscous and collisional processes is defined by a single dissipation mechanism. The third term in Equation (45) accounts for the destruction of the fluctuation energy as a function of the overburden pressure. It contains the product of the normal stress σzz (z) and the velocity gradient, both of which vary as a function of depth. Thus, relatively more fluctuation energy is destroyed near the basal layer, where the overburden stress and shear rates are largest, than at the free surface of the avalanche where both the normal stresses and shear gradients are zero.
Many constitutive models for snow avalanche flow distinguish between active and passive flow states that account for different amounts of dissipation depending on the longitudinal strain state within the avalanche body (Reference Savage and HutterSavage and Hutter, 1989; Reference SalmSalm, 1993; Reference Bartelt, Salm and GruberBartelt and others, 1999). Usually simple soil mechanics relations are used to define the active/passive pressure coefficients. In our proposal, longitudinal strain gradients can create and destroy fluctuation energy. Note that when ∂u/∂x < 0, Equation (45) predicts that fluctuation energy is destroyed (passive state);whereas when ∂u/∂x > 0 fluctuation energy is created (active state). Thus, the last term in Equation (45) (cf. Equation (39)) provides a physical mechanism to destroy fluctuation energy when an avalanche is decelerating, for example in the run-out zone, where passive flow states are encountered. Conversely, just after snow-slab release, active flow states are encountered with increasing fluctuation energy.
3.4. Reciprocity of viscous and collisional interactions
The viscous and collisional description of avalanche motion is complementary and therefore contains interacting processes. As we have seen, the collisional fluctuation energy reduces (and therefore interacts with) the viscous shearing in the avalanche core. Likewise, the shearing motion within the avalanche core creates fluctuation energy. Both interacting mechanisms are irreversible and therefore dissipate energy. The mathematical description of the energy dissipation thus contains products of the shear strain rate (representing the viscous description) and fluctuation energy (representing the collisional description). The product must describe a single heat-producing mechanism, independent of the order of multiplication, otherwise the mathematical description allows non-unique dissipative processes. A constitutive formulation containing a complementary viscous and collisional description requires that the mutual interaction of the dissipative processes be unique and therefore reciprocal.
To clarify this idea, consider the total energy dissipation rate (Equation (40)) in the core of the avalanche. Let the symbols Xv, Xr and Xn denote the viscous shear, collisional and viscous normal processes which are defined in terms of the shearing and normal strain rates as well as the mean fluctuation velocity:

The total dissipation equation (Equation (40)) can be written as a quadratic equation in Xv, Xr and Xn. The associated matrix form is
where [L] is the matrix of the quadratic form:

The symbol ![]() denotes
denotes

The advantage of writing the total dissipation as a quadratic form is that we can identify the symmetry of the interacting processes. The constitutive formulation is such that Lij = Lji, (the subscripts i and j denote processes v, r or n). Moreover,
and
Therefore, ![]() . Similarly,
. Similarly, ![]() . The interacting processes are constructed such that they are independent of the order of the product between Xr
and Xv (or Xr
and Xn
). That is, the description of the collisional and viscous shearing interaction (or collisional and viscous normal interaction) dissipates equal amounts of energy. If Lij
= Lji, did not hold, the energy dissipation of the system would not be uniquely defined.
. The interacting processes are constructed such that they are independent of the order of the product between Xr
and Xv (or Xr
and Xn
). That is, the description of the collisional and viscous shearing interaction (or collisional and viscous normal interaction) dissipates equal amounts of energy. If Lij
= Lji, did not hold, the energy dissipation of the system would not be uniquely defined.
Another feature of the constitutive formulation is that the dissipation can be written as
where Jvi, J r and Jn are:
Note that the diagonal components of matrix [L] are constant and satisfy the condition that

Therefore, the constitutive formulation is linear in Xvi, X r and X n.
3.5. Basal source of fluctuation energy,  , the ‘slip volume’ and the ‘fluidized layer’
, the ‘slip volume’ and the ‘fluidized layer’
At the base of the avalanche, there is a boundary layer between the fixed ground and the moving bulk of snow. The granules within this layer collide with the roughness of the fixed ground with their corresponding downslope velocity. The thickness of this boundary layer is not yet defined. However, in this layer two processes must occur: the inelastic part of the collisions, including the sliding motion between the particles, will be converted to heat whereas the elastic part of the collision will be transformed into kinetic energy (Reference Hui, Haff, Ungar and JacksonHui and others, 1984; Reference Gutt and HaffGutt and Haff, 1991; Reference JenkinsJenkins, 1992). The transformation of collisional elastic strain energy to kinetic energy of the particles might extend over several diameters because of the closeness and enduring contacts of the particles. In the mean there must exist a distance from the bottom at which the mean-square velocity of the fluctuations is a maximum and the stored elastic strain energy is a minimum. This distance defines the thickness of what we call the slip volume and the location of the slip velocity, uB (see Fig. 4). As long as the avalanche is moving, fluctuation energy will be produced within the slip volume and diffused into the core of the avalanche where it is eventually destroyed. The diffusion length characterizes the thickness of the so-called fluidized layer (see Fig. 4). Within this diffusion layer the fluctuation energy produced in the slip volume is destroyed (transformed into heat energy).

Fig. 4. Frictional/collisional avalanche flow. Definition of the ‘slip volume’, the source of agitation, and the ‘fluidized layer’ where fluctuation energy is destroyed. The basal work rate, ![]() , is divided into heat,
, is divided into heat, ![]() , and granular agitation,
, and granular agitation, ![]() . In steady state the basal source is in balance with the consumption of fluctuation energy.
. In steady state the basal source is in balance with the consumption of fluctuation energy.
We are now confronted with the problem of how to distribute the basal work rate acting on the slip volume into ![]() , the fluctuation energy flux, and
, the fluctuation energy flux, and ![]() , the heat produced (Equation (18)). We are assuming that we can collapse the slip volume onto the bottom boundary.
, the heat produced (Equation (18)). We are assuming that we can collapse the slip volume onto the bottom boundary.
An empirical model governing the basal shear stress is the so-called Voellmy model (Reference Buser and FrutigerBuser and Frutiger, 1980; Reference SalmSalm, 1993) which states that the basal shear stress, T B, is governed by a dry-Coulomb friction and a ‘turbulent’ friction:

The parameter μ is the coefficient of sliding friction which is commonly defined using the internal friction angle, δ: μ = tanδ. Reference SalmSalm (1993) designated the velocity-squared friction ‘turbulent’ since it accounts for the collisional friction and random movement of the snow granules in the core of the avalanche. Although it acts in the avalanche bulk, the frictional stress is projected on the basal sliding surface.
In order to find the basal work rate we must multiply the shear, T B, by the slip velocity, u B:

The source of Salm’s turbulent friction is the fluctuation energy created in the slip volume. We therefore take
as shown in Equation (61). This procedure clarifies Salm’s well-accepted empirical approach. It identifies the source of the turbulence (the slip volume) and the region where the turbulence is destroyed (the fluidized layer). Because the translational kinetic energy of the particles is proportional to ![]() , the fluctuation energy influx depends linearly on the kinetic energy of the avalanche and is given by proportionality factor ξ, which depends on the elasticity of the snow granules and the roughness of the basal surface. Figure 5 depicts how the slip-volume model divides the basal work rate into internal energy (heat) and agitation, dependent on the slip velocity, uB. Because ξ scales the kinetic energy associated with uB, ξ is equal to p/2, where p is the density of the flow above the slip volume. In a more advanced model the parameter μ can be made a function of the fluctuation energy (Reference JenkinsJenkins, 1992).
, the fluctuation energy influx depends linearly on the kinetic energy of the avalanche and is given by proportionality factor ξ, which depends on the elasticity of the snow granules and the roughness of the basal surface. Figure 5 depicts how the slip-volume model divides the basal work rate into internal energy (heat) and agitation, dependent on the slip velocity, uB. Because ξ scales the kinetic energy associated with uB, ξ is equal to p/2, where p is the density of the flow above the slip volume. In a more advanced model the parameter μ can be made a function of the fluctuation energy (Reference JenkinsJenkins, 1992).

Fig. 5. The partition of the basal work rate, ![]() , into heat,
, into heat, ![]() , and fluctuation energy flux,
, and fluctuation energy flux, ![]() , in the slip volume.
, in the slip volume.
This description of the slip volume makes two important statements about the nature of snow avalanche flow. Firstly, there exists a single slip surface and, secondly, this slip surface is located near the basal layer. These assumptions are supported by chute and small-scale field experiments (Reference Lang and DentLang and Dent, 1983; Reference Nishimura and MaenoNishimura and Maeno, 1987; Reference Nishimura, Kosugi and NakagawaNishimura and others, 1993; Reference Dent, Burrell, Schmidt, Louge, Adams and JazbutisDent and others, 1998; Reference Kern, Tiefenbacher and McElwaineKern and others, 2004). Further evidence supporting this approach is provided by the numerical particle dynamics simulations of granular flows down inclined planes (Reference Silbert and LevineSilbert and Levine, 2002; Reference Silbert, Landry and GrestSilbert and others, 2003). These simulations show that the maximum fluctuation energy is located a few particle diameters above the rigid, inclined surface where both the translational and root-mean-square velocities are (and must be) zero. That is, there exists an interface within the flow near the running surface where the fluctuation energy is maximum.
4. Steady-State Velocity Profiles
We now apply the constitutive relations developed above to predict the internal velocity profiles observed in both steady-state chute experiments and field case studies. The momentum equation
with boundary conditions governs steady-state viscous flows in simple shear (Reference Schmid and HenningsonSchmid and Henningson, 2001). Gx is the gravitational force in the × direction, Gx = pg sin (ϕ), where g is the gravitational acceleration and ϕ is the slope angle. The solution to this equation automatically satisfies the steady-state energy equation

when the work done in the core of the avalanche by the nonconservative forces is composed entirely of the viscous shear stress. This, of course, is only true when ![]() (Equation (17)).
(Equation (17)).
The coupled system of equations governing momentum conservation (Equation (63)) and fluctuation energy conservation (Equation (41))
are to be solved for the velocity profile, u(z), and mean-square velocity, f(z). The boundary conditions for the shear stress are
and for the fluctuation energy

The boundary conditions state that no fluctuation energy escapes from the stress-free top surface. The shear stress, T(z), is given by Equation (34) and the dissipation rate, ![]() , by Equation (45).
, by Equation (45).
The coupled system of differential equations has to be solved numerically. Although general solutions can be found, we begin our investigations with a simplification that facilitates the implementation of the theory in depth-averaged models. The fluctuation energy equation (Equation (65)) can be simplified by considering only the collisional dissipation rate of ![]() :
:

Thus, we neglect the fluctuation energy source terms associated with the overburden pressure and shearing in a first step: the terms ![]() , respectively. The overburden term reduces the fluctuation energy of the granules at the bottom of the flow whereas the shearing term increases the fluctuation energy in the highly sheared fluidized layer, which is also located near the basal surface. Physically, we are assuming that the processes offset each other and the destruction of fluctuation energy is governed by the inelastic granular collisions alone (parameter α). This approach yields Equation (68) which has the analytical solution:
, respectively. The overburden term reduces the fluctuation energy of the granules at the bottom of the flow whereas the shearing term increases the fluctuation energy in the highly sheared fluidized layer, which is also located near the basal surface. Physically, we are assuming that the processes offset each other and the destruction of fluctuation energy is governed by the inelastic granular collisions alone (parameter α). This approach yields Equation (68) which has the analytical solution:
where fB is given by the boundary conditions
The steady-state velocity profile can be found directly after substitution of Equation (69) into the momentum equation (Equation (65)). The general solution is:

with
The velocity at the top surface of the avalanche, uh, is
with
where Gz is the gravitational force in the z direction, Gz = pg cos (ϕ).
The slip velocity is found by solving the shear balance equation at z = 0,
for uB:

Thus, fB, uB and uh are known. As shown in Reference Bartelt, Buser and KernBartelt and others (2005), minimizing the total energy dissipation equation (Equation (40)) provides the same solution as solving the momentum equation.
The complementary nature of the viscous and collisional processes can be identified in Equation (71), since the velocity profile is composed of a viscous and a collisional part. In the absence of fluctuations, η = 0 (no dispersive pressure, A = 0), we recover the parabolic velocity distribution of a viscous Newtonian fluid. The greater the fluctuation energy, the greater the influence of the exponential term (coefficient A). This fact is demonstrated in Figures 6 and 7 where the influence of the collisional parameters η and α is depicted. As the dispersive pressure coefficient, η, increases, the shear deformation becomes more concentrated at the basal layer and the steady-state flow velocities become larger. The dispersive pressure coefficient, η, controls the size of the fluidized layer and indirectly the mean velocity of the flow. The fluctuation velocity also increases with increasing α; that is, with increasing particle size and elasticity. The larger the value of α the larger the fluidized layer and the faster the avalanche.

Fig. 6. The influence of the collisional stress parameter, p, on the velocity profile. The larger p the faster the flow and the greater the shearing near the basal layer.

Fig. 7. The influence of the collisional dissipation parameter, α, on the velocity profile. (a) The larger α the faster the flow; (b) the larger α the larger the fluidized layer height and fluctuation velocities.
The proposed constitutive theory requires six constitutive parameters (μ,ξ,v,η,k,α) to model steady-state velocity profiles. These can be determined from experiments performed on the Swiss snow chute (Reference Kern, Tiefenbacher and McElwaineKern and others, 2004). Direct measurement of the shear and normal stresses by basal force plates (Reference Platzer, Bartelt and JaedickePlatzer and others, in press) provides the Coulomb friction parameter, μ. In accordance with the experimental results for wet snow avalanches we take μ = 0.4, in agreement with the measurements of Reference Lang and DentLang and Dent (1983). Optical velocity sensors installed at the basal running surface of the chute are used to determine the second parameter, ξ. Since the basal slip velocity, uB, is measured as a function of the flow height, h, and normal stress, Gz, the value of ξ can be determined directly from Equation (76). Typical slip velocities are of order uB ≈ 2–4m s–1, providing ξ values between 10 and 40 kg m–3. The velocity sensors are placed at different height locations on the chute sides as well as on a specially designed flow wedge located in the middle of the chute. These sensor arrays provide the velocity profile and the remaining four constitutive parameters. The shear viscosity, u, is uniquely determined since it governs the shear deformations in the plug flow, i.e. the slope of the velocity profile in the upper regions of the flow. We found values ranging between 30 and 70kgm–1s–1. Because this value represents the viscosity of the plug region of the avalanche core, it is higher than the ‘fluidized’ viscosity values found by Reference Nishimura and MaenoNishimura and Maeno (1987). The dispersive pressure coefficient, η, and fluctuation energy diffusion coefficient, K, determine the size of the fluidized layer (the region of large shear gradients) and subsequently the overall mean velocity of the flow. Since the shear layer is small, the mean velocity is essentially the plug velocity. Hence unique values for q and K can be found. The final parameter, α, which governs the collisional dissipation, is found by direct application of Equation (46). For the snow flows considered in the following with coefficients of restitution of e ≈ 0.5 and particle sizes 0.005 < d < 0.5m, we have 0.001 < a < 0.1 m. The longitudinal viscosity (λ) is not required in our steady-state analysis.
Figure 8 presents two constitutive parameter combinations that fit the experimental velocity profile measurements made in chute experiments with wet snow by Reference Kern, Tiefenbacher and McElwaineKern and others (2004). Figure 9 fits the experimental velocity profile measurements made with ground radar by Reference GublerGubler (1987) at the Aulta (Switzerland) avalanche track. Note that the value of the constitutive parameters does not change significantly between the chute experiments and the field experiment. Both Reference Dent and LangDent and Lang (1983) and Reference Norem, Irgens and SchieldropNorem and others (1987) had to introduce a yield stress in their constitutive formulations in order to model the measured velocity profiles, which also contain a ‘plug’ region. Because we employ a collisional stress which is a function of the fluctuation velocity and not the shear gradient, we no longer need an empirical stress cut-off.

Fig. 8. Comparison between the measured velocity profile of a snow-chute avalanche (Reference Kern, Tiefenbacher and McElwaineKern and others, 2004) and proposed theory. The fluctuation velocities are of the same order as the translational velocity. Constitutive parameters (a) α = 0.02 m; K = 0.05 kg m–1 s–1; η = 300 kg m–1; μ = 0.40; ξ = 35kgm–3; v = 70kgm–1s–1. (b) α = 0.01m; K = 0.05 kg m–1 s–1; η = 120 kg m–1; μ = 0.40; ξ = 10kgm–3; v = 30kgm–1s–1. Flow height of the avalanche h = 0.5 m; density p = 300 kg m–3.

Fig. 9. Comparison between the measured velocity profile of a small field avalanche (Reference GublerGubler, 1987) and proposed theory. The fluctuation velocities are slightly smaller than the translational velocity. Different parameter combinations can match the observed results. Parameter combination (a) predicts a large fluidized layer; parameter combination (b) a smaller fluidized layer. Constitutive parameters: (a) α = 0.03 m; K = 0.05 kg m–1 s–1; ξ = 190 kg m–1; μ = 0.40; ξ = 35kgm–3; v = 30kgm–1s–1. (b) α = 0.01m; K = 0.05 kgm–1 s–1; ξ = 120kgm–1; α = 0.40; ξ = 5.0kgm–3; v = 10 kg m–1 s–1. Flow height of the avalanche h = 1.0 m; density p = 300 kg m–3.
Although the fluidized layer is thin, it will have a dramatic influence on the overall sliding because the shear resistance can be significantly reduced in this region. Our constitutive model predicts that long avalanche run-out distances are possible if there is a continual supply of fluctuation energy from the basal surface. The snow type (wet, dry, granule size) will govern the overall flow behaviour, since the consumption and diffusion of fluctuation energy in the core of the avalanche depends on these properties.
The above results are based on the simplified solution of Equation (65). A comparison between the numerical solution of the full coupled system and the simplified analytical solution of the uncoupled solution is shown in Figure 10 for the Aulta avalanche example. We find good qualitative agreement between the numerical and analytical solutions, although the numerical solution predicts higher plug flow velocities. This implies that the creation of fluctuation energy from shearing is slightly greater than the destruction of fluctuation energy from the overburden pressure.

Fig. 10. Comparison between the numerical solution when the collisional dissipation rate, ![]() is given by Equation (45) and the analytical solution when
is given by Equation (45) and the analytical solution when ![]() is given by Equation (68). The numerical and approximate solutions have the same form; the numerical solution predicts slightly higher plug velocities.
is given by Equation (68). The numerical and approximate solutions have the same form; the numerical solution predicts slightly higher plug velocities.
5. Conclusions and Outlook
The proposed fluctuation–dissipation relations provide a framework for developing more accurate constitutive theories for depth-averaged avalanche-dynamics models. They reveal that the interaction between the avalanche with the basal surface and energy dissipation by macro-viscous and micro-collisional processes are interrelated by simple thermodynamic constraints. These constraints are governed by the mechanical work rate and injection of fluctuation energy at the basal layer of the avalanche. Further progress is dependent on measurement of these processes in chute experiments or from numerical simulations (see Reference LougeLouge, 1994). Our future experimental work will concentrate on identifying the dimension of the basal slip volume and resolving the problem of how to partition the basal work rate into the generation of fluctuation energy and heat as a function of the surface roughness and snow properties. It should therefore be possible to improve existing avalanche-dynamics models which presently rely on empirical models that require extensive calibration to fit flow velocities and run-out distances (Reference Buser and FrutigerBuser and Frutiger, 1980; Reference Bartelt, Salm and GruberBartelt and others, 1999; Reference Sovilla, Burlando and BarteltSovilla and others, 2006).
Our constitutive proposal is a first attempt to apply fluctuation–dissipation relations to geophysical flows that are governed by the interaction with the basal surface. The model can already explain the observed velocity profiles of snow avalanches without using some z-dependent viscosity in the avalanche core. In the proposed model the viscosity coefficient is a material constant and the z-dependent viscous shearing is determined by the random motion of the snow granules. We can therefore model the whole velocity profile without using some macro-viscous rheology which empirically divides the avalanche core into a bulk and a highly sheared part (Reference Dent and LangDent and Lang, 1983; Reference Nishimura and MaenoNishimura and Maeno, 1987; Reference Norem, Irgens and SchieldropNorem and others, 1987; Reference SalmSalm 1993). Because the fluctuation energy diminishes with increasing height, the velocity gradient becomes so small that the upper region of the flow behaves like a rigid plug. The size of the viscous shear layer is given by fluctuation energy input as well as the snow properties, specifically the fluctuation energy transport and collisional damping properties. Hence the model explains both wet and dry dense snow avalanche flow regimes. Finally, it predicts that avalanches can reach long run-out distances when the viscous shear resistance of the flowing snow is reduced by a continual supply of fluctuation energy at the basal surface.
The interaction of the viscous and collisional processes introduces an important thermodynamic constraint on the constitutive formulation. The product of the viscous strain rate and fluctuation energy must describe a single energy dissipation process. This fact illustrates the complementary character of the viscous and granular descriptions of snow avalanches. Accordingly, their interaction is required to be reciprocal. By finding the associated quadratic form of the total dissipation, we can identify the symmetric crossproduct coefficients of the dissipation matrix. The variables of the quadratic form define the viscous and collisional processes uniquely. Since the diagonal coefficients of the dissipation matrix are constant, the constitutive formulation defines a linear dissipative system. Interestingly, such systems are governed by dissipation functionals that obey general variational principles such as the principle of minimum entropy production ![]() (Reference Leopold and LangbeinLeopold and Langbein, 1962; Reference Glansdorf and PrigogineGlansdorf and Prigogine, 1974; Reference Bartelt, Buser and KernBartelt and others, 2005). A variational principle provides us with a powerful tool to investigate our complex flow systems, including their stability with regard to external disturbances. It implies that dense snow avalanche flows are near to equilibrium, that is, they tend to steady state under the given basal boundary conditions – a result that can be corroborated with further field studies to quantify the relationship between fluctuation energy and the basal work rate.
(Reference Leopold and LangbeinLeopold and Langbein, 1962; Reference Glansdorf and PrigogineGlansdorf and Prigogine, 1974; Reference Bartelt, Buser and KernBartelt and others, 2005). A variational principle provides us with a powerful tool to investigate our complex flow systems, including their stability with regard to external disturbances. It implies that dense snow avalanche flows are near to equilibrium, that is, they tend to steady state under the given basal boundary conditions – a result that can be corroborated with further field studies to quantify the relationship between fluctuation energy and the basal work rate.
















