No CrossRef data available.
Published online by Cambridge University Press: 30 January 2017
The dipole moment μ of an H2O molecule in the orientationally disordered ices is greater than the moment of an isolated molecule, 1.84 D, due to two factors: (i) the mutual polarization of molecules, and (ii) the short-range average correlation of the dipole vectors, if the molecules are able to reorient. The magnitude of the average enhancement is given by Kirkwood's equation,
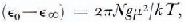 1
1
where ϵ0 and ϵ∞ are respectively the limiting low- and high-frequency relative permittivity of orientational polarization, N is the number density of dipoles, k is the Boltzmann constant and T is the temperature. The dipolar correlation factor g is defined by,
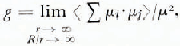 2
2
where μi and μj are the dipole moments of molecules i and j in a spherical region of radius r immersed in a larger spherical region of radius R and the angular brackets indicate average over all molecules i and all their orientations. In view of the defects, vacancies, imperfections, etc., in ice, it is not certain if the limits in Equation (2) have any experimental significance. However, an approximate value of g can be calculated by taking molecules up to the second co-ordination shell.
The theoretical value of g for polycrystalline ice VI which is fully disordered (within the restrictions of ice rules) has been calculated by taking molecules up to the second nearest neighbours, in both the dendritic and non-dendritic models. The calculations were done for two kinds of molecules, I and II, having multiplicities 2 and 8 respectively, in the tetragonal unit cell in space group P42/nmc, and, through the use of symmetry, keeping to a minimum the number of scalar products.
In both the dendritic and non-dendritic, models, gI is 10%, or more, greater than gII and the appropriately weighted values of g are 2.342 in the former and 2.065 in the latter model. The effect of ring closure is, therefore, to reduce the value of g by 13%. The limiting high temperature experimental value of g from Equation (1), using Onsager's theory for the enhancement of the dipole moment by its own reaction field, is 2.42 (Johari and Whalley, 1976). By analogy with the 10% discrepancy between the theoretical and experimental values of g of ice I, a better estimate of the experimental g of ice VI (using a reaction field other than that given by the Onsager theory) would be about 10% less than this value. Thus the suggested experimental g of ice VI (2.18) is close to the theoretical values obtained from either of the two models and there is little contribution to g from neighbours beyond the second co-ordination shell.