1. INTRODUCTION
Following early work that established the ability to measure ice motion and topography using interferometric synthetic aperture radar (InSAR) (Goldstein and others, Reference Goldstein, Engelhardt, Kamb and Frolich1993; Joughin and others, Reference Joughin, Winebrenner and Fahnestock1995; Rignot and others, Reference Rignot, Jezek and Sohn1995), spaceborne radars have been used extensively to study glaciers and ice sheets (see five pages of references in Joughin and others, Reference Joughin, Smith and Abdalati2011a). Complementing conventional InSAR, speckle tracking has developed in parallel as an important means for measuring ice flow velocity (Gray and others, Reference Gray1998; Michel and Rignot, Reference Michel and Rignot1999). This latter method makes use of partial correlation (coherence) between pairs of SAR images acquired from similar positions (within a few hundred meters) at different times, where the surface remains relatively unchanged between passes. If the correlation is adequate, the displacement of the radar speckle pattern can be tracked from one image to the next, even in the most otherwise featureless areas of an ice sheet. Speckle tracking and InSAR have evolved to the point where several ice-sheet scale maps of velocity have been produced (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010a; Rignot and others, Reference Rignot, Mouginot and Scheuchl2011; Moon and others, Reference Moon, Joughin, Smith and Howat2012; Rignot and Mouginot, Reference Rignot and Mouginot2012).
Although major progress has been made measuring ice flow velocity in Greenland (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010a; Moon and others, Reference Moon, Joughin, Smith and Howat2012; Rignot and Mouginot, Reference Rignot and Mouginot2012; Nagler and others, Reference Nagler, Rott, Hetzenecker, Wuite and Potin2015; Rosenau and others, Reference Rosenau, Scheinert and Dietrich2015; Mouginot and others, Reference Mouginot, Rignot, Scheuchl and Millan2017), the quality of the earlier products has been limited by a number of factors. While sensors such as ALOS-PALSAR, RADARSAT and TerraSAR-X have collected data over Greenland, none have individually collected sufficient coverage to map velocity for the entire ice sheet with sufficient accuracy. The gaps in their coverage are due largely to the fact that these instruments and their corresponding acquisition plans were not optimized for ice-sheet mapping. For example, C-band images decorrelate quickly in the high-accumulation areas of southeast Greenland, so they yield limited amounts of useable data when imaged with the 24-day repeat cycle of RADARSAT. While ALOS-PALSAR, operating at L band, generally produced coherent image pairs in high accumulation areas, the results are often corrupted by ionospheric distortion, producing errors of up to many tens of meters per annum. For coastal areas, such errors are less consequential because they tend to be small relative to glacier speeds (100s to 1000s of meters per annum), making such data extremely useful for studying outlet glacier behavior (Joughin and others, Reference Joughin, Abdalati and Fahnestock2004; Rignot and Kanagaratnam, Reference Rignot and Kanagaratnam2006; Moon and others, Reference Moon, Joughin, Smith and Howat2012, Reference Moon2014). The majority of an ice sheet's area, however, flows at speeds of <100 m a−1 so that errors exceeding 10 m a−1 make these data much less useful to many studies. Incomplete maps are also a limitation for several applications, particularly for initializing ice-sheet models (Perego and others, Reference Perego, Price and Stadler2014).
Speeds in the middle of the ice sheet generally tend to evolve slowly over decades, allowing temporal resolution to be sacrificed to improve coverage and accuracy. Here we describe the creation of a full ice-sheet velocity map produced by averaging data collected over 20 years and processed as part of the Greenland Ice Sheet Mapping Project (GIMP). We have supplemented these radar data with feature-tracked results from Landsat 8 (Jeong and Howat, Reference Jeong and Howat2015; Fahnestock and others, Reference Fahnestock2016). For a number of reasons described below, this multi-sensor map is more accurate (errors approaching 1–2 m a−1 for much of the slow-moving interior) than previous results. Although more rapidly changing coastal velocities are averaged in this map, for some studies it may be an advantage to have velocity averaged over more than a decade rather than a brief snapshot of a seasonally- to annually-varying signal.
2. METHODS
We processed a large volume of SAR data using methods previously described (Joughin, Reference Joughin2002) with additional refinements as described below. Similar to other projects (Mouginot and others, Reference Mouginot, Rignot, Scheuchl and Millan2017), we have adapted our velocity mosaicking tool to also incorporate velocities derived from Landsat 8 optical data.
2.1. Speckle tracking
We applied basic cross-correlation techniques to track the displacement of the speckle patterns in pairs of SAR images (Gray and others, Reference Gray1998; Joughin, Reference Joughin2002). This technique works well when coherence is preserved, which requires that the relative positions of scatterers in a resolution element do not change much on the scale of a wavelength (3.1 cm at X-band to 23.6 cm at L-band). If the relative motion of scatterers is small, then the cross-correlation function for two images has a sharp peak that allows displacement to be resolved to sub-pixel (<1/10 of a pixel) accuracy. Since the radar signal penetrates many meters in dry snow (Rignot and others, Reference Rignot, Echelmeyer and Krabill2001), the change in scatterer positions as firn compacts can cause temporal decorrelation. Thus, it is often difficult to achieve satisfactory results in high accumulation areas where firn compaction rates are greater. Because this effect is wavelength dependent, longer wavelength instruments (e.g., L-band) work better in areas of high snowfall. In addition to temporal decorrelation, volume scattering from firn can also cause a large non-temporal reduction in correlation (Hoen and Zebker, Reference Hoen and Zebker2000). Thus, especially in high accumulation regions, there are many instances where a SAR collects data, but velocity information cannot be obtained (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010a).
To produce velocity estimates from speckle tracking, we first cross-correlate pairs of images to obtain the relative shifts in locations from the first to the second image (i.e., the offsets that maximize cross correlation). Following this cross-correlation procedure, the data are automatically culled to remove outliers and then smoothed to further reduce noise, typically to a resolution of ~0.5 km (Joughin, Reference Joughin2002). In addition, we use visual inspection to manually screen each set of offsets to remove low quality data. For example, longer-wavelength images are more susceptible to ionospheric distortion caused by auroral activity (Gray and others, Reference Gray, Mattar and Sofko2000). In these instances, subtle phase gradients caused by the ionosphere introduce artifacts in SAR processing such that the radar-along track coordinates are displaced by several meters. These errors take the form of ‘streaks’ that extend across the entire image, roughly perpendicular to the satellite track. At X-band (3.1 cm) such errors are rarely discernable, but in some instances at L-band the errors can exceed 100 m a−1. The level of ionospheric errors can be spatially variable so that a speckle-tracked pair may have some areas with severe distortion and other areas that are nearly error-free. We manually removed many of the worst of these artifacts, which typically have dimensions of a few kilometers in the along-track direction and extend across the entire width of the image.
The raw, culled offsets are sensitive to the ice motion and the elevation of the ice-sheet surface. The sensitivity to topography is determined by the interferometric baseline, which is the separation between the satellite's orbital paths on the successive image acquisitions. In general, knowledge of the satellite's orbit is not sufficiently well known to allow us to calculate velocities accurately, so we must solve for the baseline parameters. Because the offsets measure only relative displacement, we also must solve for a gross offset to make the estimate absolute. The baseline and gross offset are represented as a 4- (linear variation in two components) or 6-parameter (quadratic) function. To determine the baseline parameters, we use a least squares fit to points of known elevation and velocity (see description of the control points below) (Joughin and others, Reference Joughin, Kwok and Fahnestock1996a, Reference Joughin, Winebrenner, Fahnestock, Kwok and Krabillb). A similar fitting procedure is used to calibrate the azimuth offsets. Once the baseline is known, a DEM is used to compute and remove the effect of topography from the offset data. After this correction, the offset data provide an absolute estimate of ice displacement.
The image offsets are computed in radar coordinates. The horizontal along-track coordinate parallels the direction of the satellite orbit, similar to the case for optical sensors. The radar slant-range-coordinate, however, is directed in the radar line-of-sight, which is typically at an incidence angle of 20°–45° from vertical. As a result, the slant-range offsets are sensitive to both horizontal and vertical motion. For ice flow, the vertical motion generally is due to a combination of displacement as ice flows up and down over bumps (surface-parallel flow) and a surface mass balance (SMB) dependent submergence/emergence velocity (Cuffey and Paterson, Reference Cuffey and Paterson2010). Following earlier work, we make the assumption that submergence/emergence term is negligible, and thus, assume that all vertical displacement is due to surface-parallel flow (Joughin and others, Reference Joughin, Kwok and Fahnestock1996a; Joughin, Reference Joughin2002). Some of the error introduced by neglecting the submergence/emergence velocity is compensated for as a side-effect of the baseline fitting procedure, which compensates for additional errors that can be represented by the baseline parameterization (e.g., a regional mean or gradient in the accumulation). Further uncertainty related to this assumption is discussed below. Applying the surface-parallel flow assumption, we estimate and remove the vertical displacement to compute the component of horizontal velocity orthogonal to the radar's orbital path (Joughin and others, Reference Joughin, Kwok and Fahnestock1996a). Finally, we rotate the results from radar ground-range coordinates to the output-grid coordinates as part of the mosaicking procedure described below (Joughin, Reference Joughin2002).
We estimate several sources of error in our results. First we use the statistics in the neighborhood around each offset to assess the local error from the matching procedure (Joughin, Reference Joughin2002). This method performs well in regions with low strain rates, but can bias error estimates high where local variability is due to motion rather than noise (e.g., along a shear margin). This method also does not detect longer-wavelength errors such as those arising from ionospheric ‘streaks’. For each dataset, we assessed the average level of ionospheric error for all of the tracks, which was added in quadrature as an additional error term to the azimuth-offset data. Except for a few cases where the errors were particularly large, the same error was assumed for an entire set of data (e.g., all RADARSAT scenes from 2006). As a result, for a given scene the errors could be substantially under- or over-stated. To some extent, such fluctuations are evened out by averaging data from numerous sources to achieve the final estimate. To account for errors in the baseline fitting procedure, we use the covariance from the least-squares parameter fits to derive an error estimate (Joughin and others, Reference Joughin, Kwok and Fahnestock1996a). Finally, errors are also introduced through the DEM used to transform the line-of-sight displacement to ground-range coordinates under the surface parallel flow assumption. Lacking a good model for the slope errors in the GIMP DEM (Howat and others, Reference Howat, Negrete and Smith2014), we assume this speed-dependent error equals 3% of the ground-range component of the velocity vector. Analysis of GPS data suggests that this is a reasonable assumption (Ahlstrøm and others, Reference Ahlstrøm2013).
2.2. Crossing orbit phase
The phase difference between two coherent InSAR images is sensitive to topography and ice motion directed along the radar line of sight (Goldstein and others, Reference Goldstein, Engelhardt, Kamb and Frolich1993). This phase difference essentially conveys the same information as the speckle-tracked range component of the offsets, but with much better resolution (10s rather 100s of meters) and accuracy (centimeters rather than decimeters). Unlike speckle-tracked data, which resolves motion in two directions, phase information from an InSAR pair collected along a single satellite repeat track provides only the line-of-sight (range) component of the displacement vector. It takes InSAR observations from three unique directions to resolve the full 3-D displacement vector, but such acquisitions are rarely available. If we assume the flow is surface-parallel, then the velocity vector lies in the plane locally tangent to the surface, which reduces the problem from three to two dimensions. Applying this assumption, we produce horizontal velocity estimates using line-of-sight phase estimates from crossing ascending and descending orbits (Joughin and others, Reference Joughin, Kwok and Fahnestock1998).
As with speckle tracking, we estimate the baseline using control points. We then use the baseline estimate and a DEM (Howat and others, Reference Howat, Negrete and Smith2014) to remove the effect of topography. This DEM also is used to estimate the parameters of the plane tangent to each point on the surface as required for the surface-parallel flow approximation. Once the procedures just described have been applied, a linear combination of the phases from crossing ascending and descending orbits provides an estimate of the horizontal velocity vector (Joughin and others, Reference Joughin, Kwok and Fahnestock1998).
The phase error due to random noise for the smoothed phase is determined in part by the level of correlation between images (Joughin and others, Reference Joughin, Winebrenner and Percival1994), but such errors in most cases are small relative to other sources of error such as the troposphere and ionosphere (Rosen and others, Reference Rosen2000). Since we do not have a good way to estimate these errors on a scene-by-scene basis, we assume a fixed error of pi radians (~0.75 cm at X-band to 6 cm at L-band). The assumed error's frequency dependence is appropriate in an ad hoc way for ice sheets where dispersive ionospheric errors tend to be larger than tropospheric errors. Unfortunately, we do not have a more rigorous way to assess phase errors, and the values used represent a best guess at actual levels. The final error estimate combines this phase error in root-sum-square fashion with the error from the baseline parameter fit (Joughin and others, Reference Joughin, Kwok and Fahnestock1996a). These errors in radar geometry are then propagated to compute errors in the final geometry of the map projection. Because of the track orientation, errors in the north-south direction are generally about a factor of three larger than those in the east-west direction. As for the speckle-tracked estimates, we assume a DEM-dependent error equal to 3% of each horizontal velocity component.
2.3. Optical feature tracking
We also compute velocities by applying a simple cross-correlation procedure to high-pass filtered optical (Band 8 from Landsat 8) data, using algorithms that are similar to those used by other groups (Ahn and Howat, Reference Ahn and Howat2011; Rosenau and others, Reference Rosenau, Scheinert and Dietrich2015; Fahnestock and others, Reference Fahnestock2016; Mouginot and others, Reference Mouginot, Rignot, Scheuchl and Millan2017). Unlike the SAR data, the Landsat images are reprojected to the output coordinate system prior to matching. As a result, the matching procedure ideally should provide absolute displacements directly from the offsets once a correction for scale distortion due to the coordinate system of the projection has been applied. In practice, however, the uncertainties in the image registration are too large to produce sufficiently accurate results. Thus, we use a least-squares procedure to fit a plane to each scalar offset field, using the control points described below. After applying these corrections, the offsets only need to be scaled by the time interval between images to produce an estimate of the velocity.
For the Landsat 8 data we use a similar procedure as that for the SAR data to estimate the matching error from neighborhood statistics. When we examined the data more closely, however, we found there were longer wavelength errors of comparable or greater magnitude than those detected by the neighborhood statistics, which are likely related to sensor errors or atmospheric effects. Since we use the radar data as control points (see below), we have a well sampled set of control points that generally sample the full scene. We assume that the control points (averaged from multiple data as described below) are for more accurate than the results for single Landsat pair. As a result, the residual errors from the parameter fits provide an approximate estimate for the average error for the full scene averaged over all length scales but with no detail on the spatial variability. On the other hand, while the neighborhood statistics do not estimate all sources of error, they do at least provide information on the spatial distribution of the errors related to the matching procedure. Thus, we used the following procedure to combine these error estimates: First, we computed the scene-wide average variance from the neighborhood statistics and subtracted this value from the variance for residual error from the parameter fit. This difference provides a scene-wide estimate of the longer-wavelength errors. Then at each point, we added this long wavelength error to the spatially varying neighborhood statistics. The average variance of this result is identical to the scene-wide residual, but it conveys more information about the spatial variability of the error. Finally, we added to this error the uncertainty associated with the fitted parameters, which is derived from the covariance matrix produced by the least-squares fitting procedure.
2.4. Control points
All of the methods described above require calibration with control points of known elevation and velocity. We used several sources of such data, which are shown in Figure 1. Exposed bedrock at the periphery of the ice sheet where the velocity is effectively zero (white circles, Fig. 1) provides a major source of control points. We extracted the elevation at these points from the GIMP DEM (Howat and others, Reference Howat, Negrete and Smith2014). Especially when solving for parameters on tracks that extend well inland, the coastal bedrock points cannot fully constrain the solution, and points are needed on the ice sheet. One important inland source of control data comes from GPS measurements at 30 km intervals, nominally along the ice sheet's 2000 m contour (Thomas and others, Reference Thomas2000; large red and light blue circles in Fig. 1). At this elevation, changes in velocity since the measurements were made generally should be small (see discussion on GPS control points), allowing us to use these data as a source of control. We did, however, remove points immediately upstream of Jakobshavn Isbrae, where significant changes in speed are likely to have occurred (Joughin and others, Reference Joughin2012). Along the slow-moving ice divides, we used balance velocities where the speeds are <5 m a−1 (small red and dark blue circles Fig. 1) (Bamber and others, Reference Bamber, Hardy and Joughin2002). While these velocities may have large errors in a relative sense, because we have limited their use to slow-moving regions the errors are small in an absolute sense. It is important to note that each solution to determine a baseline typically involves fitting for 2–6 parameters using tens to hundreds of control points. Thus, in most cases the solution should not be adversely affected by a few bad points.

Fig. 1. Locations of the GPS, balance (V b) and rock (V r) control points used to calibrate the offsets and interferograms included in the velocity mosaics plotted over the complete velocity mosaic (color background). Points are color-coded by type as shown in the legend and described in the text.
In some cases, the distribution of control points is insufficient to adequately constrain the solution for the baseline (e.g., if all the points are clustered so they cover only a small part of the image area). In such cases, we ‘bootstrapped’ additional control points. Specifically, we computed velocities from nearby satellite tracks that were well controlled by the standard control points and used these estimates to fit for the parameters of the less well-constrained tracks. These extra points are not shown in Figure 1, nor are they used in evaluation of the results.
The phase data represent a special case, because we could not rely on bedrock control points. In general, the flow speed is non-zero at the margin, creating a discontinuity between the rock and the ice. In many cases, this discontinuity produces a phase jump of more than one interferometric fringe, making unwrapping (removing the across 2π phase ambiguity) across the discontinuity inaccurate. Thus, we have masked out all phase on exposed rock. In the absence of the rock (coastal) control points, we generated a set of control points using the speckle-tracked data averaged across all years for regions of the ice sheet moving <100 m a−1, which we combined with the GPS and balance-velocity points.
As with the phase data, for the Landsat 8 offsets, we used other data to produce a set of control points for all slow moving (<100 m a−1) areas of the ice sheet. In this case, we combined the phase and speckle-tracked data to generate a densely sampled (every few km) set of control points, which were combined with the rock, GPS, and balance-velocity control points (Fig. 1). This combined set of points was used for the least squares fits applied to the Landsat 8 data as described above. If we were interested in short-term variation, this approach would not have been appropriate, but it worked well in the context of producing a product that represents a decadal-scale average.
2.5. Mosaicking
The final velocity mosaics are produced with our mosaicking software, which produces the various types of velocity estimates and combines them to produce a single result (Joughin, Reference Joughin2002). For Greenland the final products produced by the mosaicking code are horizontal velocities and associated errors in polar stereographic coordinates with a standard latitude of 70° and a central meridian of −45° (AKA EPSG:3413 or NSIDC Sea Ice Polar Stereographic North).
To produce the mosaics, the program cycles through each individual dataset (e.g., offset pair) or group of data (phases from crossing orbits) to produce an intermediate velocity and error estimate in the output coordinates, which it saves in a temporary buffer. In addition to the algorithms described above, the software can also produce hybrid phase-offset estimates whereby the range offsets are replaced by the interferometric phase and combined with the azimuth offsets. Each of these intermediate results is weighted by the inverse of its estimated error to produce an error-weighted average. Additional weights are applied near the edges as part of a ‘feathering’ operation that helps avoid discontinuities at seams. Joughin (Reference Joughin2002) provides further detail on how the data are combined.
Our mosaicking processor produces a map of the formal error estimate assembled from the various individual error estimates as described above. Some sources of error are well characterized and others far less so. Further assessment of the fidelity of the errors is given below. It is important to remember that these are formal errors, which means they are estimates of uncertainty, which themselves have some not particularly well quantified level of uncertainty. Furthermore, although the errors are provided as standard deviations with an implicit assumption that the errors are Gaussian, the actual probability distributions of the errors likely have heavier tails. For example, it is not uncommon for a field of speckle-tracked offsets to have a few spurious matches more than five times the standard deviation for the population as a whole. Most of these points are removed in our culling procedures, but extreme outliers occasionally may slip through. As a consequence, the errors for this map should be treated as a measure of approximate or relative quality. Care should be taken when using these estimates to conclude some feature of the data is statistically significant.
The 3% error related to the slope correction in the surface-parallel assumption is common to images with the same geometry, so it is not reduced by averaging. Moreover, for a given velocity, the level of error is the same for all source products and is not indicative of the relative quality of the data. Thus, we do not include it in error-weighted averaging used to produce the mosaic. As a consequence, this error is not included in our final error estimates, which maintains consistency with our time series products (not described here). For users of the data this error is trivial to compute and add in quadrature to the mosaicked error estimate to determine the total error.
3. RESULTS
Table 1 lists the sensors used to collect the data used in our mosaic, along with corresponding acquisition periods. Although our mosaicking software normally produces a single output combining all data, we have also produced individual mosaics to help illustrate the quality of each data type. These intermediate products are meant to be illustrative and are not included as part of our standard distribution. The remainder of this section describes these individual mosaics as well as the final mosaicked velocity map.
Table 1. Sensors and periods of acquisitions for the image data used in the velocity mosaic
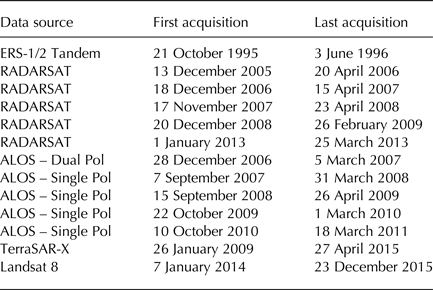
Although some Landsat 8 data in southern Greenland was acquired near the Winter Solstice, the majority of the data were collected from March to October in 2014 and 2015.
3.1. Speckle tracked data
Figure 2a shows a mosaic of the velocity results from speckle tracking using the radar data listed in Table 1. Since available ERS data are largely from the 1-day phase campaign, they are not included in speckle-tracked results. For each of the six annual RADARSAT campaigns, there were typically 3–4 image pairs available at each point. Thus, in regions of high correlation the mosaic may include an average of up to ~24 RADARSAT speckle tracking estimates, particularly in the north, where the images tended to remain coherent and the radar swaths overlap substantially. By contrast, for much of the southeast, there were no useable RADARSAT data due to poor correlation except for some outlet glaciers where there were features that could be tracked (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010a).

Fig. 2. Ice-sheet velocity estimates plot from (a) speckle tracking (b) interferometric phase in interior regions where phase can be unwrapped, and (c) Landsat 8. Speeds are displayed as color over a gray-scale SAR mosaic (Joughin and others, Reference Joughin, Smith, Howat, Moon and Scambos2016a).
The full ALOS dataset provides ~1–3 pairs at each location, although there were a few locations for which there were no pairs. For most of the ALOS pairs the coherence was sufficient to obtain matches. Many of the ALOS offsets, however, were corrupted by strong azimuth streaking from the ionosphere. Thus, after editing, many of these results had large gaps, particularly in the south.
When combined, the results from speckle-tracking yield a nearly complete mosaic (Fig. 2a). A variety of SAR data and correlation window sizes were used to produce this mosaic. Moreover, individual offsets estimates underwent some spatial smoothing to reduce errors. Thus, the resolution of the combined product varies spatially because of the variable mix of data at each point, but it is generally in the range of ~300–700 m (nominally 500 m). Visual inspection reveals some residual streaking artifacts visible in the slower moving regions, particularly along the divide in the south. To more quantitatively examine the quality of these data, Table 2 includes the means, μ
x
and μ
y
, and standard deviations, σ
x
and σ
y
, for the differences between the velocity estimates and the control point data. These statistics provide only proxies for the actual errors because the control points themselves have some degree of uncertainty. In addition, Table 2 also includes the corresponding error estimates,
![]() $\hat \sigma _x $
and
$\hat \sigma _x $
and
![]() $\hat \sigma _y $
, produced by the mosaicking software.
$\hat \sigma _y $
, produced by the mosaicking software.
Table 2. Mean (μ x , μ y ) and standard deviations (σ x , σ y ) of differences between x- and y-components of the velocity estimates and control points shown in Figure 1
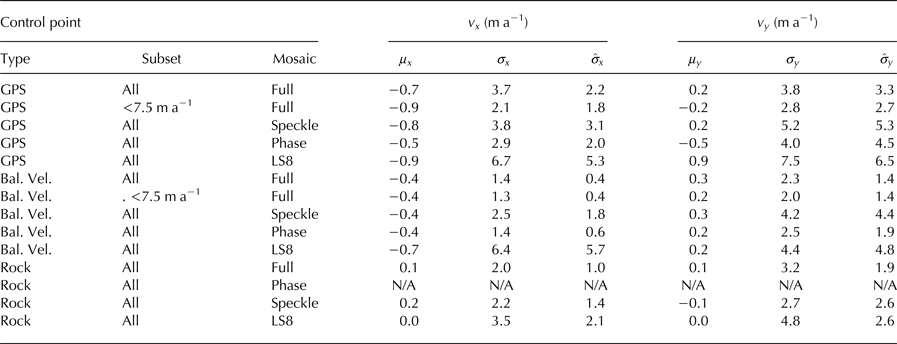
Also included are the formal error estimates
![]() $(\hat \sigma _x, \hat \sigma _y )$
for the corresponding sets of points.
$(\hat \sigma _x, \hat \sigma _y )$
for the corresponding sets of points.
Comparison of the speckle tracked results with the GPS data yields differences with standard deviations of 3.8 and 5.2 m a−1 for the x and y components, respectively. While these numbers agree well with the corresponding formal error estimates (3.1 and 5.3 m a−1), at least some of the difference likely is attributable to small (a few m a−1) changes at some of the GPS points. For the rock and slow-moving balance-velocity regions, the differences range from 2.2 to 4.2 a−1, which generally agree with the formal errors to within 1 m a−1 or better. Some of the errors may be due to variations in the quality of the control points, so in all three cases the formal errors agree reasonably well with the differences, suggesting they provide a reasonable estimate of the errors at least in an average sense.
It is important to note in considering these and subsequent comparisons that control points were used to constrain the baseline fits, which should reduce the differences between the control points and the data. This effect, however, should be minor since the number of control points (~50–1000) relative to the number of degrees of freedom for each fit (≤6) is large. In these comparisons, errors could be larger in regions not well constrained by control points. We have made every effort to avoid such errors (see discussion on bootstrapping control points). To the extent that such uncertainty exists, it is included in our error model through our estimates for uncertainty in the baseline estimate.
3.2. Crossing orbit phase data
Figure 2b shows the velocity derived from crossing-orbit phase data, which is limited to the slower-moving regions on the ice sheet. In most areas ~1–6 descending RADARSAT interferograms were combined with 1–3 ascending ALOS interferograms to produce surface-parallel-flow approximated velocity estimates. With the long time intervals between repeat images (24 days or more), the phase could not be unwrapped for much of the fast-flowing area. As a result, the map only includes speeds up to ~100 m a−1. In the southeast where RADARSAT pairs did not correlate well, we combined descending-orbit 1-day phase data from ERS-1/2 tandem pairs with the ascending-orbit ALOS data. In the mosaicking process, each descending image was combined with each ascending image. As a result, each interferogram may have contributed to multiple estimates that were subsequently averaged (i.e., individual estimates were not necessarily independent), which could cause error estimates to be biased low. Since the number of ascending pairs was small (~≤3), any bias should have been small (~≤1
![]() $(\sim\!\!{\rm \leqslant} {\rm 1}/\sqrt 3 )$
. Moreover, since we used an ad hoc estimate for the phase error, we may have partially compensated for this effect in our selection of the nominal phase error.
$(\sim\!\!{\rm \leqslant} {\rm 1}/\sqrt 3 )$
. Moreover, since we used an ad hoc estimate for the phase error, we may have partially compensated for this effect in our selection of the nominal phase error.
Comparison of the results in Figure 2, indicates that the phase-only result is smoother and less noisy than the speckle-tracked results. The differences with the GPS control points (Table 2) are σ x = 2.9 and σ y =4.0 m a−1, which may include some degree of actual change for a few drainage basins. As with the speckle-tracked data, these values agree well with the formal error estimates. Table 2 also indicates that the phase data agree well with balance-velocity points (σ x = 1.4 and σ y =2.5 m a−1). As expected, the formal errors are ~3× greater in the y-direction (~north-south), due to the fact that both ascending and descending interferograms are more sensitive to motion in the x-direction (~east–west). The balance-velocity tie-point differences, however, are less than a factor of 2 greater in the y-direction, which may indicate that uncertainty associated with balance velocities, which should be isotropic, represents a significant part of the difference. Thus, at worst the phase errors are 2.5 m a−1 but in actuality may be nearer to 1 m a−1.
3.3. Feature tracked landsat 8 data
We downloaded all of the available 2014 and 2015 Landsat 8 images for Greenland, which we visually inspected to discard images with little cloud-free area. Next, we applied our matching algorithm to all of the same-path-row pairs that we could form with temporal separations ranging from 16 to 176 days. We culled these results to remove pairs with a low success rate in terms of either poor coverage or excessive errors. From this dataset we retained 14 224 pairs that went into producing the velocity map shown in Figure 2c.
As with the SAR data, Landsat provided the best results in the northern regions of the ice sheet, which can partially be attributed to the greater degree of overlap at higher latitudes (Fahnestock and others, Reference Fahnestock2016). In the south the more temporally varying surface conditions that affect the radar also produce poorer results for the optical images. Nevertheless, Landsat 8 produced more complete coverage than the SAR, largely due to the more comprehensive imaging campaign rather than as an intrinsic advantage of the sensor (e.g., the Sentinel 1A/B SARs are now collecting comparable coverage).
The Landsat 8 data produce larger differences with control points than either the speckle-tracked or phase data. Across all of the control points, the differences range from 3.5 to 7.5 m a−1, compared with a range 2.5–5.2 m a−1 for the speckle-tracked data. It is important to note that these differences are not direct measures of Landsat 8-versus-SAR quality since the results also reflect the number of independent estimates used to produce each mosaicked result.
3.4. Full mosaic
Figure 3 shows the complete mosaic formed as the error-weighted average of the results shown in Figure 2, which is also available online at the National Snow and Ice Data Center (NSIDC) (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2016b). This map provides virtually complete coverage of Greenland ice-sheet velocity. It is posted at 250 m spacing, but the true resolution is closer to 0.5 km. In addition to the main ice sheet, the map captures flow for many of the small ice caps and glaciers. There are few visible artifacts, with the exception of some errors that are visible along the main divide for the southern portion of the ice sheet. These errors are the result of insufficient ALOS data collection and poor correlation of the 24-day RADARSAT data.

Fig. 3. Final velocity mosaic formed as an inverse-error-weighted average of the results shown in Figure 2. This map is freely distributed through the National Snow and Ice Data Center (http://dx.doi.org/10.5067/QUA5Q9SVMSJG).
Comparison of the full map with the GPS points yields σ x = 3.7 and σ y = 3.8 m a−1, some of which, as noted for the earlier comparisons, may be due to actual change. To investigate these differences further, Figure 1 shows where (large red dots) the difference, | v − v t |, exceeds 7.5 m a−1 (~2σ). In general, these points cluster in regions where we might expect some amount of change based on the large changes farther downstream (Rignot and Kanagaratnam, Reference Rignot and Kanagaratnam2006; Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010a). When we discard these outliers, the differences are substantially smaller (σ x = 2.1 andσ y=2.8 m a−1) and agree well with the formal error estimates.
For the comparison with balance velocities, we also applied a 7.5 m a−1 threshold to discard outliers. As indicated in Figure 1, all of the poorer quality points (small red dots) are in the southerly regions (<68°N) where there are visible artifacts. The number of points in the north is large, so discarding these southern outliers only makes a small change, yielding σ x = 1.3 and σ y =2.0 m a−1. For the rock control points, the differences are 2.0 and 3.2 m a−1 for the x and y components, respectively. The larger errors on rock relative to the interior generally reflect the lack of phase data in the off-ice solution.
To summarize the overall quality of the mosaic based on our comparison with control points and the formal errors, the typical range of errors for each component is 1–3 m a−1, although in some regions, principally the southern third of the ice sheet, the errors may be larger. Most of the control points are from slow-moving regions (<100 m a−1). While the formal errors in Table 2 include the 3% error for the surface-parallel flow correction, most of the regions in the comparison are slow flowing so its contribution to the total error is small. For faster moving regions (>100 m a−1), the 3% error will be the dominant source of error.
4. DISCUSSION
By combining data from many sources, we have produced one of the most complete and accurate maps for Greenland (see also a similar products produced by Mouginot and others, Reference Mouginot, Rignot, Scheuchl and Millan2017), with errors in the interior of generally <3 m a−1 and likely approaching 1 m a−1 over much of the ice sheet. By including all of the data we could acquire, the mosaicked map represents an approximate average of the decadal velocity for the majority of the ice sheet. For the interior, there seems to be little variation at the decadal scale as indicated by the generally good agreement of the control points with the mapped velocity. For the outlet glaciers with temporally varying speeds, there are generally sufficient data such that the map represents a reasonable multi-annual/multi-season average of speed, albeit without a well-resolved time stamp. For many applications (e.g., initializing a multi-decadal model run), the benefit of complete coverage outweighs the loss of temporal resolution. For those needing better temporal resolution, the majority of the source data is available at NSIDC (http://nsidc.org/data/measures/gimp).
Ideally, we would have used a different set of points for validation (e.g., Table 2) than those used for control. As noted above, we opted to use all of the points as a source control to achieve the best possible accuracy. Because a large number of points is used in each fit, a few spurious points should not greatly skew our results. Variation in speed of the control points over time, however, could influence our results. Such variations do not occur for the rock points and are unlikely to occur for the balance velocities, which are located on relatively stable divides. Thus, only the GPS points along the 2000 m contour could potentially skew the solution. In general, however, the number of GPS points for any individual baseline solution is small relative to the number of exposed rock and balance-velocity control points. Moreover, the mosaic is produced using radar swaths with a variety of geometries. As a result, if the GPS points skewed a particular swath, then it is likely that overlapping swaths would have different biases, leading to discontinuities in final map. We find few such discontinuities, indicating any biases introduced by the GPS points are small.
Examining the GPS points, we find that most of the GPS points match the mapped speeds to within roughly the level of measurement uncertainty (1–3 m a−1), which appears to confirm our assumption of little bias. Most of the points where the differences are substantially larger (large red dots in Fig. 1) are located at the upper ends of fast flowing outlet glaciers where actual changes may have occurred. (We assumed this would be the case for Jakobshavn Isbrae and did not use points near its drainage for control.) We note, however, that while many of the largest differences occur in the southeast where many glaciers have accelerated, this region is also the area of greatest noise, which could account for some or all of the difference. Furthermore, given the high accumulation in this region, we cannot rule out the possibility that some of the differences are related to our use of a surface-parallel-flow assumption.
When the ice sheet is in equilibrium, the submergence/emergence velocity is the speed at which the surface of the ice sheet must move up or down vertically to accommodate melt (negative SMB) or new snowfall (positive SMB) to maintain a steady-state profile (Cuffey and Paterson, Reference Cuffey and Paterson2010). As noted above, in applying a surface-parallel flow assumption, we assume that the influence of the submergence/emergence velocity is small. For bare-ice regions in equilibrium, the emergence velocity should equal the ice-equivalent SMB. In the dry snow zone, the submergence velocity at the surface should equal the snow-equivalent SMB (~2.5 × SMB). Water-equivalent SMB varies by ~±4 m a−1 over the ice sheet (Ettema and others, Reference Ettema2009). Consequently, factoring in the SAR viewing geometry and firn densification, the errors due to the surface-parallel flow assumption could be as large as ~10 m a−1 (Reeh and others, Reference Reeh, Madsen and Mohr1999).
Fitting for the baseline using control points removes some of the error caused by deviations from surface-parallel flow. For example, if the SMB signal was uniform over an entire SAR scene, the effect of the submergence/emergence velocity would be cancelled implicitly as part of the baseline solution. Where SMB does vary spatially, we expect our linear or quadratic fit for the baseline to partially compensate for this error. With this compensation, these errors should be small (<1 m a−1) for majority of the ice sheet where magnitude of the SMB is <1 m a−1. In areas with strong and variable accumulation such as the southeast, however, such errors could be substantially larger. As noted above, such errors could be a contributing factor to the generally larger differences between the map and GPS points in the southeast.
The NASA ISRO (Indian Space Agency) SAR (NISAR) mission has a requirement to map interiors of the ice sheets with an accuracy of 1 m a−1 for each horizontal component. At this level of error, deviations from surface parallel flow could be significant even in areas of moderate accumulation. There has been substantial progress in understanding and correcting for the effects of accumulation and firn compaction on altimetry data (Helsen and others, Reference Helsen2008). In principle, such models can be used to correct for the submergence/emergency velocity. Unfortunately, the problem of correction for SAR is complicated by the fact that the radar signal can penetrate the firn by up to tens of meters at C- and L-band, particularly in dry-snow or bare-ice regions (Rignot and others, Reference Rignot, Echelmeyer and Krabill2001). As a result, the correction should be applied to the vertical velocity of the ‘dielectric surface’ (center of volume scattering region) rather than the true surface. Penetration depth can be difficult to estimate, adding uncertainty to the submergence/emergence velocity correction. More research is needed to refine such a correction, which is beyond the scope of the work presented here. We note, however, that even a fairly ad hoc correction would reduce this error. For example, just using the ice-equivalent submergence/emergence velocity (i.e., ignoring firn compaction) would compensate for half or more of the error relative to the uncorrected case in regions where there is substantial penetration.
We employed both SAR interferometry and speckle-tracking as well as optical data to measure ice-sheet velocity. The data we produced provides some information about the relative quality of the different types of data, though care needs to be applied in interpreting the results (e.g., Table 2) because different amounts of data were used for each method. It is clear that where the technique was applied, SAR interferometry with phase from crossing orbits provides both the greatest accuracy and best resolution (~100 m though in some cases we applied additional smoothing). The phase data are relatively robust with respect to ionospheric disturbance, and methods have been developed to further reduce such noise (Liao and Meyer, Reference Liao and Meyer2016). There are several limitations, however, in applying InSAR for measuring ice-sheet velocity. First, InSAR requires more extensive coverage to acquire images from crossing orbits. With the 24–46 day intervals we used, only relatively slow speeds (<100 m a−1) can be measured (e.g., Fig. 2b). Finally, data collected at C-band does not correlate well, leaving large gaps in coverage. Future sensors such as NISAR are designed to overcome many of these limitations, which will allow mapping of all but the fastest moving areas (~>500 m a−1) with InSAR.
In principle both speckle and optical-feature tracking are limited by the sensor resolution. Although the width of the correlation peak varies from point to point, generally cross correlation can determine displacement to within ~1/20 of a pixel, which yields quantization error of
![]() $\sigma = \left( {20\sqrt {12}} \right)^{ - 1} $
pixels. This estimate is a slightly more than that used by Mouginot and others (Reference Mouginot, Rignot, Scheuchl and Millan2017), but we reach a similar conclusion. Displacement accuracy then depends on the pixel size of the sensor. For Landsat 8 the pixel spacing is 15 m, which yields quantization errors of ~4.9 to 1.6 m a−1 for intervals ranging from 16 to 48 days. Similar calculations applied to the direction with the coarsest resolution yields errors of 0.9 m a−1 for 11-day TerraSAR-X, 1.6 m a−1 for 24-day RADARSAT, and 0.9 m a−1 for 46-day ALOS. For both SAR and Landsat 8, these estimates for single pairs are considerably smaller than the differences with control points (Table 2), indicating quantization is not the dominant source of error.
$\sigma = \left( {20\sqrt {12}} \right)^{ - 1} $
pixels. This estimate is a slightly more than that used by Mouginot and others (Reference Mouginot, Rignot, Scheuchl and Millan2017), but we reach a similar conclusion. Displacement accuracy then depends on the pixel size of the sensor. For Landsat 8 the pixel spacing is 15 m, which yields quantization errors of ~4.9 to 1.6 m a−1 for intervals ranging from 16 to 48 days. Similar calculations applied to the direction with the coarsest resolution yields errors of 0.9 m a−1 for 11-day TerraSAR-X, 1.6 m a−1 for 24-day RADARSAT, and 0.9 m a−1 for 46-day ALOS. For both SAR and Landsat 8, these estimates for single pairs are considerably smaller than the differences with control points (Table 2), indicating quantization is not the dominant source of error.
Examining the residuals after fitting for control points of 2054 16-day Landsat 8 pairs yields an average residual of 48 m a−1 or equivalently 2.1 m of displacement for each component. For 32-day intervals, the displacement residual increases to 2.6 m, but the longer interval reduces the velocity residual to 30 m a−1 in each direction. Because the results can be skewed by outliers, the corresponding median errors of 35, and 22 m a−1 for 16 and 32 days, respectively, may better represent the typical errors. These values are considerably larger than the residuals (Table 2) for the Landsat 8 mosaic (Fig. 2c), which were achieved by discarding the pairs with largest residuals (~19% of total processed pairs), using pairs with the longest available temporal separation (up to 176 days), and averaging the results from many estimates (14224 pairs). They are also considerably larger than the precision (17 m a−1 for 16-day pairs) estimated for Landsat in Antarctica (Mouginot and others, Reference Mouginot, Rignot, Scheuchl and Millan2017). The more optimistic results, however, were for the more stable Antarctic Plateau, and the same group attained similar results to ours for Greenland (Mouginot pers. comm. 2017).
We performed a similar accuracy analysis of 1550 TerraSAR-X pairs, mostly (>90%) with 11-day intervals, which yielded average residuals of 5.0 and 8.3 m a−1 for the range and azimuth directions, respectively. There are some large outliers, so as with Landsat 8, the corresponding median values of 2.4 and 4.9 m a−1 are probably better indicators of performance. These results suggest nearly an order of magnitude better accuracy with finer temporal resolution (11 vs ≥16 days) and spatial resolution. Due to its operating frequency, the TerraSAR-X data only have negligible error due to ionospheric artifacts.
We did not perform a similar analysis for RADARSAT and ALOS data because the baseline fits were not based on a consistent set of control points, unlike the TerraSAR-X data, which were all nearly completely controlled by exposed bedrock. Based on our analysis of annual mosaics and accounting for the averaging, single RADARSAT and ALOS estimates generally have average accuracies of 10 m a−1 or better. As noted previously, error can be substantially larger in areas where ionospheric artifacts are present.
When and where available, SAR data generally exceed the accuracy provided by Landsat 8 by a factor of 2 or more. There are several instances, however, in which Landsat 8 data were collected and there is no corresponding viable SAR data. For the velocity maps we produced, Landsat 8 helped fill gaps where there were no SAR data despite 20 years of collection. As we and others have demonstrated (Mouginot and others, Reference Mouginot, Rignot, Scheuchl and Millan2017), however, both types of data can be seamlessly blended. Even though Landsat 8 may be noisier in most cases, when the data are averaged with an inverse-error weighting, all additional data improve the final result.
5. CONCLUSION
Our mosaic with accuracies of 1–3 m a−1 in slow moving regions required 20 years of SAR and optical data collection to produce. Although the map approximates a decadal average, many of the data used to produce it have been distributed as maps with annual (Joughin and others, Reference Joughin, Smith, Howat and Scambos2010b) to sub-monthly resolution (Joughin and others, Reference Joughin, Howat, Smith and Scambos2011b), particularly for rapidly changing, fast flowing outlet glaciers (Joughin and others, Reference Joughin, Smith, Howat and Scambos2010b; Moon and others, Reference Moon, Joughin and Smith2015). The comprehensive map produced from the combination of these data, however, is important result for studies where accuracy and spatial coverage are more important than temporal resolution.
Our efforts in producing this map have been limited by the relatively sparse collection of data over the entire ice sheets (many outlet glaciers have been more regularly sampled). This situation has changed recently with the routine collection of data over Greenland by the Landsat 8 (Fahnestock and others, Reference Fahnestock2016) and Sentinel 1A/B satellites (Nagler and others, Reference Nagler, Rott, Hetzenecker, Wuite and Potin2015). Operating C-band, the Sentinel 1A/B SARs collect data roughly comparable with RADARSAT 1, albeit with poorer azimuth resolution and interferometric phase that is problematic for ice-sheet mapping. Such deficiencies can be overcome to a large extent by averaging the vast amount of data that is now routinely collected. Measurements of ice flow will be further improved with the launch of the NISAR instrument in 2021, which will provide full ascending and descending coverage of the ice sheets every 12 days. Collectively, the constellation of current and future satellites will provide greatly improved time series of ice flow variation in both Greenland and Antarctica, which are crucial to understanding current and future contributions of ice flow dynamics to sea-level rise.
ACKNOWLEDGEMENTS
The data described in this paper were produced with support from the NASA MEaSUREs program (NASA grants NNX08AL98A and NNX13AI21A). The RADARSAT data were acquired by the Canadian Space Agency (CSA), and the PALSAR data were acquired by the Japanese Space Agency (JAXA). The RADARSAT data through 2010 and the ALOS-PALSAR data were archived and delivered by the Alaska Satellite Facility (ASF). The 2012/13 RADARSAT data were archived and delivered by CSA. The German Space Agency (DLR) provided the TerraSAR-X and TanDEM-X data. The full velocity mosaic is available through NISDC (http://dx.doi.org/10.5067/QUA5Q9SVMSJG). All source data are available from their respective space agency and the ALOS-PALSAR and RADARSAT data are also available through ASF. The Landsat 8 were provided by US Geological Survey (USGS) and distributed via Google.







