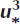The atmospheric snow-transport model: SnowDrift3D

Abstract

SnowDrift3D, a high-resolution, atmospheric snow-transport model, is presented for the first time. In contrast to most state-of-the-art snowdrift models, atmospheric particle transport, i.e. saltation and suspension, is accounted for by one passive transport equation. The model uses unsteady wind fields (spatial resolution of up to 2 m) computed with an atmospheric computational fluid dynamics model that is directly connected to the numerical weather prediction model ALADIN. Sensitivity runs show that (1) the saltation mass flux is a function of cubic shear velocity, , (2) the model is marginally sensitive to the grid spacing at high resolutions (up to 2 m), (3) the model computes the redistribution of snow at high resolution in real time on dual core personal computers and (4) the changing topography of the snow cover should be included in cases of local erosion or deposition of a large amount of snow. Finally, we present a comparison of modeled and measured snow distributions obtained by terrestrial laser scanning showing area-wide linear correlation up to R = 0.33.

1. Introduction

The topic of environmental snow transport has attracted many researchers over the past few decades. In alpine areas, drifting and blowing snow have a significant influence on avalanche danger, necessitate expensive road clearing and create large snow cornices on mountain ridges. A great number of numerical models with varying degrees of numerical and physical complexity have been developed to model blowing and drifting snow in tundra, scrubland or complex, steep alpine terrain. To the authors’ knowledge, only one of these models (Alpine3D (developed at the Swiss Federal Institute for Snow and Avalanche Research); Mott and others, 2010) has been satisfactorily validated against area-wide snow depth measurements. On the one hand, this might be explained by the complexity of the physical process (extensively discussed by Lehning and others, 2008). On the other hand, measurement methods providing accurate area-wide snow heights have only recently become available, including terrestrial laser scanning (TLS; Prokop, 2008; Prokop and others, 2008). In this introduction, we discuss important aspects of the numerical modeling of blowing and drifting snow. Similarly to Liston and others (2007), we distinguish numerical snowdrift models tailored to either individual storm events or the entire snow season. The SnowDrift3D model we present is primarily focused on single events.

The most sensitive transport modeling parameter is the driving wind field, or more specifically, the airborne shear stresses acting on the snow cover (Liston and others, 2007; Lehning and others, 2008; Bernhardt and others, 2009). Wind-field data may be obtained by simple interpolation from observations (i.e. measurements or numerical weather models) using mathematical functions derived from terrain topography (e.g. Ryan, 1977; Liston and others, 2007). However, in alpine terrain, meteorological data are typically scarce and an extrapolation of these data to the area of interest can lead to homogeneous wind fields unsuitable for accurate snowdrift modeling in complex terrain (Bernhardt and others, 2009). Gauer (2001) applied the computational fluid dynamics (CFD) solver CFX, which utilizes the compressible Navier–Stokes equations, to compute the wide-range atmospheric flow. In contrast, others have applied atmospheric mesoscale models (e.g. MM5 (the fifth-generation Penn State/NCAR Mesoscale Model; Grell and others, 1995) and ARPS (the Advanced Regional Prediction System; Xue and others, 2000), which are specifically designed for the numerical simulation of environmental flows. For example, Bernhardt and others (2009) coupled SnowTran-3D (Liston and others, 2007) with MM5, and Lehning and others (2008), Mott and Lehning (2010) and Mott and others (2010) used the wind field from ARPS in driving Alpine3D. Raderschall and others (2008) suggested from sensitivity studies that a minimal grid resolution of 25 m is necessary to resolve the overall structure of the wind field, as well as characteristic flow features in steep terrain, i.e. speedup of the flow over ridges, flow separation, flow blocking and recirculation downwind of the ridge. In the current configuration, Alpine3D uses wind fields down to a vertical and horizontal grid spacing of 5 m to drive the environmental snow transport. In contrast, the spatial resolution of MM5 is not sufficient to resolve such small-scale flow features and, hence, the wind fields are kinematically downscaled to fine resolution. This procedure inevitably suppresses dynamical flow effects, which are not already present in the input fields (Schneiderbauer and Pirker, 2010). Furthermore, in SnowTran-3D, simplified drift profiles are introduced instead of an explicit analysis of the turbulent surface boundary layer. These simplifications may inevitably lead to an inaccurate evaluation of the wall shear stresses, which is directly connected to the amount of aerodynamic entrainment (Anderson and Haff, 1991; Shao and Li, 1999) and the saltation mass fluxes (Pomeroy and others, 1993; Clifton and Lehning, 2008). Explicitly accounting for the boundary layer within the wind-field generation, as in ARPS, may also lead to inaccurate estimations of the wall shear stress, due to the simplified explicit logarithmic law-of-the-wall (e.g. Gauer, 2001; Clifton and Lehning, 2008; Lehning and others, 2008). In the wind-field modeling mentioned above, with typical values of boundary layer conditions h ⁺ > 60 (where h ⁺ = ρ _a u_∗h _c/μ _a with ρ _a the density of air, h _c the distance of the centroid of the first cell adjacent to the ground and μ _a the molecular viscosity of air), the shear stress is an implicit function of the friction velocity, u _* (Prandtl and others, 1990, ch. 4).

A further challenge of modeling wind flow in complex terrain is the uncertainty connected with boundary and initial conditions. The main concern is how to incorporate remote meteorological data into the definition of the driving wind field. Gauer (2001) simply extrapolated wind speed and velocity directly from meteorological stations to the inflow boundary. Although it was not clearly stated how this extrapolation was realized, modeled and measured values were correlated for the one specific drift period. Bernhardt and others (2009) avoided the above extrapolation in a rather simple and elegant way: a wind-field library for different wind speeds and directions was created, and the specific wind field best matching the meteorological observations was taken ‘out of the library’ to compute the environmental snow transport. However, huge computational effort is required to create the library, especially when applying the model to a new topography. Considerable computer memory is also required, given that all wind fields complying to all possible weather situations have to be computed and stored. Such a strategy may become unfeasible if the temperature of the flow is also taken into account, as it would induce an exponential growth of the number of required wind fields in the library. The wind field and temperature distribution are tightly coupled through gravity winds, thermal air currents, thermal instabilities, etc. Within Alpine3D, periodic boundary conditions can be set (Raderschall and others, 2008; Mott and Lehning, 2010) and the wind field is initialized with a standard logarithmic wind profile within the atmospheric boundary layer. Above the boundary layer, a layer with vertically constant free-stream velocity, u _∞, is assumed. This strategy may be more flexible than the method of Bernhardt and others (2009); however, the adapted wind field (characterized by speed-up at ridges, channeling, etc.), which is supposed to accurately correlate to measurement data in the area of interest, is strongly coupled to the choice of u _∞ This, in turn, requires knowledge about the correlation between wind speeds at the locations of the measurements and u _∞ For example, this dependency is given by a wind-field library or can be computed directly using an optimization approach (Schneiderbauer and Pirker, 2010).

For modeling purposes, it is typical to differentiate between grains transported in saltation and in suspension. Strictly speaking, there is a third transport mode known as creeping or reptation, but this is commonly neglected in numerical snowdrift models, since its contribution is small compared to the other transport processes. Saltation occurs in a thin layer directly above the snow cover, and the snow grains follow ballistic trajectories. Liston and others (2007), Bernhardt and others (2009) and Naaim-Bouvet and others (2010) accounted for saltation by the semi-empirical relation of Pomeroy and Gray (1990), which uses a linear scaling of the mass flux with the friction velocity. However, this is a contradiction to the cubic dependence suggested by Clifton and Lehning (2008). A more detailed, albeit computationally more demanding, model of mass transport in saltation was presented by Gauer (2001). Based on the essential characteristics of the trajectories of saltating grains (i.e. particle deposition, rebound and ejection of other grains at impact), two-dimensional transport and momentum equations for the saltation layer were deduced. More recently, Doorschot and Lehning (2002) and later Clifton and Lehning (2008) introduced a formally explicit, computationally effective local momentum balance to obtain the particle flux in saltation (this is the scheme used in Alpine3D). This saltation model also suggests that the mass flux is a cubic function of the friction velocity. In most of the models that include saltation and suspension independently, artificial boundary conditions are introduced to model the mass exchange between both transport modes. Shao and Li (1999) and Nemoto and Nishimura (2004), however, computed the trajectories of individual grains in a Lagrangian frame rendering the above numerical separation unnecessary. In this work, a Lagrangian stochastic theory is used to account for turbulence effects on the trajectories of the snow grains. Although their approaches may be characterized as the most physically based, they are not applicable in the context of alpine snow transport and operational use.

Turbulent suspension occurs in the layers above saltation. The appropriate modeling of turbulence requires a sophisticated turbulence model and the definition of relevant boundary conditions. Equally important is the influence of turbulence on the suspended snow grains. One family of turbulence models is based on Reynolds averaging (e.g. k–∊ type) (see Kim and Patel, 2000; Kristóf and others, 2009; Schneiderbauer and Pirker, 2010). These can be applied to atmospheric flows where the Reynolds number, Re, is . An alternative to the k–∊ type turbulence models involves applying large eddy simulation (LES) to atmospheric flows (Wood, 2000; Porté-Agel and others, 2001; Kleissl and others, 2006; Raderschall and others, 2008). The atmospheric mesoscale model ARPS utilizes LES in which a one-equation subgrid model accounts for the subgrid turbulence. This requires capturing the unsteady dynamics of the turbulent eddies by sufficiently small time-steps (i.e. Courant number, C < 1) in the numerical simulation, a step which increases the computational effort. As most snowdrift models assume mean flow properties, a time-averaged wind field has to be computed from the time-dependent LES solution. To overcome such long time integrations Lehning and others (2008) and Raderschall and others (2008) suggested that the initial adaption of the flow, i.e. at short integration times before turbulent structures develop, is a good approximation for the time-averaged LES wind field. This approximation is questionable with regard to recirculation downwind of ridges which would also be visible in time-averaged flows, in contrast to the initially adapted wind fields.

The coupling of turbulence on the transport of suspended grains is also important. Liston and others (2007) modeled equilibrium suspension by a one-dimensional diffusion equation and ignored the lateral advective effects. This equilibrium assumption is doubtful for steep terrain. Déry and others (1998), Gauer (2001), Lehning and others (2008) and Naaim-Bouvet and others (2010) used a three-dimensional transport equation, in which the influence of the turbulent fluctuations is modeled by a simple diffusion approach, thereby overcoming the limitations of the model of Liston and others (2007). This simplification of the suspension process should be sufficient for the needs of the numerical modeling of blowing snow, since diffusion is mostly driven by the vertical gradient of the particle volume fraction. Horizontally, the transport is advection dominated (and the gradient in horizontal direction vanishes at equilibrium suspension). Such a modeling approach should result in approximately linear scaling of the suspension mass flux with wind speed (Lehning and others, 2008; Dadic and others, 2010). However, diffusive transport is strongly affected by turbulent viscosity, requiring the appropriate definition of turbulent boundary conditions, as used by Schneiderbauer and Pirker (2010; and references therein). Employing periodic boundary conditions, like Raderschall and others (2008), is an elegant way to generate appropriate turbulence boundary profiles, given that the integration time is long enough to allow the atmospheric boundary layer to fully develop.

The changing topography of the snow cover due to ongoing snowdrift should also be considered in numerical models. The snow depth increases in deposition areas and decreases in erosion zones, influencing the local velocity field. Hence, modification of the wind field causes time-dependent spreading of these zones (Gauer, 2001; Schneiderbauer and others, 2008; Schneiderbauer, 2010). Mott and others (2010) reported a significant influence of the topography on the snowdrift pattern, based on a comparison of snowdrift modeling using a summer and a winter digital elevation model (DEM). Gauer (2001) and Schneiderbauer and others (2008) simulated the changing topography by moving the gridpoints spanning the snow cover without explicitly paying attention to the associated distortion of the above volume mesh; however, notably stretched cells or even negative cell volumes may appear. h ⁺ boundary layer conditions must be met when using the logarithmic law-of-the-wall, but this may be violated with increasing deformations. Even small displacements affect the quality of the volume mesh and lead to reduced accuracy and finally to numerical instabilities.

In this paper we introduce a new numerical model (SnowDrift3D) for blowing and drifting snow. In developing this model, the long-term goal was to consider the issues discussed above and to integrate the most appropriate modeling schemes without expecting to provide a solution for them. An overview of the model characteristics and implementation is given below. We apply the CFD solver FLUENT to generate the driving microscale atmospheric wind field, temperature and turbulence distribution. Schneiderbauer and Pirker (2010) showed that standard CFD can be adapted to obtain sufficiently accurate atmospheric flows. A short summary of necessary model adaptions is given in the Appendix, and the spatial boundary conditions are discussed in section 5.2. Moreover, the k–∊ model used (RNG; Yakhot and Orszag, 1986) meets the demands of turbulence modeling in mountainous regions (Kim and Patel, 2000). Furthermore, the whole wind-induced snow transport (i.e. saltation and suspension) is covered by a passive transport equation, whereas a diffusion approach accounts for turbulent suspension (section 2). Sub-models account for erosion and sedimentation of saltating snow grains (section 3). These sub-models are founded in the work of previously published literature. Section 4 deals with details of the model implementation: (1) the timescale of the atmospheric flow is an order of magnitude higher than the timescale of the erosion and sedimentation processes (a semi-implicit Euler method is utilized to integrate the amount of eroded and accumulated snow in time during a fluid time-step, which saves a significant amount of computational time); (2) since the passive transport equation for the snow grains does not incorporate fluid momentum loss due to saltating particles, a local saltation momentum balance is solved to obtain the excess airborne shear stress for aerodynamic entrainment; (3) the implicit logarithmic law-of-the-wall is directly evaluated to compute the wall shear stress, instead of using simplified versions of this relation; (4) an arbitrary Lagrangian Eulerian method, which conserves the h ⁺ condition for the numerical grid, includes the changing topography. Sensitivity runs (section 6) show the dependence of the saltation mass flux on wind speed, the influence of the grid resolution on the final snowdrift pattern and the impact of the time-dependent change in the topography due to erosion and sedimentation. Finally, the results of SnowDrift3D are compared to snow height measurements obtained by TLS (Prokop, 2008) in section 7.

2. Snow Transport Equation

Following Schneiderbauer and others (2008), we consider the snow particles in saltation and suspension as one continuous phase. The saltation and the suspension layers are not separated numerically as they are in the work of Gauer (2001), Doorschot and Lehning (2002), Liston and others (2007), Lehning and others (2008), Mott and Lehning (2010) and Naaim-Bouvet and others (2010). The physical difference between saltation and suspension as transport modes lies in the properties of particle trajectories: in saltation, snow particles follow ballistic trajectories as prescribed by their ejection angle and speed; in suspension the motion of the snow grains is affected by the turbulent eddies superimposed by the terminal falling velocity. Snow transport is generally dependent on influencing flow factors, average particle properties (size, shape, etc.) and gravity. The degree of turbulence at the height of the saltation layer is particularly important in determining the number of resuspended snow grains. The ballistic particle trajectories are interrupted by the turbulent velocity fluctuations (i.e. the motion of the turbulent eddies).

The velocity of the snow phase, u _p, can be calculated as follows for a typical ice particle, assuming a density ρ _p ≈ 917 kg m⁻³ and a diameter d _p ≈ 300 μm (as Equation (A2))

(1)

where g = (0, 0, −g)^T. The above equation implies that all saltation activity is located in the cell layer adjacent to the snow cover; snow transport elsewhere is referred to as suspension. In Equation (1), u _a represents the velocity of the wind field of an arbitrary cell center, the flow velocity at the height of the saltation layer and g the standard acceleration due to gravity. Furthermore,

(2)

denotes the terminal falling velocity of spherical snow grains including buoyancy, where C _D is the drag coefficient depending on the particle shape and ρ _a the density of air. Note that the height of the saltation layer, h _s, appearing in Equation (1) is similar to that of Doorschot and Lehning (2002) or Lehning and others (2008), which is computed from the initial velocity of entrained grains (Equation (33)). It is known from previous work (Clifton and Lehning, 2008) that the saltation flux rate is a cubic function of wind speed. It is expected that this relationship would be produced in the saltation modeling presented here and, indeed, this is shown in section 6.1.

From the above, it can be argued that the Reynolds averaged transport equation for the volume fraction of snow particles, α, is

(3)

where superscripts ‘E’ and ‘Ej’ indicate aerodynamic entrainment and ejection, respectively. Detailed derivations of the transport equation (3) and the resulting corrections to the momentum equation of the wind field are given in the Appendix. The source terms, S ₊ and , account for accumulation and erosion events discussed in section 3. Note that such a transport equation is frequently used to model the advective transport of suspended snow in other snowdrift models (Gauer, 2001; Lehning and others, 2008; Naaim-Bouvet and others, 2010).

From the discussion in the introduction it is concluded that the turbulent transport of suspended grains can be described by the simple diffusion term appearing in Equation (3). The diffusion coefficient, Γ, is parameterized as

(4)

Here μ _t indicates the turbulent eddy viscosity, ∊ the turbulent dissipation rate appearing in the RNG k–∊ model (Yakhot and Orszag, 1986), C _μ, = 0.09 a constant and Sc_t ≈ 1 the turbulent Schmidt number. Evaluating Equation (4) for the cell layer adjacent to the snow cover with height h _c gives

(5)

which corresponds to the boundary value proposed by Déry and others (1998). Note that we use

(6)

for values of k and ∊ at the numerical cells adjacent to the snow cover, where u_∗ denotes the friction velocity, , with τ _a the airborne shear stress. Furthermore, h represents the distance from the ground surface along the direction of the unit surface normal, h ₀ the physical surface roughness height and κ = 0.4 the von Kármán constant.

Note that the mass exchange between saltation and suspension is part of the solution of Equation (3). Numerically the mass transfer rates, S_↑ (from saltation into suspension) and S_↓ (from suspension into saltation), can be computed from

(7)

where z is the coordinate in the vertical direction and S_i is in kg m⁻³ s⁻¹.

3. Snow Erosion and Sedimentation

We use the parameterization of the erosion and sedimentation processes given by Schneiderbauer (2010), who provides a validation of that parameterization by a wind tunnel experiment. The following gives a brief overview of the erosion and accumulation models.

There are two main modes of snow grain erosion: aerodynamic entrainment and particle splashing. Anderson and Haff (1991) estimate that the number of entrained grains per unit time and unit area, N _E, linearly depends on the excess airborne shear stress, τ _E, which is used by Gauer (2001) and Doorschot and Lehning (2002). More recently, Shao and Li (1999) proposed that the proportionality factor, , appearing in the formula of Anderson and Haff (1991) is a function of the particle diameter and the excess airborne shear stress. Taken together, this gives

(8)

where ζ _E is dimensionless and τ _t denotes the fluid threshold. For particles with a diameter d _p = 300 μm, Shao and Li (1999) claimed that ζ _E = 1.73 × 10⁻³; however, Schneiderbauer (2010) found that ζ _E(d _p) approximately scales as 5.19 × 10⁻⁷ d _p ^{− 1} Consequently, the mass source (kg m⁻³ s⁻¹) appearing in Equation (3) reads as follows when accounting for aerodynamic entrainment:

(9)

where A denotes the area and V the volume of a cell adjacent to the snow cover. In addition, Shao and Li (1999; and references therein) suggest that the initial velocity of entrained grains is in proportion to the friction velocity

(10)

where ξ _E is a dimensionless parameter. Equally important, the formulation of Schmidt (1980) for the fluid threshold is used, where a packing ratio of η = 0.21 and an angle of repose of β = 33° are assumed. The cohesion force, F _C, appearing in this formulation of the fluid threshold is modeled using the data of Hosler and others (1957), who found that cohesion between snow particles at 0°C is nine times that at −15°C, which gives

(11)

where T denotes the temperature (°C). Furthermore, we assume a temperature of −15°C for the cohesion force, F _C,_−15°, at ice saturation

(12)

For snow particles with a diameter d _p = 300 μm, the cohesion force, F _C,−15° , is approximately 2.6 × 10⁻⁸ N. However, the influence of the structural properties of the snowpack is not addressed in the presented model at this time. The coupling of snowdrift to snowpack models has been dealt with in detail by, for example, Durand and others (2005) and Lehning and Fierz (2008), though none of the other work cited in this section has included this coupling.

When a saltating grain collides with the snow cover, it either ejects other grains, rebounds or remains trapped. In contrast to Gauer (2001), Andreotti and others (2002) and references therein suggesting that the number of ejecta per impact N _Ej scales linearly with the impact speed u _p,I, we follow Andreotti (2004) claiming that

(13)

Here the dimensionless parameter, ζ _I, defines a velocity scale and u _p,I the velocity of an impacting grain. The splashing rate (kg m⁻³ s⁻¹) is then given by

(14)

where N _I(α, t _p) = α/t _p is the number of collisions with the snow cover per saltating particle and per unit time. t_p = 2w _p,E/g denotes the average travel time of a saltating grain depending on the initial velocity, w ₀, of entrained grains. Andreotti and others (2002) estimated the initial velocity parallel to the snow cover of ejected grains as

(15)

with an ejection angle θ _Ej ≈ 45°. Here ξ _R = u _p,R/u _p,I denotes the coefficient of restitution, where u _p,R indicates the velocity of a rebounding grain. In this work, ξ _R is set equal to 0.5 after Shao and Li (1999), Gauer (2001) and Andreotti (2004).

The probability that a particle remains trapped is given by (Anderson and Haff, 1991)

(16)

with ζ _I = 10, and this equation has also been included in the drift models of Gauer (2001) and Andreotti (2004). Given the number of collisions of a grain with the snow cover per unit time, N _I(α, t _p), and the probability that a particle remains trapped at a specific impact, p _T(u _p,I), the mass source (kg m⁻³ s⁻¹) accounting for accumulation is then calculated as

(17)

4. Numerical Implementation

4.1. Semi-implicit Euler time integration subcycling scheme

If the mean particle travel time, t _p, is considered towards the limit state of vanishing friction velocity (e.g. in leeward areas) it would follow that

(18)

Despite this, during the numerical solution of the particle transport equations (3) the following relationship for the Courant number C should hold:

(19)

where U_p defines the velocity scale and L_grid the length scale of the numerical grid. Furthermore, Δt denotes the time-step size used in the numerical simulation of the wind field and snow transport. If we assume that and we are led to a maximal time-step size of Δt ≲ 1 s. Thus, the mean particle travel time, t _p, defines the upper limit for the time-step size, Δt. Consequently, if Δt exceeds the ratio p _T(u _p,I)/t _p, more than the available volume fraction of snow grains might accumulate within one time-step. Limiting Δt by t _p leads to impractically small time-steps which would considerably increase the computational time, but limiting t _p by a fixed time-step size, Δt, leads to an underestimation of the number of impinging grains, N _I(α). To solve this, we apply a semi-implicit Euler integration subcycling scheme with time-step size to compute the amount of entrained, ejected and accumulated particles, while the flow, temperature and turbulence distribution are assumed to be constant within the time Δt (C^max ≲ 1). The semi-implicit Euler integration of and α is given by

(20a)

and

(20b)

with

(20c)

where k denotes the number of the subcycling time-step. The acceleration, g(t ^(k), α ^(k)), reads as

(21)

The first term on the right-hand side of Equation (21) indicates the acceleration of the particles due to the excess airborne shear stress. That is, if τ _E does not exceed the fluid threshold, τ _t, which is evaluated at the fluid time-step l, the remaining shear stress, τ _E, accelerates the saltating snow grains. denotes the aggregate mass of particles within a control volume V. accounts for the momentum change due to the change in volume fraction induced by aerodynamic entrainment (as the initial velocity of the entrained grains in the flow direction is 0):

(22)

(The change in momentum induced by particle ejections is addressed by Equation (26).)

Reviewing Equations (9), (14) and (17), the amount of sedimentation, particle ejections and aerodynamic entrainment become

(23)

which leads to

(24)

The mass sources, , and momentum sources, , in Equations (3) and (A7) at fluid time-step l + 1 can finally be deduced from

(25a)

and

(25b)

requiring that Δt = nΔt’. Finally, the initial conditions for the volume fraction, α ^(l,0) = α ^(l), and for the velocity at the height of the saltation layer, , hold (these can be obtained from Equations (3) and (A7)).

4.2. Saltation momentum balance

Since we model the snow transport by a passive transport equation (3) and neglect the interphase momentum exchange, the wind field is not influenced by the snow grains in terms of the force required to accelerate rebounded, entrained and ejected particles. Hence, the excess airborne shear stress, τ _E, appearing in Equations (9) or (23) – the shear stress available for aerodynamic entrainment – remains unknown. Thus, we compute τ _E from a local momentum balance at the snow cover:

(26)

where τ _a(u _a) denotes the airborne shear stress, τ _R the shear necessary to compensate for the momentum loss of rebounding particles (grain shear), τ _Ej the shear required to accelerate ejected grains and τ_α the shear accounting for the gravitational force acting on the snow grains. Similarly to Gauer (2001), we use the following parameterizations of τ _R, τ _Ej and τ_α :

(27)

ϕ denotes the slope angle with respect to the flow direction (positive for downward slopes). The excess airborne shear stress, τ _E, from Equation (26) is computed as follows: First of all, the airborne shear stress, τ _a, is directly evaluated from the transcendental equation for the law-of-the-wall (Prandtl and others, 1990, ch. 4):

(28)

where denotes an empirical constant, h _c the distance of the cells adjacent to the snow cover, μ _a the molecular viscosity of air and r a roughness function given by

(29)

with the physical roughness length h ₀. Owen (1964) found that the aerodynamic roughness is proportional to

(30)

with γ ≈ 0.12. Since h ⁺ = ρ _a u_∗h _c/μ _a and r are not known explicitly, Equation (28) has to be solved iteratively, requiring the differentiation of implicit functions and possibly failing to converge. This problem may be solved by the substitutions h → Eh ⁺ and h ₀ → r to obtain an explicit form of the law-ofthe-wall (Equation (28)) as applied by Gauer (2001), Liston and others (2007), Clifton and Lehning (2008), Lehning and others (2008) and Naaim-Bouvet and others (2010):

(31)

These substitutions, however, lead to an overestimation of the increase of shear stress with increasing wind speed in the fully turbulent log region. We have chosen instead to apply a linearized implicit scheme (Lew and others, 2001; Schneiderbauer, 2010) to Equation (28) to evaluate the airborne shear stress. This linearized scheme does not lead to a significant deviation in the resulting shear stress compared to the evaluation of Equation (28) by Newton’s method (Schneiderbauer, 2010). Furthermore, to obtain an expression for the impact velocity of the saltating snow grains we follow Pomeroy and Gray (1990), who suggest that the horizontal particle velocity within the saltation layer is constant with height. We also assume that the flow velocity matches the particle velocity at the top of the saltation layer with height h _s implying

(32)

Typically h _s is (Anderson and others,1991) and is derived from Equation (10), which gives

(33)

Greeley and Iversen (1985) estimated the height of the saltation layer and therefore, . Note that the determination of ξ _E strongly depends on an accurate evaluation of u_∗ .

As a result of the assumptions made in Equation (1), the height of the first cell layer adjacent to the snow cover, h _c, has to exceed h _s over the entire computational domain. In contrast, Hunt and others (1988) suggested that the logarithmic law-of-the-wall (Equation (28)) applies only within a thin layer adjacent to the surface with a height (i.e. h ⁺ condition). A computational mesh with implements the model’s prerequisites, and the flow velocity at the top of the saltation layer can then be simply computed from Equation (28) by the substitution h _s → h _c.

The shear stresses, τ _R, τ _Ej and τ_α , are computed using Equation (27). Equation (26) is treated as follows: First of all, τ_α is subtracted from the airborne shear stress, τ _a. If τ _a − τ_α < 0, no excess shear stress will be available for particle rebound, particle splashing or aerodynamic entrainment; hence, τ _E = 0 and the saltating snow grains accumulate. Otherwise if τ _a − τ_α > 0 and τ _a − τ_α − τ _R < 0, the saltating particles partly accumulate so that , and, as before, neither particle splashing nor aerodynamic entrainment occurs. As long as τ _a − τ_α − τ _R > 0 and τ _E from Equation (26) is still negative, particle erosion due to particle ejection will take place so that . Finally, in the case of τ _E = τ _a − τ_α − τ _R − τ _Ej > 0 aerodynamic entrainment will be possible after Equation (9). An overview for the evaluation of τ _E is given in Table 1. A comparable idea for solving a momentum balance as in Equation (26) is proposed by Doorschot and Lehning (2002) and Clifton and Lehning (2008). Note that τ_α , τ _R, τ _Ej and τ _E have to be evaluated at every subcycling step, k, while τ _a remains constant for Δt = nΔt’ and that and hold. In summary, aerodynamic entrainment is the initializing process for saltation since τ _E(α = 0) = τ _a and saltation will be maintained by particle ejections even if the excess airborne shear stress for aerodynamic entrainment, τ _E, is reduced below τ _t.

Table 1. Wind speeds and directions at the Kriegerhorn

Algorithm 1. Pseudocode for the evaluation of τ_E from Equation (26) within the subcycling proposed in section 4.1.

4.3. Changing topography

Following Schneiderbauer (2010), the changing topography of the snow cover is considered by an arbitrary Lagrangian Eulerian (ALE) approach. The snow depth (i.e. the sum of vertical movements) at time-step l at an arbitrary node, i, at the surface of the snowpack is given by

(34)

where the set contains all neighbor faces to node i, η defines the packing ratio of the snow cover, denotes the number of neighbor faces to node i, V_j is the volume of the cell adjacent to face j, and φ_j its slope angle. Downward movement of a node i is limited by the ground topography. Moreover, S = T_f/T_h denotes a scale factor to decouple the timescale of the flow, T_f (Equations (A1)), and the timescale of the motion of the nodes, T_h (Schneiderbauer and others, 2008; Schneiderbauer, 2010). If we consider T_h as the physical timescale, the flow field will be kept constant for a time period ST_h. Schneiderbauer and others (2008) proposed S = 100 as an upper limit, whereas in this work we generally set S = 25.

As indicated in the introduction, the mesh quality may significantly decrease when applying the ALE approach. In order to distort the interior mesh along with the snow cover while preserving the h ⁺ condition to the mesh, a Laplace equation for the nodal displacement field, δ(x, t), is solved (Schneiderbauer, 2010) by

(35)

with the Dirichlet boundary conditions

(36)

4.4. Precipitation

In addition to snowdrift, preferential precipitation has a non-negligible influence on the resulting snow depth, h _SD. This is especially true at low wind speeds, where precipitation leads to an additional contribution at upwind and downwind slopes (Lehning and others, 2008). In this work we account for precipitation utilizing a mass source in Equation (3) as follows:

(37)

where z is the height above sea level, and z _l and z _u denote a lower and an upper limit of the ‘virtual’ snow cloud. Furthermore, ϑ indicates a proportionality factor with dimensions s⁻¹ and is set to (Δt)⁻¹ . The precipitation volume fraction within the snow cloud, α _pre, can be approximated by a measured precipitation rate, Φ_pre (kg m⁻² s⁻¹), as

(38)

5. Additional Methods and Model Set-Up

5.1. Experimental set-up

The test site (Mohnensattel) is located in the vicinity of Lech am Arlberg in the Austrian Alps. Given the relevant wind direction, this area experiences typical snowdrift events, i.e. a redistribution of snow by wind over a ridge with accumulation in the leeward areas. More specifically, the dominant westerly winds cause snow redistribution that results in snow accumulation and cornice development on leeward aspects. These features are often responsible for triggering avalanches on a southeast-facing slope above a ski run. The investigated area has spatial dimensions of ∼1 km² (Prokop, 2008). The TLS measurements were performed using a Riegl LPM i800HA device (for a technical description of the TLS methodology for scanning snow surfaces see Prokop, 2008; Prokop and others, 2008). The vertical measurement accuracy, which is determined by reproducibility tests, is ∼0.05 m. At a measuring distance of 100 m the average horizontal point spacing is 0.05 m. Accurate positioning of repeated scans was achieved using a differential GPS with seven additional tie points located in the scanning area. The resulting point cloud data can then be georeferenced and registered, whereby the data points are transformed from the local coordinate system of the scanner into a referenced coordinate system. Finally, the TLS data were post-processed by applying the method of Prokop and Panholzer (2009), which utilizes RiPROFILE and ArcGIS software to obtain the final spatial snow depths. The snow depth is calculated as the vertical distance between two digital snow surface grids (or between a terrain and snow surface grid). The TLS dataset used in the present study was one of the first such datasets applied to evaluate the quality of snowdrift models.

5.2. Boundary and initial conditions

We investigate the snowdrift patterns induced by two different typical wind situations. Firstly, the absolute snow heights around the Mohnensattel, Vorarlberg, Austria (Fig. 1) are determined for 24 March 2007. The snow distribution in this case is due to prevailing westerly winds. Secondly, the redistribution of snow between 13 and 24 March 2007 is analyzed, in which case northeasterly winds and precipitation contribute significantly to the overall weather situation. In Figure 2 the distributions of wind speed and wind direction at the Kriegerhorn station (Fig. 1) for the chosen period are plotted. As can be seen in Figure 2, westerly and northeasterly winds are generally dominant. Strong westerly and northeasterly winds only prevail for 4% and 1%, respectively, of the period 13–24 March (wind speeds >8 m s⁻¹ and temperatures <0°C). We assume that wind speeds measured at the Kriegerhorn lower than 8 ms⁻¹ do not contribute significantly to the redistribution of snow at the Mohnensattel, so only events with wind speeds greater than 8 ms⁻¹ are considered. (The influence of wind speed on the amount of drifting snow is discussed in detail in section 6.1.) We also suppose that at temperatures exceeding the freezing point, snow erosion is suppressed by the exponentially increased cohesion force between snow grains (cf. Equation (11)). For the snowdrift simulation, we identified a typical westerly and northeasterly wind pattern, henceforth referred to as W₁ (Fig. 3a) and NE (Fig. 4a). The precipitation rate for the NE wind situation could be calculated from precipitation measurements as

(39)

which is equivalent to an increase in the snow height of 0.25 m over windless conditions. Thus, precipitation contributes considerably to the snow distribution within this time interval. Substituting Φ_pre into Equation (38) gives

(40)

We defined an additional westerly storm event, W₂ (Fig. 3b), for further parameter studies. Following Schneiderbauer and Pirker (2010) the wind speed, wind directions and temperature at the spatial Dirichlet-type boundary conditions are deduced by a mass-conserving optimization approach from the numerical weather prediction model ALADIN–Austria for all three individual wind situations (W₁, W₂ and NE). The wind speeds and wind directions at the Kriegerhorn for these specific wind situations are given in Table 1. Initial conditions for the flow and temperature distribution within the snowdrift simulation are taken from the converged boundary conditions analysis. Integration times for the initial and boundary conditions simulation are set to in order to obtain fully developed flow fields (Schneiderbauer and Pirker, 2010).

Fig. 1. The area around the Mohnensattel. The solid rectangle indicates the computational domain for the snowdrift simulation, the dark gray arrow shows the location of the Kriegerhorn station and the light gray arrow indicates north. The redistribution of snow is evaluated within the extent of the dashed rectangle. The color bar indicates the elevation in meters; spatial coordinates are in meters; black isolines correspond to Δz = 10 m.

Fig. 2. Relative frequencies (%) (a) for the whole period and (b) for T < 0°C of the wind speeds (m s⁻¹) measured at the Kriegerhorn between 13 and 24 March 2007.

The appropriate definition of the turbulent boundary conditions deeply impacts the accurate prediction of the turbulent diffusion in Equation (3). Although the turbulent viscosity, μ _t, approximately equals the molecular viscosity in the free stream region, μ _t is in the atmospheric boundary layer (which is in alpine terrain) leading to intense resuspension. Following Schneiderbauer and Pirker (2010; and references therein) atmospheric boundary profiles are applied at the spatial boundaries.

The lower boundary at the snow cover is assumed to be a rough wall with a roughness height given by Equation (30). It should be noted that the roughness height in real terrain is not influenced by drift, since the roughness height predicted by Equation (30) is generally much smaller than the terrain roughness (Doorschot and others, 2004), which is in our case. However, in this paper we assume that the terrain roughness is sufficiently resolved bythe numerical grid, and this, in turn, implies that the application of Equation (30) at the bottom boundary is valid. Furthermore, in areas where , h ₀ strongly exceeds the terrain roughness, . Finally, at the top boundary a zero-gradient boundary condition is applied.

5.3. Numerical discretization and grid

For the discretization of the transport equations (3) and (A7) a second-order upwind scheme is used. The derivatives appearing in the diffusion terms in Equations (3) and (35) are computed by central differencing, and the pressure–velocity coupling is achieved by the SIMPLEC algorithm (Van Doormal and Raithby, 1984), whereas the face pressures are computed as the average of the pressure values in the adjacent cells (linear interpolation).

We use a hexahedral finite-volume mesh. The horizontal extensions of the grid are 1000 m in the west–east direction and 950 m in the north–south direction. The top boundary is placed 1000 m above the mountain top. The minimal horizontal resolution is 2 m around deposition zones downwind of the ridge, and is linearly expanded by 5% towards the boundaries. The heights of the vertices at the surface level are bilinearly interpolated from a 5 m resolved DEM dataset. The first cell layer above the surface level is of constant thickness ∼1 m to meet the h ⁺ conditions required by the law-of-thewall (Equation (28)). It has been shown that this is sufficient to obtain acceptable results for the turbulence quantities near the surface (Kim and Patel, 2000; Schneiderbauer and Pirker, 2010). The vertical stretching from the surface to the top of the grid is set to 10%. The total number of gridcells is 106 × 103 × 30.

6. Sensitivity Studies

Prior to investigating the absolute snow distribution on 24 March 2007 and the redistribution of snow between 13 and 24 March 2007, we describe the impact of wind speed and the model dependency on the grid resolution. In both studies, the influence of time-dependent change in the topography was not considered. Its impact on the model results is shown at the end of this section. The following parametrization is used for these analyses: ρ _p = 917 kg m⁻³, d _p = 300 μm, C _D ≈ 0.4 (assuming spherical particles), h _SD,0 = 2 m, S = 25, Δt = 0.5 s and Δt’ = 10⁻³ s.

6.1. How does wind speed affect the redistribution of snow?

The near-ground wind fields for both westerly wind situations, W₁ and W₂, are shown in Figure 3. It can be clearly seen that large speed-up ratios appear due to the presence of the ridge in both cases. Furthermore, a southerly wind develops downwind of the ridge, causing a redistribution of snow to the stagnation area formed by the cliffy terrain at the northern boundary of the domain (200/150) (the first coordinate corresponds to the west–east direction and the second to the south–north direction, both in meters). Figure 4b illustrates the ratio between the two westerly wind situations. While the wind speed is nearly double at the ridge compared to , the velocity of the southerly wind downwind of the ridge is approximately triple. This nonlinearity in the wind field may lead to significantly increased redistribution of snow in some leeward areas. The ratio between the wind situations is ∼1.1 at the Kriegerhorn station (Table 1). The corresponding snow distributions and , with h _SD,0 = 2 m after a t = 2 hour drifting period, are shown in Figure 5. It can be seen by comparing the final snow depths that the increased wind speed in the W₂ case leads to four times more erosion than in the W₁ case upwind of the ridge (see Fig. 8a). Similarly, in the stagnation area near the northeastern cliffy terrain (at (200/150), Fig. 8a), up to nine times increased accumulation can be observed, while is only three times in the upwind area. Equations (9) and (14), which give the mass sources for aerodynamic entrainment, , and particle ejections, , support the above relationship between wind speed and erosion rate:

(41)

Thus, particle ejections can be classified as the dominating erosion mode in active saltation since a doubling of the wind speed causes approximately a quadrupling of the ejection rate. Furthermore, a doubling of the wind speed is equivalent to an approximately four times increased airborne shear stress, which makes it possible to keep four times more particles in saltation ( and Equation (26)). If mass exchange between saltation and suspension is neglected, the volume fraction within saltation can be expressed simply as . By reusing the above argument , an estimation for the saltation mass flux, Φ_s (kg m⁻² s⁻¹), computed by SnowDrift3D and integrated over the depth of the saltation layer, D, is given by

(42)

which agrees with the known dependency of the integrated saltation mass flux on (Clifton and Lehning, 2008). Equation (42) gives additional justification for the simple approximation for the particle velocity, u _p (Equation (1)). Strictly speaking, the suspension mass flux should have been included in the above estimate, since the snowdrift patterns shown in Figure 5 are a result of both transport modes. Additional evidence for the above statement is given by the analytical solution of Equation (3) in case of equilibrium suspension (e.g. Budd, 1966; Bintanja, 2000):

(43)

where it is assumed that the reference height, h _c, approximately equals the height of the saltation layer, h _s. In this case the suspension mass flux is

(44)

As h → hs in Equation (43), i.e. when it tends towards the limit, the saltation volume fraction, α _s, is approached, which is of the order of . This implies that ) approaches and this, in turn, supports Equation (42). Now, let us assume that h > h _s. If u_∗ < u_{∗ 0}, where u_{∗ 0} is a function of h, strongly exceeds the cubed dependence on u_∗ ; otherwise since slowly approaches 1 as u_∗ → ∞. Our results additionally support that directly above the saltation layer , with e > 3 locally exceeding numerical values of e ≈ 4. These additionally suggest that as h → ∞, i.e. where the suspension system is negligibly influenced by saltation and corresponds to larger-scale redistribution, e → 1, as indicated by Lehning and others (2008) and Dadic and others (2010) for large-scale transport. However, since ) exponentially decreases with increasing h for fixed u_∗ (Fig. 6), suspension contributes subsidiarily to the overall snow transport and, hence, the dependence of on u_∗ is assumed to be peripheral and saltation can be assumed to be the predominant transport mode. Finally, Figure 6 illustrates that the numerical solution of the transport equation (3) suitably matches the analytical solution (Equation (43)). However, at ∼2h _c the volume fraction is over-predicted by the simulation, which can be explained by a distorted logarithmic wind profile due to the presence of the hill. Figure 6 also shows that the diffusion coefficient proposed in Equation (4) fits the requirements for the simulation of blowing snow. In summary, we conclude that the amount of redistributed snow is and the predominant saltation mass flux is .

Fig. 3. Near-ground wind speeds (m s⁻¹) and wind directions around the Mohnensattel at t = 2 hours for two typical westerly wind situations, (a) W₁ and (b) W₂. The spatial coordinates are in meters and the black isolines correspond to Δz = 4 m.

Fig. 4. (a) Near-ground wind speeds (m s⁻¹) and wind directions around the Mohnensattel at t = 2 hours for the typical northeastern wind situation, NE. (b) Ratio between the two westerly wind situations, computed by . The spatial coordinates are in meters and the black isolines correspond to Δz = 4 m.

Fig. 5. Snowdrift patterns around the Mohnensattel at t = 2 hours for the westerly wind situations (a) W₁ and (b) W₂. The color bar indicates the snow depth, h _SD/h _SD,0 − 1, the spatial coordinates are in meters and the black isolines correspond to Δz = 8 m.

Fig. 6. Comparison of vertical profiles of the volume fraction of snow grains, α. Symbols × and ■ show simulated profiles at wind situation W₂ at two different locations upwind of the ridge with τ _a = 3 Pa. The solid curve corresponds to the analytical solution (Equation (43)) of Equation (3) for equilibrium suspension (Budd, 1966; Bintanja, 2000).

6.2. How does the grid resolution influence the model results?

The choice of grid resolution is a compromise between the spatial dimensions of the area of interest, the resolution of the DEM, the numerical premises and computational resources. It is important to have an adequate grid resolution to maintain the desired terrain features resolved within the DEM. The numerical grid discussed in section 5.3 meets the condition of conserving the DEM data downwind of the ridge, but the number of gridcells was reduced in areas that were not of specific interest (e.g. towards the spatial boundaries).

In order to evaluate the sensitivity of the solution to the spatial discretization, a second grid with decreased resolution (referred to as the coarse grid) was generated. The maximal horizontal resolution is 4 m and the growth rates are set the same as for the fine grid. This gives a total number of gridcells of 80 × 78 × 30 and a resolution generally less than that of the DEM.

The snowdrift pattern for a t = 2 hours drifting period with h _SD,0 = 2 m s⁻¹ for wind situation W₂ is plotted in Figure 7b. A difference plot, i.e. , comparing the results from the [1] = coarse and [2] = fine grids is shown in Figure 8c. Overall, the final snowdrift pattern obtained using the coarse grid was similar to that using the fine grid (Fig. 5b); however, as a result of the decreased resolution of the coarse grid, the terrain edges in northern (200/150) and northeastern directions and the minor depressions upwind (−50/0) and downwind (100/50) of the ridge are less well formed. Mott and Lehning (2010) made analog studies for Alpine3D, and results suggested that less distinct elevation leads to decreased speed-up ratios and therefore to less erosion. In other words, less redistribution of windward snow to the lee of the ridge is observed. Furthermore, as found by Mott and Lehning (2010), less variability of the snow depth is retained using the coarse grid. Although the snow cornice at the ridge is well formed at both resolutions, the absolute snow height at the ridge cornice decreases with increasing grid spacing, which is also supported by the results of Mott and Lehning (2010).

Fig. 7. Snowdrift patterns (a) using the ALE method with a fine grid and (b) using a coarse grid without applying the ALE method, around the Mohnensattel at t = 2 hours for the westerly wind situation, W₂. The color bar indicates the snow depth h _SD/h _SD,0 − 1 (h _SD,₀ = 2 m), the spatial coordinates are in meters and the black isolines correspond to Δz = 8 m.

Fig. 8. Difference plots, i.e. , for the snowdrift patterns in the test area at t = 2 hours (a) for the two westerly wind situations, [1] = [W₁] and [2] = [W₂], (b) for the activated ([2] = ALE) and deactivated ALE approach and (c) for the [1] = coarse and [2] = fine grids. The spatial coordinates are in meters, and the black isolines correspond to Δz = 8 m.

In conclusion, the simulation on the coarse grid was able to reproduce the typical snowdrift pattern, but a decreased accuracy and variability of snow heights was observed. The required computational time (including the wind-field computation) using both CPUs of a personal computer with an AMD Athlon 64 X2 Dual 2.2 GHz processor was 71 min for the fine grid and 35 min for the coarse grid.

6.3. How does the time-dependent change in topography influence the model results?

Given the considerable computing times required by SnowDrift3D, reducing the number of equations to be solved is desirable. The time-dependent change in the topography of the snow cover could be omitted, as done in the previous section. However, snow cornices up to 10 m high are formed frequently at the ridge at this site, in which case the above simplification would be invalid. To quantify the error made by such an omission, we compare the snowdrift patterns after a t = 2 hours period at wind situation W2 with and without the topographical adaptions of section 4.3.

The final snowdrift pattern created by applying the time-dependent topography changes is shown in Figure 7, and the corresponding snowdrift pattern for the steady topography is illustrated in Figure 5b. Visually comparing these figures, one observes that the growing snow cover at the ridge leads to a downwind shift of the snow cornice, which is also indicated in the normalized difference plot in Figure 8b. The difference in the snow depth at the ridge (Fig. 8b) can be explained similarly by the propagation of the snow cornice. As a result, the downwind wind field inevitably changes, causing an additional minor modification of the downwind snowdrift pattern. From Figure 8b it can also be seen that snowdrift causes a smoothing of the terrain: depressions and chutes are filled and snow is ablated at ridges. In this simulation it led to less snow deposition in the depressions directly upwind (-50/0) and downwind (100/50) of the ridge. Further, less accumulation due to topographical smoothing at the terrain edge at the northeastern stagnation area (200/150) was also observed. In conclusion, excluding the time-dependent changes in the topography should create negligible errors for minor changes in the snow depth due to erosion and sedimentation (0(<1) m); however, larger deviations due to the growth and reduction of the snow cover should be considered.

7. Comparison with TLS

In this section we present a comparison of simulated snowdrift patterns with TLS of actual snowdrift events (sections 5.1 and 5.2). The same parameterization was used as in the sensitivity runs: ρp = 917 kg m⁻³, dp = 300 μm, C _D ≈ 0.4 (assuming spherical particles), h _SD,0 = 2 m, S = 25, Δt = 0.5 s and Δt’ = 10⁻³ s.

7.1. Snow distribution on 24 March 2007

The first step was to adequately reproduce the snowdrift pattern measured on 24 March 2007. This was primarily affected by westerly winds. Absolute values of measured and modeled snow depths were not compared, as the final snowdrift pattern is a linear combination of two westerly wind events, W1 and W2, instead of a reconstruction of the winds appearing over the whole snow season. It was assumed that the duration of both individual wind events was ∼8 hours.

The simulated snow heights produced when (1) excluding and (2) including the time-dependent changes in topography are shown in Figures 9a and 10a, respectively. Based on the outcomes of the sensitivity study in section 6.1, it is appropriate to conclude that the final snow patterns plotted in Figures 9a and 10a are primarily formed by the storm event W2. Similarly, as concluded in section 6.3, the snow cornice at the ridge is shifted downwind when additionally solving Equations (34) and (35). Surprisingly, even for these high snow depths, both simulations yielded comparable snow distributions (Fig. 10b).

Fig. 9. (a) Computed snowdrift pattern for a linear combination of W₁ including precipitation and W₂. (b) Measured absolute snow heights on 24 March 2007 (color bars in meters). The spatial coordinates are in meters, the black isolines correspond to Δz = 4.5 m and the white lines indicate the confidence region of the measurement.

Fig. 10. (a) Computed snowdrift pattern for a linear combination of W₁ including precipitation and W₂ including changing topography (the black isolines correspond to Δz = 4.5 m). (b) Differences between activated ([2] = ALE) and deactivated ALE approach computed by . The spatial coordinates are in meters.

The absolute snow heights measured by TLS in the test area on 24 March 2007 are shown in Figure 9b. Snow depths up to 8 m can be observed at the ridges, which is also given by the simulation. Equally important, the downwind propagation of the snow cornice at (0/0) seen in the measurement is also produced by the modeled results. Another large deposition area was identified by both methods at the northern terrain edge at (200/150).

As discussed in section 6.3, snowdrift leads to terrain smoothing and, as a result, less snow is deposited in terrain sinks if the time-dependent change in topography is included. This was especially true downwind of the ridge where an intense southerly wind was present at W₁ and W₂. Various small, well-defined areas of snow deposits were observable in the measurements and the numerical results (e.g. downwind of the ridge at (100/75) and upwind of the ridge near the steep terrain at (−100/200)).

In conclusion, the snowdrift patterns resulting from the numerical simulation are in close agreement with the measurement results. A comparison of the absolute snow heights was not possible, as we did not account for the entire snow season leading up to 24 March 2007.

7.2. Snowdrift and precipitation between 13 and 24 March 2007

Here we consider a drift event with additional precipitation between 13 and 24 March 2007. Similar investigations were performed by Mott and others (2010) in the Wannengrat area with the Alpine3D model. The wind data for this site (Fig. 2) indicate that northeasterly (not only westerly) winds contribute significantly to the redistribution of snow during the defined time period. A representative northeasterly wind load case was defined (as in section 5.2 and Fig. 4a). At the ridge, the winds shift from northeasterly to easterly, and windless or backflow regions are present downwind of the ridge. The integration time, with S = 25, was 350s for the NE wind situation and 1200s for the W₁ wind situation. (For a description of the relative frequencies of these wind conditions, refer to section 5.2 and Fig. 2b.)

The snow redistribution patterns resulting from the numerical simulation for the given time period are shown in Figure 11a. The corresponding measurement data are given in Figure 11b, and the differences between the simulation and measurement results in Figure 12. Upon qualitative inspection, it seems that SnowDrift3D was able to adequately capture the typical deposition patterns, as seen for example in (1) the widespread deposit at (−50/225), (2) the accumulation in the NE stagnation area at the terrain edge, (200/150), and (3) below the steep terrain at (100/200). The well-defined depositional area at (100/75) that was a result of the westerly wind event was also reproduced by the model here. The model similarly reproduced the shift of the cornice easterly at (50/0) and the back-distribution of snow at the ridge to the west as a consequence of the speed-up seen in the easterly winds. The numerical results, however, overestimated the snow cornice formed by the westerly winds at (25/100) (Fig. 12), which may be explained by the uncertainty in the amount of erodible snow upwind of the ridge.

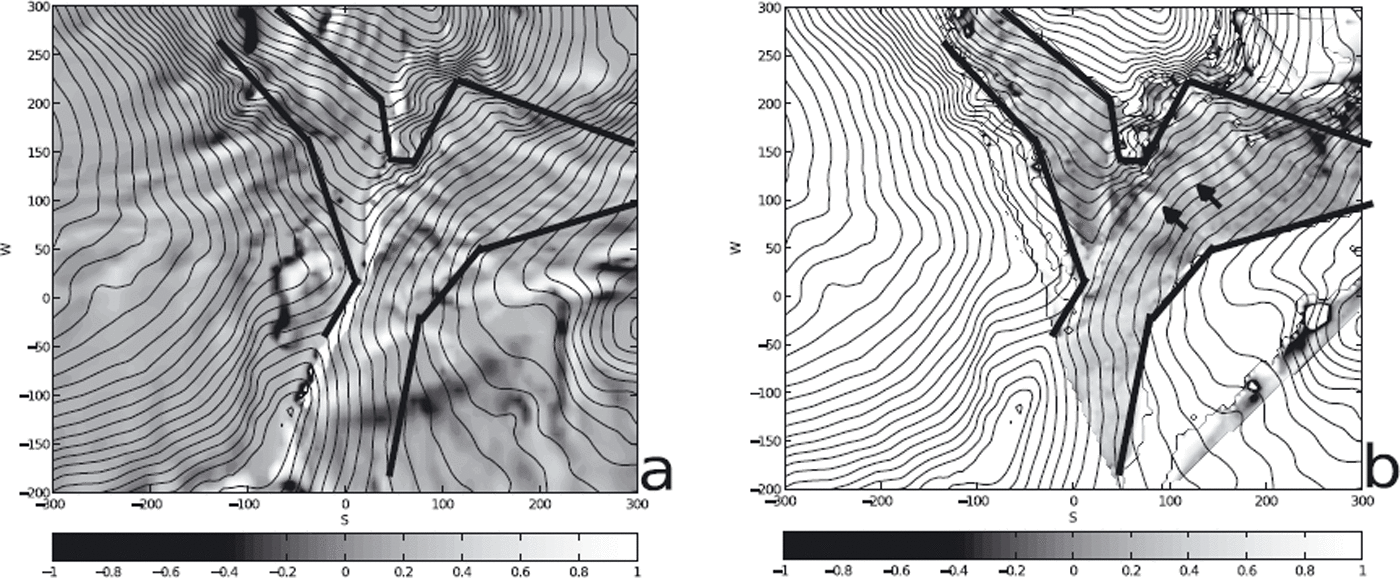
Fig. 11. Redistribution of snow between 13 and 24 March 2007 (color bars in meters): (a) computed and (b) measured by TLS. The spatial coordinates are in meters, the black isolines correspond to Δz = 8 m, the thick black lines display the confidence region of the measurement and the black arrows indicate snowslides. Both patterns were interpolated to a 5 m grid for better comparability.

Fig. 12. Differences in meters of [2] = modeled and [1] = measured changes in snow depth, i.e. , for the redistribution of snow between 13 and 24 March 2007 (Δz = 5 m). The thick black lines display the confidence region of the measurement, the spatial coordinates are in meters and the black arrows indicate snowslides.

The absolute values of redistributed snow are in good agreement with measurements for the rest of the domain. Pearson’s linear correlation coefficient was calculated for the difference between the modeled and measured changes in snow depth for two areas – east of the ridge (x ∈ [20;100] and y ∈ [20; 90] (x denotes the spatial coordinate from west to east and y from south to north)) and near the steep terrain (x ∈ [100;160] and y ∈ [160;205]) – which resulted in values of R = 0.31 and R = 0.33, respectively. (To compute the correlation coefficients the measurement data were interpolated to the grid used for SnowDrift3D.) These values are less than those obtained by Mott and others (2010) who used Alpine3D to model two different snowdrift periods at three transects in the Wannengrat area. This may be explained by differences in the resolution of terrain features between the two grids: the numerical model uses a grid created from DEM data, which stem from airborne laser scan data, whereas the measurement data come from TLS. Certain terrain features may be shifted or not resolved by the numerical grid, leading to potential discrepancies with the measurement results. Furthermore, neglecting the time-dependent metamorphism within the snowpack, in particular snow settling, which is included in Alpine3D, inevitably leads to significant errors. (High positive temperatures frequently occurred over the investigated time period.)

The snowdrift pattern shown by the measurements at (150/125) (Fig. 11b and 12, arrows) was not reproduced by the numerical simulation. This is not a shortcoming of the model, but rather is due to an artificial release of the snowpack by blasting during routine avalanche control. The spatial variability in snow depth is considerably less in the numerical results in general, but this cannot be seen in the figures, as all snow heights were interpolated to a 5 m grid for better comparability. Overall, SnowDrift3D was able to capture the redistribution pattern appropriately.

8. Conclusions and Outlook

We have introduced the fine-scale atmospheric snowdrift model SnowDrift3D with a resolution of up to 2 m, which is primarily designed for the numerical modeling of single storm events.

We have presented detailed numerical studies showing the influence of the wind speed on the amount of redistributed snow. The model was able to reproduce the saltation mass flux to the expected scale of (Clifton and Lehning, 2008). The results also suggest that the suspension mass flux is of the order of , where e ≈ 4 directly above the saltation layer and where e → 3 with increasing height, h. This is reinforced by analytical solution of the diffusion equation (3) forthe case of equilibrium suspension. For a large-scale distribution, i.e. as h → ∞, the linear scaling of the suspension mass flux with wind suggested by Dadic and others (2010) is reproduced by SnowDrift3D.

It was deduced from sensitivity runs that for minor redistributions of snow , the time-dependent change in the topography of the snow cover can be neglected; however, this leads to an overestimation of snow heights within small depressions, due to smoothing of the terrain features.

A grid resolution sensitivity study has shown that using a grid spacing of the order of the resolution of the DEM data gives appropriate model results. Further decreasing the grid spacing does not significantly improve the model results.

The main simplification/limitation of the model presented here is the exclusion of the structural properties of the snowpack. Hence, the model is restricted to the application of single storm events. In order to model an entire snow season, the necessary improvements in terms of calculation efficiency can only be achieved by further gross simplifications. A second limitation of the current model is that sublimation of the saltation snow grains (Pomeroy and others, 1998; Neumann and others, 2009) is not considered. Future efforts will be invested to include a simple snowpack modeling as a next step.

The results of SnowDrift3D were validated by area-wide snow height measurements obtained by TLS. The simulated snowdrift patterns were in agreement with the measurement results for the two typical weather situations: dominant westerly winds on 24 March 2007 and prevailing northwesterly winds with precipitation over the period 13–24 March 2007. Both absolute snow heights and the redistribution predicted by the model are positively correlated with TLS measurements. However, correlations of simulated and measured changes in snow heights were less than those found by Mott and others (2010) using Alpine3D, since an appropriate modeling of the structural properties of the snowpack is missing in SnowDrift3D.

In conclusion, future modeling efforts need to concentrate on including a scheme for the structural properties of the snowpack, including snow metamorphism and the influence of additional particle properties on the fluid threshold. Furthermore, avalanche releases should be addressed, for example by using a Bingham constitutive law for the numerical modeling of the snowpack (Laaber, 2008). This would also improve the unrealistic overestimation of snow heights at cornices, by predicting breakage under weighting conditions. At this time the model results show, however, an appropriate quantitative measure of the amount of snow downwind and upwind of the ridge, which can provide additional important data to, for example, avalanche warning services.