Introduction
The basic concept of a weakened layer as the primary source of instability in the snow cover on a slope was used as an initial working hypothesis which determined the programme for the study of avalanche-formation conditions.
This paper presents a summary of investigations conducted at the field sites “Dukant” and “Chimgan” situated on the spurs of the western Tianshan, as well as at the site “Desna” near Moscow.
The high sensitivity of acoustic methods to changes in the structure of a material under deformation was a determining factor in the application of some of these methods to study snow-cover properties in an avalanche-prone zone. The aim of the work was to show the possible acoustic methods applicable in the remote recognition of avalanche-hazard situations. A method of acoustic emission measurement is used together with a method using a penetrometer equipped with a piezo-electric accelerometer. The paper by Reference Lawrence and BradleySt. Lawrence and Bradley (1977) demonstrated the relationship between acoustic emission through the snow cover and its stability on slopes. Sommerfeld (Reference Sommerfeld1977, 1982) and Reference GublerGubler (1980) found a correlation between low-frequency noise and snow-cover stability. Gubler used accelerometers inserted in the snow and demonstrated the starting time of natural avalanche activity. In contrast to Reference GublerGubler (1980), we used wide-range microphones installed in the starting zone of an avalanche. The time of avalanche hazard was determined by simultaneous measurements of acoustic emissions in the avalanche starting zone and of the mechanical characteristics of a specific weakened layer. The solution of this problem was preceded by laboratory tests on the mechanical properties of snow and formulation of a complex approach, that is, recording not only the amplitude and number of impulses but also the frequency characteristics of acoustic emission signals which are of some importance to the analysis. Let us first consider the various spectra of destruction.
Spectra of Destruction
Figure 1 shows the spectra of impact interaction between a sphere and a snow slab for energy values (1) 1.8 J, and (2) 2.6 J, and for an impact interaction energy of 5.2 J the emission is represented by three phases (3), (4), and (5). The abscissa represents a logarithmic scale of frequency and the ordinate is the emission amplitude. The amplitude increases and the frequency composition of the spectra changes with an increase in impact energy, namely, the spectra are likely to reflect the intensity of destruction processes in snow.

Fig. 1. The spectra of snow destruction.
The emission-intensity maxima are observed in the ranges of: I, 4–8 kHz; II, 2–2.5 kHz; III, 250–500 Hz, and IV, 25 Hz. Using model representations of harmonic oscillations (Reference Voronina and YepifanovVoronina and Yepifanov, 1980) and considering the real sizes of the structural elements of snow, we car assess the degree of destruction corresponding to each of these four ranges. For example, the effective radius R e = 1.4 mm corresponds to the first high-frequency range, 4–8 kHz. This radius is the mean size of a neck. It can be determined that there are other degrees of destruction: II, crystallite destruction; III, collapse of the grain aggregates as structural formations; the IVth level refers to the process of dynamic interaction between the debris of structural formations. In the future, we proposed to use information on different scales of snow destruction to study processes preceding avalanche release.
Having related the characteristics of acoustic emission to the destruction of the elements of snow structure, we obtained a perspective method for remote determination of the process in the starting zone of avalanche formation; it is necessary to define the mechanical properties of the snow cover and to measure the processes of snow destruction separately from signals of acoustic emission.
Results of Dynamic Tests
The mechanical properties of snow were determined using a penetrometer with a piezo-electric accelerometer (Reference Yepifanov and KudryaYepifanov and Kudrya, 1985). Such penetrometers allow us to measure snow characteristics at any moment during collision. They were first used in ice tests (Yepifanov, 1985Reference Yepifanov[a], [b]). Optimum masses and sizes of penetrometers, and initial collision velocities, were determined experimentally for various snow-cover conditions. Snow properties were assessed both in the vertical and horizontal directions.
The following equation is accepted as the initial case for stopping a free-falling rigid penetrometer:
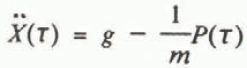
where P is the response of snow, τ is time, X is the depth of penetration, m is the mass of the penetrometer, and g is gravitational acceleration.
The voltage produced by a piezo-electric accelerometer is proportional to the force applied to the piezo-element; hence, to the penetrometer acceleration:

where n is the coefficient of transformation of the measuring system; U is the voltage; C, R are the capacity and electrical resistance of the measuring line, respectively τ0 = RC.
Figure 2 shows the dependence of the force P, N (response of the snow) and mean stress at the sphere/snow interface σ (MPa) (dashed line) on the depth of a sphere’s penetration into the snow X × 10−3 m; a smoothed oscillogram of impact interaction U (mV) and the time of collision τ (ms) is also shown here.
The shape of the oscillogram and also the functions P(X) and σ(X) are determined by the collision process prevailing at a particular stage: (1) elastic deformation of grains and necks; (2) neck destruction; (3) elastic compression of air in pores; (4) viscous transport of grains, or (5) their collapse and densification. During stage 1, from the beginning of collision until the first extreme, which corresponds to brittle fracture, that is, snow hardness σT, the initial structure would not change considerably and the penetration of a sphere into snow is due to elastic deformation. In our experiment σT = 0.11 MPa.
The effective modulus E = δσ/δХ for stages 1–4 of the relation equals E 1 = 25 × 108 Pa, E 2 = 2.9 × 108Pa, E 3 = 3 × 106Pa, and E 4 = 20 × 108Pa, respectively; viscosity coefficients η 1 = 25, η 2 = 41, η 3 = 73, and η 4 = 209 Pa s. Time of relaxation is assessed by the relation τ= 1/ω = η 3 /E 3 = 2.4 × 10 −5 s, and does not contradict the ice-relaxation time characterizing the elasticity of ice. Since ω = 1/τ = 2πf, the signals of acoustic emission may be expected to have a frequency of f = 6 kHz during snow destruction. This fact has been confirmed experimentally and allows us to consider the computed values of E and η to be close to the real ones.

Fig. 2. A graph of impact-interaction loading.
Thus, the penetration of a sphere into snow leads to the destruction of the initial snow structure and to the formation of a layer consisting of separate crystallites and their debris which, in turn, densifies. It has been shown that the mechanical properties of an undisturbed layer differ considerably from those of the densified snow. That is why, in order to define the characteristics of the undisturbed snow structure, we have considered only that part of the impact interaction process which precedes the collapse of the initial structure.
If we take the volume of a hole as an indicator of the degree of destruction and the energy losses in the first stage of a collision for the energy losses (defined by the P(X) relationship), then the specific energy of destruction is ε = 6.6 × 104 J/m3.
The true degree of destruction may be defined by changes in the mechanical properties of snow, e.g. hardness: greater compression corresponds to higher compaction, hence the greater hardness.
Figure 3 shows the dependence (1) of the σ/σ0 ratio on time τ (min). Hardness σ along the track centre and hardness σ0 of the undisturbed upper layer of snow cover were defined just after and during 1.5 h passage of a caterpillar-tracked vehicle, Buran. After passage of the vehicle hardness of the snow increased, approaching the threshold value. Over 45 min, hardness of the compacted layer became about an order of magnitude higher than it was initially. Relaxation time τ2 = 1.5 × 103 s is defined by the formula σ/σ0 ∼ f(τ). This value characterizes the process of snow regaining, after passage of a vehicle, a new quasi-equilibrium state, i.e. plasticity.
The relationship σ/σ∞ ∼ f(z) (Fig. 3, curve 3) gives us some idea about the course of hardness variation with snow depth Z (cm) 90 min. after the passage of Buran, hence about distribution of maximum stresses in the volume. Here, σ∞ is the hardness of a layer, where we failed to demonstrate a difference between the measured values before and after vehicle impact. In order to estimate the hardness of every stratum in a snow layer, we have applied the method of making measurements in a pit. It appeared that the “compaction” cone did not reach the ground surface. Even at a depth of 10–15 cm, it is difficult to observe after effects. So, it is quite simple to evaluate the true degree of destruction.

Fig. 3. Variations in snow properlies after the passage of a vehicle.
Snow density ρ as a function of depth Z was estimated at the same time as measuring its hardness. Curve 2 shows the same tendency to decrease as curve 3, but hardness characterizes the mechancial properties of snow in a different way. Maximum hardness ρ/ρ0 = 2 occurs at the surface of contact.
An average specific stress under a caterpillar-tracked Buran is calculated by the formula P 1 = K 4 (M 1/S 1) when K 4 = 2, which is well known in mechanics. In our case, the coefficient of proportionality in Gerstner’s law is C 1 = P 1/X = 4 × 103 Pa/m when snow settling is X = 0.15 m. Knowing the shape of the relationship σ/ σ∞ ∼ f(Z), which defines the stress in any layer normal to its axis, and having assumed that σT ∼ P 1, we can describe the snow behaviour under load (Reference Ishlinskiy and Kondrati'yevaIshlinskiy and Kondrati'yeva, 1950).
Hence, acoustic emission methods make it possible to assess the mechanical characteristics of snow and reveal the specific weakened stratum, as well as monitoring the processes in the snow cover for the determination of avalanche-formation conditions.
Forecasting Avalanche Hazard
We use the value K = C/P as a criterion of avalanche hazard where P is snow loading on a layer, and C is the hardness or cohesion between particles in a weakened layer. This criterion has no specific advantages but in practice some scientists use it.
Figure 4 shows the dependence (1) of the stability parameter K, and (2) the acoustic frequency range, etc. on time τ (24 h) for that section of the snow cover in the starting zone of any given avalanche-prone area which represents an erosion cone on the slopes of Mazardgan mountain (on the spurs of the Tianshan mountains). The mean angle of slope is 32–38°, and the exposure is from north to east-south-east. The slopes are covered by grass and sparse bushes; areas adjacent to the watershed lines are rocky.

Fig. 4. Variation of the stability parameter K and acoustic activity ΣΑ in time (24 h) for avalanche-hazard slopes.
When K = 0.5, the state of the snow cover on a slope is considered as an avalanche hazard. Difficulty in making pit measurements has compelled us to search for a remote-sensing method for estimating snow-cover stability, e.g. using acoustic emission signals.
Intensification of the average activity of specific signals corresponds to a decrease in snow-cover stability. When the stability parameter has constant values or increasing ones, the intensity of acoustic emission decreases, reaching the background level; this is not in contradiction to the results of Reference Lawrence and BradleySt. Lawrence and Bradley (1977), Sommerfeld (Reference Sommerfeld1977, 1982), and Reference GublerGubler (1980).
The correlation found by considering the results of spectral analysis can be used to determine the stability of the snow cover on slopes; hence, we can foresee a way of using a remote-sensing method for monitoring avalanche hazard.
Conclusion
Thus, we have attempted to show there are good prospects for the use of acoustic emission methods in the study of a snow cover under stress and strain, and in forecasting the avalanche hazard. In particular, the process of snow destruction under conditions of compaction in various ways is investigated. The stages of destruction have been defined and the mechanical properties corresponding to these stages have been determined. We have assessed the distribution of stresses in the snow cover after passage of a caterpillar-tracked vehicle. The correlation between acoustic emission and the stability parameter of the snow cover on a slope has also been found.






