A numerical study of fully nonlinear waves propagating through a two-dimensional deep fluid covered by a floating flexible plate is presented. The nonlinear model proposed by Toland (Arch. Rat. Mech. Anal., vol. 289, 2008, pp. 325–362) is used to formulate the pressure exerted by the thin elastic sheet. The symmetric solitary waves previously found by Guyenne & Părău (J. Fluid Mech., vol. 713, 2012, pp. 307–329) and Wang et al. (IMA J. Appl. Maths, vol. 78, 2013, pp. 750–761) are briefly reviewed. A new class of hydroelastic solitary waves which are non-symmetric in the direction of wave propagation is then computed. These asymmetric solitary waves have a multi-packet structure and appear via spontaneous symmetry-breaking bifurcations. We study in detail the stability properties of both symmetric and asymmetric solitary waves subject to longitudinal perturbations. Some moderate-amplitude symmetric solitary waves are found to be stable. A series of numerical experiments are performed to show the non-elastic behaviour of two interacting stable solitary waves. The large response generated by a localised steady pressure distribution moving at a speed slightly below the minimum of the phase speed (called the transcritical regime in the literature) is also examined. The direct numerical simulation of the fully nonlinear equations with a single load reveals that in this range the generated waves are of finite amplitude. This includes a perturbed depression solitary wave, which is qualitatively similar to the large response observed in experiments. The excitations of stable elevation solitary waves are achieved by applying multiple loads moving with a speed in the transcritical regime.

In this paper we investigate the possibility of fast waves affecting the evolution of slow balanced dynamics in the regime $Ro\sim Fr\ll 1$ of a rotating shallow water system, where $Ro$ and $Fr$ are the Rossby and Froude numbers respectively. The problem is set up as an initial value problem with unbalanced initial data. The method of multiple time scale asymptotic analysis is used to derive an evolution equation for the slow dynamics that holds for $t\lesssim 1/(fRo^{2})$, $f$ being the inertial frequency. This slow evolution equation is affected by the fast waves and thus does not form a closed system. Furthermore, it is shown that energy and enstrophy exchange can take place between the slow and fast dynamics. As a consequence, the quasi-geostrophic ideology of describing the slow dynamics of the balanced flow without any information on the fast modes breaks down. Further analysis is carried out in a doubly periodic domain for a few geostrophic and wave modes. A simple set of slowly evolving amplitude equations is then derived using resonant wave interaction theory to demonstrate that significant wave-balanced flow interactions can take place in the long-time limit. In this reduced system consisting of two geostrophic modes and two wave modes, the presence of waves considerably affects the interactions between the geostrophic modes, the waves acting as a catalyst in promoting energetic interactions among geostrophic modes.

Wall shear stress measurements employing a hot-film sensor along with laser Doppler velocimetry measurements of the axial and tangential velocity and turbulence profiles in a pulsating turbulent pipe flow are presented. Time-mean and phase-averaged results are derived from measurements performed at pulsation frequencies ${\it\omega}^{+}={\it\omega}{\it\nu}/\bar{u}_{{\it\tau}}^{2}$ over the range of 0.003–0.03, covering the low-frequency, intermediate and quasi-laminar regimes. In addition to the base case of a single pulsation imposed on the mean flow, the study also investigates the flow response when two pulsations are superimposed simultaneously. The measurements from the base case show that, when the pulsation belongs to the quasi-laminar regime, the oscillating flow tends towards a laminar state in which the velocity approaches the purely viscous Stokes solution with a low level of turbulence. For ${\it\omega}^{+}<0.006$, the oscillating flow is turbulent and exhibits a region with a logarithmic velocity distribution and a collapse of the turbulence intensities, similar to the time-averaged counterparts. In the low-frequency regime, the oscillating wall shear stress is shown to be directly proportional to the Stokes length normalized in wall units $l_{s}^{+}~(=\sqrt{2/{\it\omega}^{+}})$, as predicted by quasi-steady theory. The base case measurements are used as a reference when evaluating the data from the double-frequency case and the oscillating quantities are shown to be close to superpositions from the base case. The previously established view that the time-averaged quantities are unaffected by the imposition of small-amplitude pulsed unsteadiness is shown to hold also when two pulsations are superposed on the mean flow.

This paper presents an experimental and theoretical investigation of high-Reynolds-number low-density reacting wakes near a hydrodynamic Hopf bifurcation. This configuration is applicable to the wake flows that are commonly used to stabilize flames in high-velocity flows. First, an experimental study is conducted to measure the limit-cycle oscillation of this reacting bluff-body wake. The experiment is repeated while independently varying the bluff-body lip velocity and the density ratio across the flame. In all cases, the wake exhibits a sinuous oscillation. Linear stability analysis is performed on the measured time-averaged velocity and density fields. In the first stage of this analysis, a local spatiotemporal stability analysis is performed on the measured time-averaged velocity and density fields. The stability analysis results are compared to the experimental measurement and demonstrate that the local stability analysis correctly captures the influence of the lip-velocity and density-ratio parameters on the sinuous mode. In the second stage of the analysis, the linear direct and adjoint global modes are estimated by combining the local results. The sensitivity of the eigenvalue to changes in intrinsic feedback mechanisms is found by combining the direct and adjoint global modes. This is referred to as the eigenvalue sensitivity throughout the paper for reasons of brevity. The predicted global mode frequency is consistently within 10 % of the measured value, and the linear global mode shape closely resembles the measured nonlinear oscillations. The adjoint global mode reveals that the oscillation is strongly sensitive to open-loop forcing in the shear layers. The eigenvalue sensitivity identifies a wavemaker in the recirculation zone of the wake. A parametric study shows that these regions change little when the density ratio and lip velocity change. In the third stage of the analysis, the stability analysis is repeated for the varicose hydrodynamic mode. Although not physically observed in this unforced flow, the varicose mode can lock into longitudinal acoustic waves and cause thermoacoustic oscillations to occur. The paper shows that the local stability analysis successfully predicts the global hydrodynamic stability characteristics of this flow and shows that experimental data can be post-processed with this method in order to identify the wavemaker regions and the regions that are most sensitive to external forcing, for example from acoustic waves.

In a fluidized bed, the drag force acts to oppose the downward force of gravity on a particle, and thus provides the main mechanism for fluidization. Drag models that are employed in large-scale simulations of fluidized beds are typically based on either fixed-particle beds or the sedimentation of particles in liquids. In low-Reynolds-number ($Re$) systems, these two types of fluidized beds represent the limits of high Stokes number ($St$) and low $St$, respectively. In this work, the fluid–particle drag behaviour of these two regimes is bridged by investigating the effect of $St$ on the drag force in low-$Re$ systems. This study is conducted using fully resolved lattice Boltzmann simulations of a system composed of fluid and monodisperse spherical particles. In these simulations, the particles are free to translate and rotate based on the effects of the surrounding fluid. Through this work, three distinct regimes in the characteristics of the fluid–particle drag force are observed: low, intermediate and high $St$. It is found that, in the low-$Re$ regime, a decrease in $St$ results in a reduction in the fluid–particle drag. Based on the simulation results, a new drag relation is proposed, which is, unlike previous models, dependent on $St$.

The inertial-subrange scaling of the axial velocity component is examined for the centreline of turbulent pipe flow for Reynolds numbers in the range $249\leqslant Re_{{\it\lambda}}\leqslant 986$. Estimates of the dissipation rate are made by both integration of the one-dimensional dissipation spectrum and the third-order moment of the structure function. In neither case does the non-dimensional dissipation rate asymptote to a constant; rather than decreasing, it increases indefinitely with Reynolds number. Complete similarity of the inertial range spectra is not evident: there is little support for the hypotheses of Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 32, 1941a, pp. 16–18; Dokl. Akad. Nauk SSSR, vol. 30, 1941b, pp. 301–305) and the effects of Reynolds number are not well represented by Kolmogorov’s ‘extended similarity hypothesis’ (J. Fluid Mech., vol. 13, 1962, pp. 82–85). The second-order moment of the structure function does not show a constant value, even when compensated by the extended similarity hypothesis. When corrected for the effects of finite Reynolds number, the third-order moments of the structure function accurately support the ‘four-fifths law’, but they do not show a clear plateau. In common with recent work in grid turbulence, non-equilibrium effects can be represented by a heuristic scaling that includes a global Reynolds number as well as a local one. It is likely that non-equilibrium effects appear to be particular to the nature of the boundary conditions. Here, the principal effects of the boundary conditions appear through finite turbulent transport at the pipe centreline, which constitutes a source or a sink at each wavenumber.

We study passive scalars in turbulent plane channels at computationally high Reynolds number, thus allowing us to observe previously unnoticed effects. The mean scalar profiles are found to obey a generalized logarithmic law which includes a linear correction term in the whole lower half-channel, and they follow a universal parabolic defect profile in the core region. This is consistent with recent findings regarding the mean velocity profiles in channel flow. The scalar variances also exhibit a near universal parabolic distribution in the core flow and hints of a sizeable log layer, unlike the velocity variances. The energy spectra highlight the formation of large scalar-bearing eddies with size proportional to the channel height which are caused by a local production excess over dissipation, and which are clearly visible in the flow visualizations. Close correspondence of the momentum and scalar eddies is observed, with the main difference being that the latter tend to form sharper gradients, which translates into higher scalar dissipation. Another notable Reynolds number effect is the decreased correlation of the passive scalar field with the vertical velocity field, which is traced to the reduced effectiveness of ejection events.

Sedimentation of a dispersed solid phase is widely encountered in applications and environmental flows, yet little is known about the behaviour of finite-size particles in homogeneous isotropic turbulence. To fill this gap, we perform direct numerical simulations of sedimentation in quiescent and turbulent environments using an immersed boundary method to account for the dispersed rigid spherical particles. The solid volume fractions considered are ${\it\phi}=0.5{-}1\,\%$, while the solid to fluid density ratio ${\it\rho}_{p}/{\it\rho}_{f}=1.02$. The particle radius is chosen to be approximately six Kolmogorov length scales. The results show that the mean settling velocity is lower in an already turbulent flow than in a quiescent fluid. The reductions with respect to a single particle in quiescent fluid are approximately 12 % and 14 % for the two volume fractions investigated. The probability density function of the particle velocity is almost Gaussian in a turbulent flow, whereas it displays large positive tails in quiescent fluid. These tails are associated with the intermittent fast sedimentation of particle pairs in drafting–kissing–tumbling motions. The particle lateral dispersion is higher in a turbulent flow, whereas the vertical one is, surprisingly, of comparable magnitude as a consequence of the highly intermittent behaviour observed in the quiescent fluid. Using the concept of mean relative velocity we estimate the mean drag coefficient from empirical formulae and show that non-stationary effects, related to vortex shedding, explain the increased reduction in mean settling velocity in a turbulent environment.

We present an experimental parametric study of spanwise centrifugal instabilities in an open cavity flow. We show that the mode selected at threshold depends on the cavity streamwise aspect ratio. For small aspect ratio, a steady mode is enhanced, while travelling waves are observed for large aspect ratio. The bifurcation is found to be supercritical for all configurations. Sidewall effects are shown to generate secondary flows that carry the vortical patterns. Spanwise confinement enhances the family of steady modes relative to the family of oscillatory modes. These results are discussed with respect to predictions from linear stability analyses and other flows developing centrifugal instabilities.

The acceleration of an inertial particle in a gas–solid flow arises from the particle’s interaction with the gas and from interparticle interactions such as collisions. Analytical treatments to derive a particle acceleration model are difficult outside the Stokes flow regime, but for moderate Reynolds numbers (based on the mean slip velocity between gas and particles) particle-resolved direct numerical simulation (PR-DNS) is a viable tool for model development. In this study, PR-DNS of freely-evolving gas–solid suspensions are performed using the particle-resolved uncontaminated-fluid reconcilable immersed-boundary method (PUReIBM) that has been extensively validated in previous studies. Analysis of the particle velocity variance (granular temperature) equation in statistically homogeneous gas–solid flow shows that a straightforward extension of a class of mean particle acceleration models (drag laws) to their corresponding instantaneous versions, by replacing the mean particle velocity with the instantaneous particle velocity, predicts a granular temperature that decays to zero, which is at variance with the steady particle granular temperature that is obtained from PR-DNS. Fluctuations in particle velocity and particle acceleration (and their correlation) are important because the particle acceleration–velocity covariance governs the evolution of the particle velocity variance (characterized by the particle granular temperature), which plays an important role in the prediction of the core annular structure in riser flows. The acceleration–velocity covariance arising from hydrodynamic forces can be decomposed into source and dissipation terms that appear in the granular temperature evolution equation, and these have already been quantified in the Stokes flow regime using a combination of kinetic theory closure and multipole expansion simulations. From PR-DNS data we show that the fluctuations in the particle acceleration that are aligned with fluctuations in the particle velocity give rise to a source term in the granular temperature evolution equation. This approach is used to quantify the hydrodynamic source and dissipation terms of granular temperature from PR-DNS results for freely-evolving gas–solid suspensions that are performed over a wide range of solid volume fraction ($0.1\leqslant {\it\phi}\leqslant 0.4$), Reynolds number based on the slip velocity between the solid and the fluid phase ($10\leqslant \mathit{Re}_{m}\leqslant 100$) and solid-to-fluid density ratio ($100\leqslant {\it\rho}_{p}/{\it\rho}_{f}\leqslant 2000$). The straightforward extension of drag law models does not give rise to any source in the granular temperature due to hydrodynamic effects. This motivates the development of better Lagrangian particle acceleration models that can be used in Lagrangian–Eulerian formulations of gas–solid flow. It is found that a Langevin equation for the increment in the particle velocity reproduces PR-DNS results for the stationary particle velocity autocorrelation in freely-evolving suspensions. Based on the data obtained from the simulations, the functional dependence of the Langevin model coefficients on solid volume fraction, Reynolds number and solid-to-fluid density ratio is obtained. This new Lagrangian particle acceleration model reproduces the correct steady granular temperature and can also be adapted to gas–solid flow computations using Eulerian moment equations.

Sinusoidal modifications to the leading edge of a foil, or tubercles, have been shown to improve aerodynamic performance under certain flow conditions. One of the mechanisms of performance enhancement is believed to be the generation of streamwise vortices, which improve the momentum exchange in the boundary layer. This experimental and numerical study investigates the formation and evolution of these streamwise vortices at a low Reynolds number of $Re=2230$, providing insight into both the averaged and time-dependent flow patterns. Furthermore, the strength of the vortices is quantified through calculation of the vorticity and circulation, and it is found that the circulation increases in the downstream direction. There is strong agreement between the experimental and numerical observations, and this allows close examination of the flow structure. The results demonstrate that the presence of strong pressure gradients near the leading edge gives rise to a significant surface flux of vorticity in this region. As soon as this vorticity is created, it is stretched, tilted and diffused in a highly three-dimensional manner. These processes lead to the generation of a pair of streamwise vortices between the tubercle peaks. A horseshoe-shaped separation zone is shown to initiate behind a tubercle trough, and this region of separation is bounded by a canopy of boundary-layer vorticity. Along the sides of this shear layer canopy, a continued influx of boundary-layer vorticity occurs, resulting in an increase in circulation of the primary streamwise vortices in the downstream direction. Flow visualisation and particle image velocimetry studies support these observations and demonstrate that the flow characteristics vary with time, particularly near the trailing edge and at a higher angle of attack. Numerical evaluation of the lift and drag coefficients reveals that, for this particular flow regime, the performance of a foil with tubercles is slightly better than that of an unmodified foil.

Within the framework of shallow-water magnetohydrodynamics, we investigate the linear instability of horizontal shear flows, influenced by an aligned magnetic field and stratification. Various classical instability results, such as Høiland’s growth-rate bound and Howard’s semi-circle theorem, are extended to this shallow-water system for quite general flow and field profiles. In the limit of long-wavelength disturbances, a generalisation of the asymptotic analysis of Drazin & Howard (J. Fluid Mech., vol. 14, 1962, pp. 257–283) is performed, establishing that flows can be distinguished as either shear layers or jets. These possess contrasting instabilities, which are shown to be analogous to those of certain piecewise-constant velocity profiles (the vortex sheet and the rectangular jet). In both cases it is found that the magnetic field and stratification (as measured by the Froude number) are generally each stabilising, but weak instabilities can be found at arbitrarily large Froude number. With this distinction between shear layers and jets in mind, the results are extended numerically to finite wavenumber for two particular flows: the hyperbolic-tangent shear layer and the Bickley jet. For the shear layer, the instability mechanism is interpreted in terms of counter-propagating Rossby waves, thereby allowing an explication of the stabilising effects of the magnetic field and stratification. For the jet, the competition between even and odd modes is discussed, together with the existence at large Froude number of multiple modes of instability.

The propagation of wave disturbances in water of uniform depth is discussed, accounting for both gravity and compressibility effects. In the linear theory, free-surface (gravity) waves are virtually decoupled from acoustic (compression) waves, because the speed of sound in water far exceeds the maximum phase speed of gravity waves. However, these two types of wave motion could exchange energy via resonant triad nonlinear interactions. This scenario is analysed for triads comprising a long-crested acoustic mode and two oppositely propagating subharmonic gravity waves. Owing to the disparity of the gravity and acoustic length scales, the interaction time scale is longer than that of a standard resonant triad, and the appropriate amplitude evolution equations, apart from the usual quadratic interaction terms, also involve certain cubic terms. Nevertheless, it is still possible for monochromatic wavetrains to form finely tuned triads, such that nearly all the energy initially in the gravity waves is transferred to the acoustic mode. This coupling mechanism, however, is far less effective for locally confined wavepackets.

When subject to sufficiently strong electric fields, particles and drops suspended in a weakly conducting liquid exhibit spontaneous rotary motion. This so-called Quincke rotation is a fascinating example of nonlinear symmetry-breaking phenomena. To illuminate the rotation of liquid drops we here analyse the asymptotic limit of large electric Reynolds numbers, $\mathit{Re}\gg 1$, within the framework of a two-dimensional Taylor–Melcher electrohydrodynamic model. A non-trivial dominant balance in this singular limit results in both the fluid velocity and surface-charge density scaling as $\mathit{Re}^{-1/2}$. The flow is governed by a self-contained nonlinear boundary-value problem that does not admit a continuous fore–aft symmetric solution, thus necessitating drop rotation. Furthermore, thermodynamic arguments reveal that a fore–aft asymmetric solution exists only when charge relaxation within the suspending liquid is faster than that in the drop. The flow problem possesses both mirror-image (with respect to the direction of the external field) and flow-reversal symmetries; it is transformed into a universal one, independent of the ratios of electric conductivities and dielectric permittivities in the respective drop phase and suspending liquid phase. The rescaled angular velocity is found to depend weakly upon the viscosity ratio. The corresponding numerical solutions of the exact equations indeed collapse at large $\mathit{Re}$ upon the asymptotically calculated universal solution.

We revisit, both numerically and analytically, the finite-time blowup of the infinite-energy solution of 3D Euler equations of stagnation-point type introduced by Gibbon et al. (Physica D, vol. 132, 1999, pp. 497–510). By employing the method of mapping to regular systems, presented by Bustamante (Physica D, vol. 240 (13), 2011, pp. 1092–1099) and extended to the symmetry-plane case by Mulungye et al. (J. Fluid Mech., vol. 771, 2015, pp. 468–502), we establish a curious property of this solution that was not observed in early studies: before but near singularity time, the blowup goes from a fast transient to a slower regime that is well resolved spectrally, even at mid-resolutions of 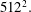$512^{2}.$ This late-time regime has an atypical spectrum: it is Gaussian rather than exponential in the wavenumbers. The analyticity-strip width decays to zero in a finite time, albeit so slowly that it remains well above the collocation-point scale for all simulation times 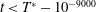$t<T^{\ast }-10^{-9000}$, where 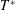$T^{\ast }$ is the singularity time. Reaching such a proximity to singularity time is not possible in the original temporal variable, because floating-point double precision (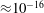${\approx}10^{-16}$) creates a ‘machine-epsilon’ barrier. Due to this limitation on the original independent variable, the mapped variables now provide an improved assessment of the relevant blowup quantities, crucially with acceptable accuracy at an unprecedented closeness to the singularity time: 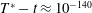$T^{\ast }-t\approx 10^{-140}$.