Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-20T01:24:29.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice Boltzmann simulations of low-Reynolds-number flow past fluidized spheres: effect of Stokes number on drag force

Published online by Cambridge University Press:  08 January 2016

Gregory J. Rubinstein ,
J. J. Derksen  and
Sankaran Sundaresan
Gregory J. Rubinstein
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08540, USA
J. J. Derksen
Affiliation:
Department of Chemical Engineering, Delft University of Technology, 2628 BL Delft, Netherlands
Sankaran Sundaresan*
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08540, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

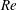In a fluidized bed, the drag force acts to oppose the downward force of gravity on a particle, and thus provides the main mechanism for fluidization. Drag models that are employed in large-scale simulations of fluidized beds are typically based on either fixed-particle beds or the sedimentation of particles in liquids. In low-Reynolds-number ($Re$) systems, these two types of fluidized beds represent the limits of high Stokes number (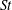$St$) and low 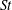$St$, respectively. In this work, the fluid–particle drag behaviour of these two regimes is bridged by investigating the effect of 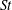$St$ on the drag force in low-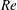$Re$ systems. This study is conducted using fully resolved lattice Boltzmann simulations of a system composed of fluid and monodisperse spherical particles. In these simulations, the particles are free to translate and rotate based on the effects of the surrounding fluid. Through this work, three distinct regimes in the characteristics of the fluid–particle drag force are observed: low, intermediate and high 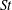$St$. It is found that, in the low-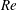$Re$ regime, a decrease in 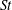$St$ results in a reduction in the fluid–particle drag. Based on the simulation results, a new drag relation is proposed, which is, unlike previous models, dependent on 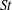$St$.

JFM classification

Multiphase and Particle-laden Flows: Fluidized beds Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 576 - 601
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K. & Clausen, J. R. 2010 Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42, 439–472.Google Scholar
Beetstra, R., van der Hoef, M. A. & Kuipers, J. A. M. 2007 Drag force of intermediate Reynolds number flow past mono- and bi-disperse arrays of spheres. AIChE J. 52 (2), 489–501.Google Scholar
Benzi, R., Succi, S. & Vergassola, M. 1992 The lattice Boltzmann equation: theory and applications. Phys. Rep. 222 (3), 145–197.Google Scholar
Brady, J. F. & Durlofsky, L. J. 1988 The sedimentation rate of disordered suspensions. Phys. Fluids 31 (4), 717–727.Google Scholar
Brinkman, H. C. 1947 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27–34.Google Scholar
Carman, P. C. 1937 Fluid flow through granular beds. Trans. Inst. Chem. Engrs 15, 150–166.Google Scholar
ten Cate, A., Nieuwstad, C. H., Derksen, J. J. & van den Akker, H. E. A. 2002 Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 14 (11), 4012–4025.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.CrossRefGoogle Scholar
Darcy, H. P. G. 1856 Les fontanes publiques de la ville de Dijon. Dalmont.Google Scholar
Davis, R. H. & Acrivos, A. 1985 Sedimentation of noncolloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mech. 17, 91–118.Google Scholar
Derksen, J. J. & Sundaresan, S. 2007 Direct numerical simulations of dense suspensions: wave instabilities in liquid–fluidized beds. J. Fluid Mech. 587, 303–336.Google Scholar
Derksen, J. J. & van den Akker, H. E. A. 1999 Large-eddy simulations on the flow driven by a Rushton turbine. AIChE J. 45, 209–221.Google Scholar
Eggels, J. G. M. & Somers, J. A. 1995 Numerical simulation of free convective flow using the lattice-Boltzmann scheme. Intl J. Heat Fluid Flow 16 (5), 357–364.Google Scholar
Ergun, S. 1952 Fluid flow through packed columns. Chem. Engng Prog. 48 (2), 89–94.Google Scholar
Garside, J. & Al-Dibouni, M. R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid–liquid systems. Ind. Engng Chem. Process Des. Dev. 16, 206–214.Google Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic.Google Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.Google Scholar
Higuera, F. J. & Jimenez, J. 1989 Boltzmann approach to lattice gas simulations. Europhys. Lett. 9 (7), 663–668.Google Scholar
Higuera, F. J. & Succi, S. 1989 Simulating the flow around a circular cylinder with a lattice Boltzmann equation. Europhys. Lett. 8 (6), 517–521.Google Scholar
Higuera, F. J., Succi, S. & Benzi, R. 1989 Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9 (4), 345–349.Google Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001 The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 213–241.Google Scholar
van der Hoef, M. A., Beetstra, R. & Kuipers, J. A. M. 2005 Lattice-Boltzmann simulations of low-Reynolds-number flow past mono- and bidisperse arrays of spheres: results for the permeability and drag force. J. Fluid Mech. 528, 233–254.Google Scholar
Igci, Y. & Sundaresan, S. 2011 Constitutive models for filtered two-fluid models of fluidized gas–particle flows. Ind. Engng Chem. Res. 50, 13190–13201.Google Scholar
Kim, S. & Karilla, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Kim, S. & Russel, W. B. 1985 Modelling of porous media by renormalization of the Stokes equations. J. Fluid Mech. 154, 269–286.Google Scholar
Koch, D. L. & Sangani, A. S. 1999 Particle pressure and marginal stability limits for a homogeneous monodisperse gas–fluidized bed: kinetic theory and numerical simulations. J. Fluid Mech. 400, 229–263.Google Scholar
Kozeny, J. 1927 Ueber kapillare Leitung des Wassers in Boden. Sitz. ber. Akad. Wiss. Wien 136 (2a), 271–306.Google Scholar
Kriebitzsch, S. H. L., van Der Hoef, M. A. & Kuipers, J. A. M. 2013 Fully resolved simulation of a gas-fluidized bed: a critical test of DEM models. Chem. Engng Sci. 91, 1–4.CrossRefGoogle Scholar
Ladd, A. J. C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.Google Scholar
Ladd, A. J. C. 1997 Sedimentation of homogeneous suspensions of non-Brownian spheres. Phys. Fluids 9 (3), 491–499.Google Scholar
Li, J. & Kuipers, J. A. M. 2003 Gas–particle interactions in dense gas–fluidized beds. Chem. Engng Sci. 58, 711–718.Google Scholar
McNamara, G. R. & Zanetti, G. 1988 Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61 (20), 2332–2335.Google Scholar
Nguyen, N.-Q. & Ladd, A. J. C. 2002 Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 66, 046708.Google Scholar
Nguyen, N.-Q. & Ladd, A. J. C. 2005 Sedimentation of hard-sphere suspensions at low Reynolds number. J. Fluid Mech. 525, 73–104.Google Scholar
Ozel, A., Fede, P. & Simonin, O. 2013 Development of filtered Euler–Euler two-phase model for circulating fluidised bed: high resolution simulation, formulation and a priori analyses. Intl J. Multiphase Flow 55, 43–63.Google Scholar
Pepiot, P. & Desjardins, O. 2012 Numerical analysis of the dynamics of two- and three-dimensional fluidized bed reactors using an Euler–Lagrange approach. Powder Technol. 220, 104–121.CrossRefGoogle Scholar
Qian, Y. H., d’Humieres, D. & Lallemand, P. 1992 Lattice BGK for the Navier–Stokes equations. Europhys. Lett. 17, 479–484.Google Scholar
Radl, S. & Sundaresan, S. 2014 A drag model for filtered Euler–Lagrange simulations of clustered gas–particle suspensions. Chem. Engng Sci. 117, 416–425.Google Scholar
Richardson, J. F. & Zaki, W. N. 1954 Sedimentation and fluidisation. Part 1. Trans. Inst. Chem. Engrs 32, 35–53.Google Scholar
Somers, J. A. 1993 Direct simulation of fluid flow with cellular automata and the lattice-Boltzmann equation. Appl. Sci. Res. 51 (1–2), 127–133.Google Scholar
Sundaresan, S. 2000 Modeling the hydrodynamics of multiphase flow reactors: current status and challenges. AIChE J. 46 (6), 1102–1105.Google Scholar
Tenneti, S., Garg, R. & Subramaniam, S. 2011 Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Intl J. Multiphase Flow 37, 1072–1092.Google Scholar
Wen, C. Y. & Yu, Y. H. 1966 Mechanics of fluidization. Chem. Engng Prog. 62, 100–111.Google Scholar
Wylie, J. J., Koch, D. L. & Ladd, A. J. C. 2003 Rheology of suspensions with high particle inertia and moderate fluid inertia. J. Fluid Mech. 480, 95–118.Google Scholar
Zhou, Q. & Fan, L. S. 2014 A second-order accurate immersed boundary-lattice Boltzmann method for particle-laden flows. J. Comput. Phys. 268, 269–301.Google Scholar