We examine the natural ventilation flows which develop when a low-level heat source interacts with a distributed zone of cooling at high level in an enclosed space. We develop some new analogue laboratory experiments in which we use a saline plume to model a localized heat source and a heated plate to model a distributed source of cooling. The experiments show that in a building with a low-level point source of heating, a two-layer steady stratification develops in which the depth of the lower layer decreases as the intensity of the cooling at the ceiling increases. We develop a theoretical model which accounts for the penetrative entrainment across the interface associated with the convection in the upper layer. We show that this becomes more dominant as the cooling increases and eventually the room becomes well-mixed. We discuss the role of such distributed cooling on the design of natural ventilation and its ability to provide sufficient flow and adequate temperature control.

A vertical cylindrical tube is partially immersed in a water-filled container and pressurized to lower the fluid level inside the tube. A sudden release of the pressure in the tube creates a singularity on top of the rising free surface. At the very beginning of the process a jet emerges at the centre of the surface, the strength of which strongly depends on the initial shape of the meniscus. Here, the time-evolution of the complex shape of the free surface and the flow around the cylindrical tube are analysed using high-speed imaging, particle image velocimetry, and numerical simulations. The tubular jet is found to be created by the following series of events, which eventually lead to the flow focusing at the tube's centre. A circular surface wave, produced by the funnelling of flow into the tube, is pushed inwards by the radial flow directly underneath the surface. As the wave moves inward and eventually collapses at the centre of the tube, a bump of fluid grows in the centre due to the converging flow in the bulk. This converging flow continues to feed the jet after the circular wave has collapsed. The singularity of the wave collapse is manifested in the initial sharp tip of the jet. All of the above events are traced back to a single origin: the convergence of the flow as it enters the tube. Movies are available with the online version of the paper.

This paper studies the unsteady behaviour and linear stability of the flow in a collapsible channel using a fluid–beam model. The solid mechanics is analysed in a plane strain configuration, in which the principal stretch is defined with a zero initial strain. Two approaches are employed: unsteady numerical simulations solving the nonlinear fully coupled fluid–structure interaction problem; and the corresponding linearized eigenvalue approach solving the Orr–Sommerfeld equations modified by the beam. The two approaches give good agreement with each other in predicting the frequencies and growth rates of the perturbation modes, close to the neutral curves. For a given Reynolds number in the range of 200–600, a cascade of instabilities is discovered as the wall stiffness (or effective tension) is reduced. Under small perturbation to steady solutions for the same Reynolds number, the system loses stability by passing through a succession of unstable zones, with mode number increasing as the wall stiffness is decreased. It is found that this cascade structure can, in principle, be extended to many modes, depending on the parameters. A puzzling ‘tongue’ shaped stable zone in the wall stiffness–Re space turns out to be the zone sandwiched by the mode-2 and mode-3 instabilities. Self-excited oscillations dominated by modes 2–4 are found near their corresponding neutral curves. These modes can also interact and form period-doubling oscillations. Extensive comparisons of the results with existing analytical models are made, and a physical explanation for the cascade structure is proposed.

This paper considers the dynamics of a rigid body interacting with point vortices in a perfect fluid. The fluid velocity is obtained using the classical complex variables theory and conformal transformations. The equations of motion of the solid–fluid system are formulated in terms of the solid variables and the position of the point vortices only. These equations are applied to study the dynamic interaction of an elliptic cylinder with vortex pairs because of its relevance to understanding the swimming of fish in an ambient vorticity field. Two families of relative equilibria are found: moving Föppl equilibria; and equilibria along the ellipse's axis of symmetry (the axis perpendicular to the direction of motion). The two families of relative equilibria are similar to those present in the classical problem of flow past a fixed body, but their stability differs significantly from the classical ones.

The study presents a force theory for incompressible flow about several solid bodies, which enables us to examine the force contribution to each body from individual fluid elements. By employing auxiliary potential functions, we decompose hydrodynamic forces in terms of the unsteadiness of the incoming stream, vorticity within the flow, and surface vorticity on the solid bodies. The usefulness of this force decomposition is illustrated by examining separated flow about several circular cylinders. Guidelines were obtained for finding an optimal arrangement to achieve significantly small drag exerted on the cylinders.

Simple analytical relations for the bow wave generated by a ship in steady motion are given. Specifically, simple expressions that define the height of a ship bow wave, the distance between the ship stem and the crest of the bow wave, the rise of water at the stem, and the bow wave profile, explicitly and without calculations, in terms of the ship speed, draught, and waterline entrance angle, are given. Another result is a simple criterion that predicts, also directly and without calculations, when a ship in steady motion cannot generate a steady bow wave. This unsteady-flow criterion predicts that a ship with a sufficiently fine waterline, specifically with waterline entrance angle 2αE smaller than approximately 25°, may generate a steady bow wave at any speed. However, a ship with a fuller waterline (25°<2αE) can only generate a steady bow wave if the ship speed is higher than a critical speed, defined in terms of αE by a simple relation. No alternative criterion for predicting when a ship in steady motion does not generate a steady bow wave appears to exist. A simple expression for the height of an unsteady ship bow wave is also given. In spite of their remarkable simplicity, the relations for ship bow waves obtained in the study (using only rudimentary physical and mathematical considerations) are consistent with experimental measurements for a number of hull forms having non-bulbous wedge-shaped bows with small flare angle, and with the authors' measurements and observations for a rectangular flat plate towed at a yaw angle.

Motivated by the study of blood flow in a curved artery, we consider fluid flow through a curved pipe of uniform curvature, δ, driven by a prescribed oscillatory axial pressure gradient. The curved pipe has finite (as opposed to asymptotically small) curvature, and we determine the effects of both the centrifugal and Coriolis forces on the flow. In addition to δ, the flow is parameterized by the Dean number, D, the Womersley number, α, and a secondary streaming Reynolds number, Rs. Asymptotic solutions are developed for the case when δ≪1, α≪1 and the magnitude of the axial pressure gradient is small, using regular perturbation techniques. For intermediate values of the governing parameters, a pseudospectral code is used to obtain numerical solutions. For flows driven by a sinusoidal pressure gradient (D=0), we identify three distinct classes of stable solutions: 2π-periodic symmetric, 2π-periodic asymmetric, and asymmetric solutions that are either quasi-periodic, or periodic with period 2πk for k∈ 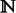. The transition between solutions is dependent on the value of δ; thus pipes with finite curvature may exhibit qualitatively different transitions between the solution classes as the governing parameters are varied from those of curved pipes with asymptotically small curvature. When α≫1, matched asymptotic expansions are used to simplify the system, and the resulting equations are solved analytically for Rs≪1, δ≪1 and numerically for larger parameter values. We then determine the effect of a non-zero steady component of the pressure gradient (D≠0), and show that, for certain parameter values, when D is above a critical value the periodic asymmetric solutions regain spatial symmetry. Finally, we show that the effects of finite curvature can lead to substantial quantitative differences in the wall shear stress distribution and discuss briefly the physiological implications of the results for blood flow in arteries.

It is shown that the Euler hydrodynamics for vortical flows of an ideal fluid is equivalent to the equations of motion of a charged compressible fluid moving due to a self-consistent electromagnetic field. The velocity of new auxiliary fluid coincides with the velocity component normal to the vorticity line for the primitive equations. Therefore this new hydrodynamics represents hydrodynamics of vortex lines. Their compressibility reveals a new mechanism for three-dimensional incompressible vortical flows connected with breaking (or overturning) of vortex lines which can be considered as one of the variants of collapses. Transition to the Lagrangian description in the new hydrodynamics corresponds, for the original Euler equations, to a mixed Lagrangian–Eulerian description – the vortex line representation (VLR). The Jacobian of this mapping defines the density of vortex lines. It is shown also that application of VLR to the Navier–Stokes equations results in an equation of diffusive type for the Cauchy invariant. The diffusion tensor for this equation is defined by the VLR metric.

We model the behaviour of isolated sources of finite radius and volume flux which experience a sudden drop in buoyancy flux, generalizing the previous theory presented in Scase et al. (J. Fluid Mech., vol. 563, 2006, p. 443). In particular, we consider the problem of the source of an established plume suddenly increasing in area to provide a much wider plume source. Our calculations predict that, while our model remains applicable, the plume never fully pinches off into individual rising thermals.

We report the results of a large number of experiments, which provide an ensemble to compare to theoretical predictions. We find that provided the source conditions are weakened in such a way that the well-known entrainment assumption remains valid, the established plume is not observed to pinch off into individual thermals. Further, not only is pinch-off not observed in the ensemble of experiments, it cannot be observed in any of the individual experiments. We consider both the temporal evolution of the plume profile and a concentration of passive tracer, and show that our model predictions compare well with our experimental observations.

It is known that, in a linear shear flow, fluid inertia causes a particle to spin more slowly than the surrounding fluid. The present experiments performed with a sphere with fixed centre, but free to rotate in a fluid undergoing solid-body rotation around a horizontal axis indicate that the spin rate of the sphere can be larger than that of the flow when the sphere is sufficiently far from the axis. Numerical simulations at Reynolds number 5≤Re≤200 confirm this observation. To gain a better understanding of the phenomenon, the rotating flow is decomposed into two shear flows along orthogonal directions. It is found numerically that the cross-stream shear has a much stronger effect on the particle spin rate than the streamwise shear. The region of low stress at the back of the sphere is affected by the shear component of the incident flow. While for the streamwise case the shift is minor, it is significant for cross-stream shear. The results are interpreted on the basis of the effect of the shear flow components on the quasi-toroidal vortex attached in the sphere's near wake. The contributions of streamwise and cross-stream shear to the particle spin can be linearly superposed for Re=20 and 50.

Turbulence and mixing are generated by the shear between two counter-flowing layers in hydraulically controlled buoyancy-driven exchange flows through a constriction. From direct measurements of the density distribution and the amount of turbulent mixing in steady laboratory exchange flows we determine the overall efficiency of the mixing. For sufficiently large Reynolds numbers the mixing efficiency is 0.11(±0.01), independent of the aspect ratio and other details of constriction geometry, in good agreement with a scaling analysis. We conclude that the mixing in shear flows of this type has an overall efficiency significantly less than the maximum value widely proposed for stratified turbulence.

This paper presents the first detailed comparisons between experiments and direct numerical simulations (DNS) of inertial particle clustering in nearly isotropic ‘box turbulence’. The experimental system consists of a box 38cm in each dimension with fans in the eight corners that sustain nearly isotropic turbulence in the centre of the box. We inject hollow glass spheres with a mean diameter of 6 μm and measure the locations of several hundred particles in a 1 cm3 volume in the centre of the box using three-dimensional digital holographic particle imaging. We observe particle concentration fluctuations that result from inertial clustering (sometimes called ‘preferential concentration’). The radial distribution function (RDF), a statistical measure of clustering, has been calculated from the particle position field. We select this measure because of its relevance to the collision kernel for particles. DNS of the equivalent system, with nearly perfect parameter overlap, have also been performed. We observe good agreement between the RDF predictions of the DNS and the experimental observations, despite some challenges in the interpretation of the experiments. The results provide important guidance on ways to improve the measurement.

It is now well-established that the liquid adjacent to a solid need not be stationary – it can slip. How this slip occurs is unclear. We present molecular-dynamics (MD) simulation data and results from an analytical model which support two mechanisms of slip. At low levels of forcing, the potential field generated by the solid creates a ground state which the liquid atoms preferentially occupy. Liquid atoms hop through this energy landscape from one equilibrium site to another according to Arrhenius dynamics. Visual evidence of the trajectories of individual atoms on the solid surface supports the view of localized hopping, independent of the dynamics outside a local neighbourhood. We call this defect slip. At higher levels of forcing, the entire layer slips together, obviating the need for localized defects and resulting in the instantaneous motion of all atoms adjacent to the solid. The appearance of global slip leads to an increase in the number of slipping atoms and consequently an increase in the slip length. Both types of slip observed in the MD simulations are described by a dynamical model in which each liquid atom experiences a force from its neighbouring liquid atoms and the solid atoms of the boundary, is sheared by the overlying liquid, and damped by the solid. In agreement with the MD observations, this model predicts that above a critical value of forcing, localized slipping occurs in which atoms are driven from low-energy sites, but only if there is a downstream site which has been vacated. Also as observed, above a second critical value, all the liquid atoms adjacent to the wall slip. Finally, the dynamical equation predicts that at extremely large values of forcing, the slip length approaches a constant value, in agreement with the MD simulation results.

This paper is concerned with steady and unsteady flow rate limitations in open capillary channels under low-gravity conditions. Capillary channels are widely used in Space technology for liquid transportation and positioning, e.g. in fuel tanks and life support systems. The channel observed in this work consists of two parallel plates bounded by free liquid surfaces along the open sides. The capillary forces of the free surfaces prevent leaking of the liquid and gas ingestion into the flow.

In the case of steady stable flow the capillary pressure balances the differential pressure between the liquid and the surrounding constant-pressure gas phase. Increasing the flow rate in small steps causes a decrease of the liquid pressure. A maximum steady flow rate is achieved when the flow rate exceeds a certain limit leading to a collapse of the free surfaces due to the choking effect. In the case of unsteady flow additional dynamic effects take place due to flow rate transition and liquid acceleration. The maximum flow rate is smaller than in the case of steady flow. On the other hand, the choking effect does not necessarily cause surface collapse and stable temporarily choked flow is possible under certain circumstances.

To determine the limiting volumetric flow rate and stable flow dynamic properties, a new stability theory for both steady and unsteady flow is introduced. Subcritical and supercritical (choked) flow regimes are defined. Stability criteria are formulated for each flow type. The steady (subcritical) criterion corresponds to the speed index defined by the limiting longitudinal small-amplitude wave speed, similar to the Mach number. The unsteady (supercritical) criterion for choked flow is defined by a new characteristic number, the dynamic index. It is based on pressure balances and reaches unity at the stability limit.

The unsteady model based on the Bernoulli equation and the mass balance equation is solved numerically for perfectly wetting incompressible liquids. The unsteady model and the stability theory are verified by comparison to results of a sounding rocket experiment (TEXUS 41) on capillary channel flows launched in December 2005 from ESRANGE in north Sweden. For a clear overview of subcritical, supercritical, and unstable flow, parametric studies and stability diagrams are shown and compared to experimental observations.

This paper is concerned with utilizing the acoustic analogy approach to predict the sound from unheated supersonic jets. Previous attempts have been unsuccessful at making such predictions over the Mach number range of practical interest. The present paper, therefore, focuses on implementing the refinements needed to accomplish this objective. The important effects influencing peak supersonic noise are found to be source convection, mean flow refraction, mean flow amplification, and source non-compactness. It appears that the last two effects have not been adequately dealt with in the literature. For the first of these this is because the usual parallel flow models produce most of the amplification in the so-called critical layer where the solution becomes singular and, therefore, causes the predicted sound field to become infinite. We deal with this by introducing a new weakly non-parallel flow analysis that eliminates the critical layer singularity. This has a strong effect on the shape of the peak noise spectrum. The last effect places severe demands on the source models at the higher Mach numbers because the retarded-time variations significantly increase the sensitivity of the radiated sound to the source structure in this case. A highly refined (non-separable) source model is, therefore, introduced in this paper.

Laser-induced fluorescence was used to measure the lateral dispersion of passive solute in random arrays of rigid, emergent cylinders of solid volume fraction φ=0.010–0.35. Such densities correspond to those observed in aquatic plant canopies and complement those in packed beds of spheres, where φ≥0.5. This paper focuses on pore Reynolds numbers greater than Res=250, for which our laboratory experiments demonstrate that the spatially averaged turbulence intensity and Kyy/(Upd), the lateral dispersion coefficient normalized by the mean velocity in the fluid volume, Up, and the cylinder diameter, d, are independent of Res. First, Kyy/(Upd) increases rapidly with φ from φ =0 to φ=0.031. Then, Kyy/(Upd) decreases from φ=0.031 to φ=0.20. Finally, Kyy/(Upd) increases again, more gradually, from φ=0.20 to φ=0.35. These observations are accurately described by the linear superposition of the proposed model of turbulent diffusion and existing models of dispersion due to the spatially heterogeneous velocity field that arises from the presence of the cylinders. The contribution from turbulent diffusion scales with the mean turbulence intensity, the characteristic length scale of turbulent mixing and the effective porosity. From a balance between the production of turbulent kinetic energy by the cylinder wakes and its viscous dissipation, the mean turbulence intensity for a given cylinder diameter and cylinder density is predicted to be a function of the form drag coefficient and the integral length scale lt. We propose and experimentally verify that lt=min{d, 〈sn〉A}, where 〈sn〉A is the average surface-to-surface distance between a cylinder in the array and its nearest neighbour. We farther propose that only turbulent eddies with mixing length scale greater than d contribute significantly to net lateral dispersion, and that neighbouring cylinder centres must be farther than r* from each other for the pore space between them to contain such eddies. If the integral length scale and the length scale for mixing are equal, then r*=2d. Our laboratory data agree well with predictions based on this definition of r*.

Lesshafft & Huerre (Phys. Fluids, 2007; vol. 19, 024102) have recently studied the transition from convective to absolute instability in hot round jets, for which absolute instability is led by axisymmetric perturbations and enhanced when lowering the jet density. The present paper analyses similarly the counterpart problem of wake flows, and establishes that absolute instability is then led by a large-scale helical wake mode favoured when the wake is denser than the surrounding fluid. This generalizes to variable density and compressible wakes the results of Monkewitz (J. Fluid Mech. vol 192, 1988, p. 561). Furthermore, we show that in a particular range of density ratios, the large-scale helical wake mode can become absolutely unstable by increasing only the Mach number up to high subsonic values. This possibility of an absolute instability triggered by an increase of the Mach number is opposite to the behaviour previously described in shear flows such as plane mixing layers and axisymmetric jets. A physical interpretation based on the action of the baroclinic torque is proposed. An axisymmetric short-scale mode, similar to that observed in plane mixing layers, leads the transition in light wakes, but the corresponding configurations require large counterflow for the instability to be absolute.

These results suggest that the low-frequency oscillation present in afterbody wakes may be due to a nonlinear global mode triggered by a local absolute instability, since the azimuthal wavenumber and absolute frequency of the helical wake mode agree qualitatively with observations.

The turbulent flow in a two-dimensional channel with roughness on one wall is investigated using experiments and direct numerical simulations (DNS). The elements have a square cross-section with height k=0.1H (H is the channel half-width) and a streamwise spacing of 4k. The Reynolds number Reτr, based on the friction velocity at the rough wall and H, is in the range 300–1100. Particular attention is given to the rough-wall side. Measured turbulence intensities, length scales, leading terms in the turbulent kinetic energy budget, and velocity spectra are compared with those obtained from the DNS. Close agreement is found, yielding support for the simplifying assumptions in the experiment (notably local isotropy and Taylor's hypothesis) and the adequacy of the spatial resolution in the simulation. Overall, the profiles of the Reynolds normal stresses on the roughness side are almost independent of Reτr, when normalized by outer variables. Energy spectra at different locations above the rough wall collapse well at high wavenumbers, when normalized by Kolmogorov scales. In contrast to previous studies, a region of negative energy production near the location of the maximum streamwise velocity is not observed. Comparison with a smooth-wall channel, at similar values of the friction-velocity Reynolds number, highlights differences only in the streamwise velocity component near the wall.

A horizontal fluid layer heated from below and rotating about a vertical axis in the presence of a vertical magnetic field is considered. From earlier work it is known that the onset of convection in a rotating layer usually occurs in the form of travelling waves attached to the vertical sidewalls of the layer. It is found that this behaviour persists when a vertical magnetic field is applied. When the Elsasser number Λ is kept constant and the sidewall is thermally insulating the critical Rayleigh number Rc increases in proportion to the rotation rate described by the square root of the Taylor number, τ. This asymptotic relationship is found for an electrically highly conducting sidewall as well as for an electrically insulating one. At fixed rotation rate for Q≫τ, Rc grows in proportion to Q when the sidewall is electrically highly conducting, and in proportion to Q3/4 when the sidewall is electrically insulating. Here Q is the Chandrasekhar number which is a measure of the magnetic energy density, and a thermally insulating sidewall has been assumed. Of particular interest is the possibility that the magnetic field counteracts the stabilizing influence of rotation on the onset of sidewall convection in the case of thermally insulating sidewalls. When the sidewall is thermally highly conducting, Rc for the sidewall mode grows in proportion to τ4/3. This asymptotic behaviour is found for both cases of electrical boundary conditions, but it no longer precedes the onset of bulk convection for Λ ≳ 1.