Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T06:58:46.888Z Has data issue: false hasContentIssue false
  • English
  • Français

The virtual power principle in fluid mechanics

Published online by Cambridge University Press:  11 March 2014

Yongliang Yu
Yongliang Yu*
Affiliation:
School of Physics, University of the Chinese Academy of Sciences, Beijing 100049, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A conceptual framework on analytical mechanics for continuous fluid medium, which connects the fluid motion and all of the (internal and external) forces with mechanical power, is proposed by using the virtual power and the virtual velocity. Based on this framework, it is found that the internal virtual power is equal to the external virtual power in fluid dynamics, which is called the virtual power principle. This framework is also proved to be equivalent to the vector dynamics (Cauchy’s equation or Navier–Stokes equation). Furthermore, based on the virtual power principle, a theorem is introduced for continuous fluid medium, which indicates the relationship between the force (or torque) acting on a body immersed in a fluid and the specified virtual power. Subsequently, according to Galilean invariance, the detailed relationship for Newtonian fluids in incompressible flows is derived and used to illustrate the mechanisms on instantaneous forces: the added inertial effects, the boundary energy flux and dissipation effects, the vortex contribution, and the explicit body force contribution. As an application of the principle, the advantage of the V formation flight of geese is preliminarily discussed in the view of aerodynamics. Specifically, the total drag of the flock is reduced by contrast with the simple sum of the drag in solo fight and the optimal angle of V ranges from 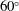$60^{\circ }$ to 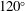$120^{\circ }$. The principle could be a useful approach to reveal the contributions of the flow structures and the moving or deforming boundaries to the force and torque acting on a body, especially in a multibody system.

JFM classification

Aerodynamics: Aerodynamics Mathematical Foundations: General fluid mechanics Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 310 - 328
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chang, C. C. 1992 Potential flow and forces for incompressible viscous flow. Proc. R. Soc. Lond. A 437, 517–525.Google Scholar
Chang, C. C. & Lei, S. Y. 1996 On the sources of aerodynamic forces: steady flow around a cylinder or a sphere. Proc. R. Soc. Lond. A 452, 2369–2395.Google Scholar
Chang, C. C., Yang, S. H. & Chu, C. C. 2008 A many-body force decomposition with applications to flow about bluff bodies. J. Fluid Mech. 600, 95–104.CrossRefGoogle Scholar
Hamman, C. W., Klewicki, J. C. & Kirby, R. M. 2008 On the Lamb vector divergence in Navier–Stokes flows. J. Fluid Mech. 619, 261–284.CrossRefGoogle Scholar
Hedrick, T. L., Tobalske, B. W. & Biewener, A. A. 2002 Estimates of circulation and gait change based on a three-dimensional kinematic analysis of flight in cockatiels (Nymphicus hollandicus) and ringed turtle–doves (Streptopelia risoria). J. Expl Biol. 205, 1389–1409.CrossRefGoogle ScholarPubMed
Howe, M. 1989 On unsteady surface forces, and sound produced by the normal chopping of a rectilinear vortex. J. Fluid Mech. 206, 131–153.CrossRefGoogle Scholar
Howe, M. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. J. Mech. Appl. Maths 48, 401–426.CrossRefGoogle Scholar
Howe, M., Lauchle, G. C. & Wang, J. 2001 Aerodynamic lift and drag fluctuations of a sphere. J. Fluid Mech. 436, 41–57.CrossRefGoogle Scholar
Hsieh, C. T., Kung, C. F., Chang, C. C. & Chu, C. C. 2010 Unsteady aerodynamics of dragonfly using a simple wing–wing model from the perspective of a force decomposition. J. Fluid Mech. 663, 233–252.CrossRefGoogle Scholar
Hummel, D. 1995 Formation flight as an energy-saving mechanism. Isr. J. Zool. 41, 261–278.Google Scholar
Lebar Bajec, I. & Heppner, F. H. 2009 Organized flight in birds. Anim. Behav. 78, 777–789.CrossRefGoogle Scholar
Lee, J. J., Hsieh, C. T., Chang, C. C. & Chu, C. C. 2012 Vorticity forces on an impulsively started finite plate. J. Fluid Mech. 694, 464–492.CrossRefGoogle Scholar
Lissaman, P. & Shollenberger, C. A. 1970 Formation flight of birds. Science 168, 1003–1005.CrossRefGoogle ScholarPubMed
Magnaudet, J. 2011 A ‘reciprocal’ theorem for the prediction of loads on a body moving in an inhomogeneous flow at arbitrary Reynolds number. J. Fluid Mech. 689, 564–604.CrossRefGoogle Scholar
Maugin, G. A. 1980 The method of virtual power in continuum mechanics: application to coupled fields. Acta Mechanica 35, 1–70.CrossRefGoogle Scholar
Pao, Y. H., Wang, L. S. & Chen, K. C. 2011 Principle of virtual power for thermomechanics of fluids and solids with dissipation. Intl J. Engng Sci. 49, 1502–1516.CrossRefGoogle Scholar
Quartapelle, L. & Napolitano, M. 1983 Force and moment in incompressible flows. AIAA J. 21, 911–913.CrossRefGoogle Scholar
Ragazzo, C. G. & Tabak, E. 2007 On the force and torque on systems of rigid bodies: a remark on an integral formula due to howe. Phys. Fluids 19, 057108.CrossRefGoogle Scholar
Rayner, J. M. 2001 Fat and formation in flight. Nature 413, 685–686.CrossRefGoogle ScholarPubMed
Spedding, G. 1987a The wake of a kestrel (Falco tinnunculus) in gliding flight. J. Expl Biol. 127, 45–57.CrossRefGoogle Scholar
Spedding, G. 1987a The wake of a kestrel (Falco tinnunculus) in flapping flight. J. Expl Biol. 127, 59–78.CrossRefGoogle Scholar
Weimerskirch, H., Martin, J., Clerquin, Y., Alexandre, P. & Jiraskova, S. 2001 Energy saving in flight formation. Nature 413, 697–698.CrossRefGoogle ScholarPubMed
Wells, J. C. 1996 A geometrical interpretation of force on a translating body in rotational flow. Phys. Fluids 8, 442–450.CrossRefGoogle Scholar
Wu, J. Z., Ma, H. Y. & Zhou, M. D. 2006 Vorticity and vortex dynamics. Springer-Verlag.CrossRefGoogle Scholar