Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:44:10.448Z Has data issue: false hasContentIssue false
  • English
  • Français

Vertical natural convection: application of the unifying theory of thermal convection

Published online by Cambridge University Press:  06 January 2015

Chong Shen Ng Open the ORCID record for Chong Shen Ng [Opens in a new window] ,
Andrew Ooi ,
Detlef Lohse  and
Daniel Chung
Chong Shen Ng*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Andrew Ooi
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Detlef Lohse
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J. M. Burgers Center for Fluid Dynamics and MESA+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
Daniel Chung
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Results from direct numerical simulations of vertical natural convection at Rayleigh numbers 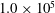$1.0\times 10^{5}$–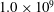$1.0\times 10^{9}$ and Prandtl number 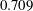$0.709$ support a generalised applicability of the Grossmann–Lohse (GL) theory, which was originally developed for horizontal natural (Rayleigh–Bénard) convection. In accordance with the GL theory, it is shown that the boundary-layer thicknesses of the velocity and temperature fields in vertical natural convection obey laminar-like Prandtl–Blasius–Pohlhausen scaling. Specifically, the normalised mean boundary-layer thicknesses scale with the 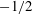$-1/2$-power of a wind-based Reynolds number, where the ‘wind’ of the GL theory is interpreted as the maximum mean velocity. Away from the walls, the dissipation of the turbulent fluctuations, which can be interpreted as the ‘bulk’ or ‘background’ dissipation of the GL theory, is found to obey the Kolmogorov–Obukhov–Corrsin scaling for fully developed turbulence. In contrast to Rayleigh–Bénard convection, the direction of gravity in vertical natural convection is parallel to the mean flow. The orientation of this flow presents an added challenge because there no longer exists an exact relation that links the normalised global dissipations to the Nusselt, Rayleigh and Prandtl numbers. Nevertheless, we show that the unclosed term, namely the global-averaged buoyancy flux that produces the kinetic energy, also exhibits both laminar and turbulent scaling behaviours, consistent with the GL theory. The present results suggest that, similar to Rayleigh–Bénard convection, a pure power-law relationship between the Nusselt, Rayleigh and Prandtl numbers is not the best description for vertical natural convection and existing empirical relationships should be recalibrated to better reflect the underlying physics.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 764 , 10 February 2015 , pp. 349 - 361
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Batchelor, G. K. 1954 Heat transfer by free convection across a closed cavity between vertical boundaries at different temperatures. Q. Appl. Maths 12, 209–233.CrossRefGoogle Scholar
Calzavarini, E., Doering, C. R., Gibbon, J. D., Lohse, D., Tanabe, A. & Toschi, F. 2006 Exponentially growing solutions in homogeneous Rayleigh–Bénard convection. Phys. Rev. E 73 (3), 035301.CrossRefGoogle ScholarPubMed
Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard turbulence. Phys. Fluids 17, 055107.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chait, A. & Korpela, S. A. 1989 The secondary flow and its stability for natural convection in a tall vertical enclosure. J. Fluid Mech. 200, 189–216.CrossRefGoogle Scholar
Chavanne, X., Chillà, F., Castaing, B., Hébral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79 (19), 3648–3651.CrossRefGoogle Scholar
Chavanne, X., Chillà, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13 (5), 1300–1320.CrossRefGoogle Scholar
Churchill, S. W. & Chu, H. H. S. 1975 Correlating equations for laminar and turbulent free convection from a vertical plate. Intl J. Heat Mass Transfer 18, 1323–1329.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Elder, J. W. 1965 Turbulent free convection in a vertical slot. J. Fluid Mech. 23, 99–111.CrossRefGoogle Scholar
Emran, M. S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.CrossRefGoogle Scholar
George, W. K. & Capp, S. P. 1979 A theory for natural convection turbulent boundary layers next to heated vertical surfaces. Intl J. Heat Mass Transfer 22, 813–826.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection at large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66 (1), 016305.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.CrossRefGoogle Scholar
Kaczorowski, M. & Wagner, C. 2009 Analysis of the thermal plumes in turbulent Rayleigh–Bénard convection based on well-resolved numerical simulations. J. Fluid Mech. 618, 89–112.CrossRefGoogle Scholar
Kaczorowski, M. & Xia, K.-Q. 2013 Turbulent flow in the bulk of Rayleigh–Bénard convection: small-scale properties in a cubic cell. J. Fluid Mech. 722, 596–617.CrossRefGoogle Scholar
Kiš, P. & Herwig, H. 2012 The near wall physics and wall functions for turbulent natural convection. Intl J. Heat Mass Transfer 55, 2625–2635.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
Ng, C. S.2013 Direct numerical simulation of natural convection bounded by differentially heated vertical walls. MPhil thesis, University of Melbourne.Google Scholar
Ng, C. S., Chung, D. & Ooi, A. 2013 Turbulent natural convection scaling in a vertical channel. Intl J. Heat Fluid Flow 44, 554–562.CrossRefGoogle Scholar
Pallares, J., Vernet, A., Ferre, J. A. & Grau, F. X. 2010 Turbulent large-scale structures in natural convection vertical channel flow. Intl J. Heat Mass Transfer 53, 4168–4175.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Scheel, J. D. & Schumacher, J. 2014 Local boundary layer scales in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 758, 344–373.CrossRefGoogle Scholar
Schmidt, L. E., Calzavarini, E., Lohse, D., Toschi, F. & Verzicco, R. 2012 Axially homogeneous Rayleigh–Bénard convection in a cylindrical cell. J. Fluid Mech. 691, 52–68.CrossRefGoogle Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010a Boundary layers in rotating weakly turbulent Rayleigh–Bénard convection. Phys. Fluids 22, 085103.CrossRefGoogle Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.CrossRefGoogle Scholar
Stevens, R. J. A. M., Verzicco, R. D. & Lohse, D. 2010b Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Tsuji, T. & Nagano, Y. 1988 Characteristics of a turbulent natural convection boundary layer along a vertical flat plate. Intl J. Heat Mass Transfer 31, 1723–1734.CrossRefGoogle Scholar
Versteegh, T. A. M. & Nieuwstadt, F. T. M. 1999 A direct numerical simulation of natural convection between two infinite vertical differentially heated walls scaling laws and wall functions. Intl J. Heat Mass Transfer 42, 3673–3693.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
White, F. M. 1991 Viscous Fluid Flow, 2nd edn. McGraw-Hill.Google Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed