1. Introduction
Shear-induced self-diffusion describes the random and non-affine particle displacements observed in all flows involving granular materials, be they dry or immersed in a liquid (Eckstein, Bailey & Shapiro Reference Eckstein, Bailey and Shapiro1977; Zik & Stavans Reference Zik and Stavans1991; Sierou & Brady Reference Sierou and Brady2004). This process is key in many situations in nature and industry as it drives grain mixing and can significantly enhance heat transfers or counterbalance segregation across sheared granular layers (Rognon & Einav Reference Rognon and Einav2010; Metzger, Rahli & Yin Reference Metzger, Rahli and Yin2013; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Koslover, Chan & Theriot Reference Koslover, Chan and Theriot2017; Thøgersen & Dabrowski Reference Thøgersen and Dabrowski2017; Weijs & Bartolo Reference Weijs and Bartolo2017; Rognon & Macaulay Reference Rognon and Macaulay2021). Yet its description remains incomplete. Widely investigated for low and moderate solid fractions under volume-imposed conditions (Leighton & Acrivos Reference Leighton and Acrivos1987; Breedveld et al. Reference Breedveld, Van Den Ende, Bosscher, Jongschaap and Mellema2002; Leshansky & Brady Reference Leshansky and Brady2005; Olsson Reference Olsson2010; Vollebregt, Van Der Sman & Boom Reference Vollebregt, Van Der Sman and Boom2010; Hatano Reference Hatano2011; Metzger et al. Reference Metzger, Rahli and Yin2013; Saitoh & Kawasaki Reference Saitoh and Kawasaki2020, Reference Saitoh and Kawasaki2022), shear-induced self-diffusion at the continuum scale is described by an effective diffusion coefficient ![]() $D=f(\phi )\,\dot {\gamma } d^2$ featuring dependencies on the flow shear rate
$D=f(\phi )\,\dot {\gamma } d^2$ featuring dependencies on the flow shear rate ![]() $\dot {\gamma }$ and the particle diameter
$\dot {\gamma }$ and the particle diameter ![]() $d$ (Leighton & Acrivos Reference Leighton and Acrivos1987). However, the nature and origin of
$d$ (Leighton & Acrivos Reference Leighton and Acrivos1987). However, the nature and origin of ![]() $f(\phi )$, a function of the particle solid fraction
$f(\phi )$, a function of the particle solid fraction ![]() $\phi$, remain elusive, especially in the dense regime (Vollebregt et al. Reference Vollebregt, Van Der Sman and Boom2010; Artoni et al. Reference Artoni, Larcher, Jenkins and Richard2021).
$\phi$, remain elusive, especially in the dense regime (Vollebregt et al. Reference Vollebregt, Van Der Sman and Boom2010; Artoni et al. Reference Artoni, Larcher, Jenkins and Richard2021).
During the past two decades, significant progress has been made in understanding the rheological properties of granular systems using the so-called pressure-imposed approach, where instead of imposing the particle volume fraction, one controls the confining particle stress ![]() $P$ (MiDi 2004; Da Cruz et al. Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005). The virtue of this approach is to prescribe the normal stress and let the granular layer dilate or compact accordingly. It conveniently allows measurements close to the jamming transition, i.e. when
$P$ (MiDi 2004; Da Cruz et al. Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005). The virtue of this approach is to prescribe the normal stress and let the granular layer dilate or compact accordingly. It conveniently allows measurements close to the jamming transition, i.e. when ![]() $\phi \to \phi _c$, where
$\phi \to \phi _c$, where ![]() $\phi _c$ is the maximum packing solid fraction. This pressure-imposed approach allowed major progress and in particular the identification of the critical behaviours of the rheological properties of granular flows and dense suspensions (Forterre & Pouliquen Reference Forterre and Pouliquen2008; Boyer, Guazzelli & Pouliquen Reference Boyer, Guazzelli and Pouliquen2011; Guazzelli & Pouliquen Reference Guazzelli and Pouliquen2018). For inertial grains of density
$\phi _c$ is the maximum packing solid fraction. This pressure-imposed approach allowed major progress and in particular the identification of the critical behaviours of the rheological properties of granular flows and dense suspensions (Forterre & Pouliquen Reference Forterre and Pouliquen2008; Boyer, Guazzelli & Pouliquen Reference Boyer, Guazzelli and Pouliquen2011; Guazzelli & Pouliquen Reference Guazzelli and Pouliquen2018). For inertial grains of density ![]() $\rho$, this approach also revealed the scaling relation
$\rho$, this approach also revealed the scaling relation ![]() $D\propto \dot {\gamma } d^2/\sqrt {I}$ between the shear-induced diffusion coefficient
$D\propto \dot {\gamma } d^2/\sqrt {I}$ between the shear-induced diffusion coefficient ![]() $D$ and the inertial number
$D$ and the inertial number ![]() $I=\dot {\gamma }d \sqrt {\rho /P}$, controlling the flow (Kharel & Rognon Reference Kharel and Rognon2017).
$I=\dot {\gamma }d \sqrt {\rho /P}$, controlling the flow (Kharel & Rognon Reference Kharel and Rognon2017).
In this paper, we use pressure-imposed simulations to address the behaviour of the shear-induced self-diffusion coefficient in dense suspensions composed of rigid, non-Brownian and frictional particles immersed in a viscous fluid of viscosity ![]() $\eta$. We first express the shear-induced self-diffusion coefficient
$\eta$. We first express the shear-induced self-diffusion coefficient ![]() $D$ as a function of the viscous number
$D$ as a function of the viscous number ![]() $J = \eta \dot {\gamma }/P$, the analogue of the inertial number for suspensions (Boyer et al. Reference Boyer, Guazzelli and Pouliquen2011; Rognon, Einav & Gay Reference Rognon, Einav and Gay2011; DeGiuli et al. Reference DeGiuli, Düring, Lerner and Wyart2015; Guazzelli & Pouliquen Reference Guazzelli and Pouliquen2018). Then, using the dilatancy laws
$J = \eta \dot {\gamma }/P$, the analogue of the inertial number for suspensions (Boyer et al. Reference Boyer, Guazzelli and Pouliquen2011; Rognon, Einav & Gay Reference Rognon, Einav and Gay2011; DeGiuli et al. Reference DeGiuli, Düring, Lerner and Wyart2015; Guazzelli & Pouliquen Reference Guazzelli and Pouliquen2018). Then, using the dilatancy laws ![]() $\phi (J)$ and
$\phi (J)$ and ![]() $\phi (I)$ of both suspensions and inertial granular media, we find that the shear-induced self-diffusion coefficient
$\phi (I)$ of both suspensions and inertial granular media, we find that the shear-induced self-diffusion coefficient ![]() $D$ of both systems follows a similar scaling relation with the distance to jamming
$D$ of both systems follows a similar scaling relation with the distance to jamming ![]() $\phi _c-\phi$, identifying the function
$\phi _c-\phi$, identifying the function ![]() $f(\phi )=0.027(\phi _c-\phi )^{-1/2}$. This result indicates that particle self-diffusion is oblivious to the origin of the dissipation mechanism (viscous damping forces or elastic granular collisions) and is determined primarily by geometrical effects. Moreover, we show that in suspensions and inertial granular media, the scaling for the particle-shear-induced self-diffusion coefficient stems from a specific random walk process, featuring a constant elementary step length driven at a frequency that increases with the solid fraction.
$f(\phi )=0.027(\phi _c-\phi )^{-1/2}$. This result indicates that particle self-diffusion is oblivious to the origin of the dissipation mechanism (viscous damping forces or elastic granular collisions) and is determined primarily by geometrical effects. Moreover, we show that in suspensions and inertial granular media, the scaling for the particle-shear-induced self-diffusion coefficient stems from a specific random walk process, featuring a constant elementary step length driven at a frequency that increases with the solid fraction.
2. Method
Simulations are performed using a discrete element method initially built for volume-imposed simulations (Mari et al. Reference Mari, Seto, Morris and Denn2014), and then further developed to address pressure-imposed configurations (Athani et al. Reference Athani, Metzger, Forterre and Mari2022). This method solves for the motion of individual, inertialess grains considering frictional, linear elastic contacts and lubrication interactions with neighbouring grains, and an interaction with the imposed external shear flow through a viscous drag. More details about the simulation method can be found in Appendix A.
As shown in figure 1(a), the system is composed of a monolayer of hard bidisperse spheres of mean diameter ![]() $d$ confined between two walls. Black particles constitute the rigid top and bottom walls built out of frozen particles arranged in a disordered configuration. Note that Wang & Brady (Reference Wang and Brady2015) developed a pressure imposed code that, by allowing a finite compressibility of the fluid phase, enables us to use Lees–Edwards boundary conditions, thereby preventing the introduction of solid walls. Here, the bottom wall is fixed, while the top wall, permeable to the fluid, moves horizontally to shear the suspension, but is also free to move vertically. The control parameters are the external pressure
$d$ confined between two walls. Black particles constitute the rigid top and bottom walls built out of frozen particles arranged in a disordered configuration. Note that Wang & Brady (Reference Wang and Brady2015) developed a pressure imposed code that, by allowing a finite compressibility of the fluid phase, enables us to use Lees–Edwards boundary conditions, thereby preventing the introduction of solid walls. Here, the bottom wall is fixed, while the top wall, permeable to the fluid, moves horizontally to shear the suspension, but is also free to move vertically. The control parameters are the external pressure ![]() $P$ acting on the top wall, and the shear rate
$P$ acting on the top wall, and the shear rate ![]() $\dot {\gamma }$ of the imposed background shear flow. In this pressure-imposed configuration, the solid fraction
$\dot {\gamma }$ of the imposed background shear flow. In this pressure-imposed configuration, the solid fraction ![]() $\phi$ is free to adjust owing to the value of the imposed viscous number
$\phi$ is free to adjust owing to the value of the imposed viscous number ![]() $J = \eta \dot {\gamma }/ P$. Importantly, such a configuration was used previously to simulate the transient migration/dilation of a granular layer under changes of boundary conditions (Athani et al. Reference Athani, Metzger, Forterre and Mari2022). The present study is focused on the behaviour of the particle shear-induced self-diffusion coefficient when imposing different viscous numbers
$J = \eta \dot {\gamma }/ P$. Importantly, such a configuration was used previously to simulate the transient migration/dilation of a granular layer under changes of boundary conditions (Athani et al. Reference Athani, Metzger, Forterre and Mari2022). The present study is focused on the behaviour of the particle shear-induced self-diffusion coefficient when imposing different viscous numbers ![]() $J$. We thus report only measurement performed during steady states, for which the particle pressure and volume fraction are homogeneous across the system. Moreover, this pressure-imposed configuration allows us to perform simulations with a fixed degree of overlap between particle as the parameter
$J$. We thus report only measurement performed during steady states, for which the particle pressure and volume fraction are homogeneous across the system. Moreover, this pressure-imposed configuration allows us to perform simulations with a fixed degree of overlap between particle as the parameter ![]() $\tilde {k}=k_n/Pd$, where
$\tilde {k}=k_n/Pd$, where ![]() $k_n$, the particle stiffness, can easily be held constant. Simulations obtained with different values
$k_n$, the particle stiffness, can easily be held constant. Simulations obtained with different values ![]() $\tilde {k} = 10^{3}$,
$\tilde {k} = 10^{3}$, ![]() $10^{4}$ and
$10^{4}$ and ![]() $10^{5}$ show that our results are representative of the rigid grains limit (Da Cruz et al. Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005). We take advantage of the pressure-imposed configuration to explore the system in the ‘dense’ regime, reaching distances to jamming as small as
$10^{5}$ show that our results are representative of the rigid grains limit (Da Cruz et al. Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005). We take advantage of the pressure-imposed configuration to explore the system in the ‘dense’ regime, reaching distances to jamming as small as ![]() $\phi _c-\phi =0.02$, or equivalently,
$\phi _c-\phi =0.02$, or equivalently, ![]() $J=10^{-4}$. The protocol is as follows. We set the external pressure
$J=10^{-4}$. The protocol is as follows. We set the external pressure ![]() $P$ and the shear rate
$P$ and the shear rate ![]() $\dot {\gamma }$, then run the simulation until the suspension reaches a steady state (with homogeneous particle pressure and volume fraction profiles), corresponding to the target viscous number
$\dot {\gamma }$, then run the simulation until the suspension reaches a steady state (with homogeneous particle pressure and volume fraction profiles), corresponding to the target viscous number ![]() $J=\eta \dot {\gamma }/P$. From this point, referred to as
$J=\eta \dot {\gamma }/P$. From this point, referred to as ![]() $t=0$, the simulation is performed for
$t=0$, the simulation is performed for ![]() $30$ additional strain units, over which the particle shear induced self-diffusion coefficient is computed.
$30$ additional strain units, over which the particle shear induced self-diffusion coefficient is computed.

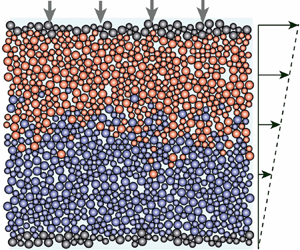
Figure 1. Shear-induced self-diffusion in a two-dimensional suspension and comparison with dry inertial granular media. (a,b) Snapshots of the suspension shown at strains ![]() $\gamma =\dot {\gamma }t=0$ and
$\gamma =\dot {\gamma }t=0$ and ![]() $30$, sheared under high (
$30$, sheared under high (![]() $J=5\times 10^{-2}$) and low (
$J=5\times 10^{-2}$) and low (![]() $J=5\times 10^{-4}$) viscous numbers, respectively. Corresponding movies are available online at https://doi.org/10.1017/jfm.2024.695. (c) Mean square displacements
$J=5\times 10^{-4}$) viscous numbers, respectively. Corresponding movies are available online at https://doi.org/10.1017/jfm.2024.695. (c) Mean square displacements ![]() $\varDelta _y^2/d^2$ versus strain
$\varDelta _y^2/d^2$ versus strain ![]() $\dot {\gamma }t$ obtained for various imposed steady viscous numbers
$\dot {\gamma }t$ obtained for various imposed steady viscous numbers ![]() $J$. Inset: same data plotted versus
$J$. Inset: same data plotted versus ![]() $t/\varPsi$, where
$t/\varPsi$, where ![]() $\varPsi$ is the persistence time. (d) Corresponding particle dimensionless diffusion coefficients
$\varPsi$ is the persistence time. (d) Corresponding particle dimensionless diffusion coefficients ![]() $D/\dot {\gamma }d^2$ versus
$D/\dot {\gamma }d^2$ versus ![]() $J$ (blue diamonds
$J$ (blue diamonds ![]() $\tilde {k}=10^{3}$, blue triangles
$\tilde {k}=10^{3}$, blue triangles ![]() $\tilde {k}=10^{4}$, blue circles
$\tilde {k}=10^{4}$, blue circles ![]() $\tilde {k}=10^{5}$, present study) and comparison with
$\tilde {k}=10^{5}$, present study) and comparison with ![]() $D/\dot {\gamma }d^2$ versus
$D/\dot {\gamma }d^2$ versus ![]() $I$ for a dry inertial granular system (red squares, data from Macaulay & Rognon Reference Macaulay and Rognon2019). The uncertainty on
$I$ for a dry inertial granular system (red squares, data from Macaulay & Rognon Reference Macaulay and Rognon2019). The uncertainty on ![]() $D$ arising from fitting the mean square displacement is
$D$ arising from fitting the mean square displacement is ![]() $\pm 2\,\%$; typical error bars can be appreciated from the dispersion between runs.
$\pm 2\,\%$; typical error bars can be appreciated from the dispersion between runs.
3. Results
In figures 1(a) and 1(b), we illustrate the grain mixing arising from shear-induced diffusion by colour coding the top and bottom particles at ![]() $t=0$. We observe that after 30 strain units, grains have diffused significantly, and that mixing is more pronounced for the lowest viscous number (i.e. for
$t=0$. We observe that after 30 strain units, grains have diffused significantly, and that mixing is more pronounced for the lowest viscous number (i.e. for ![]() $J=5\times 10^{-4}$). To investigate this phenomenology more quantitatively, we measure the particle mean square displacements in the gradient direction
$J=5\times 10^{-4}$). To investigate this phenomenology more quantitatively, we measure the particle mean square displacements in the gradient direction ![]() $\varDelta _y^2(t) = \langle (y_i(t_0+t) - y_i(t_0))^2\rangle$, where
$\varDelta _y^2(t) = \langle (y_i(t_0+t) - y_i(t_0))^2\rangle$, where ![]() $y_i(t)$ is the transverse position of grain
$y_i(t)$ is the transverse position of grain ![]() $i$ at time
$i$ at time ![]() $t$, and the operator
$t$, and the operator ![]() $\langle \cdot \rangle$ denotes a spatial average including all mobile grains and a temporal average including
$\langle \cdot \rangle$ denotes a spatial average including all mobile grains and a temporal average including ![]() $10^3$ reference times
$10^3$ reference times ![]() $t_0$ taken at random during the flow. Figure 1(c) shows the normalized mean square displacements
$t_0$ taken at random during the flow. Figure 1(c) shows the normalized mean square displacements ![]() $\varDelta _y^2/d^2$ versus strain
$\varDelta _y^2/d^2$ versus strain ![]() $\dot {\gamma }t$ obtained for different imposed viscous numbers
$\dot {\gamma }t$ obtained for different imposed viscous numbers ![]() $J\in [10^{-4},10^{-1}]$, or equivalent solid fractions
$J\in [10^{-4},10^{-1}]$, or equivalent solid fractions ![]() $\phi _c-\phi \in [0.02,0.25]$. After a short ballistic regime, where the mean square displacements increase quadratically with strain, the system transitions towards a linear diffusive regime. The corresponding diffusion coefficients are extracted according to the Einstein formula
$\phi _c-\phi \in [0.02,0.25]$. After a short ballistic regime, where the mean square displacements increase quadratically with strain, the system transitions towards a linear diffusive regime. The corresponding diffusion coefficients are extracted according to the Einstein formula ![]() $D = \lim _{ t \to \infty } \varDelta _y^2(t)/2t$, by fitting the mean square displacement, using
$D = \lim _{ t \to \infty } \varDelta _y^2(t)/2t$, by fitting the mean square displacement, using ![]() $\varDelta _y^2/d^2=2 (D/\dot {\gamma }d^2) \dot {\gamma }t$, over the strain range highlighted by the dashed lines (
$\varDelta _y^2/d^2=2 (D/\dot {\gamma }d^2) \dot {\gamma }t$, over the strain range highlighted by the dashed lines (![]() $\gamma \in [8,15]$), where the system has reached its diffusive regime. The resulting shear-induced diffusion coefficients plotted for various values of
$\gamma \in [8,15]$), where the system has reached its diffusive regime. The resulting shear-induced diffusion coefficients plotted for various values of ![]() $J$ in figure 1(d) can be well fitted by the simple power law
$J$ in figure 1(d) can be well fitted by the simple power law ![]() $D(J)/\dot \gamma d^2=0.024 J^{-0.26}$, suggesting that
$D(J)/\dot \gamma d^2=0.024 J^{-0.26}$, suggesting that ![]() $D$ follows the scaling law
$D$ follows the scaling law
For the sake of clarity, all exponents in the following are similarly rounded to the nearest fractional exponent (within error bars). The fitting procedure, best-fit parameters and associated error bars are provided in Appendix B. The latter scaling law indicates that particles in suspensions tend to diffuse more for smaller values of the viscous number ![]() $J$ (or equivalently, for larger
$J$ (or equivalently, for larger ![]() $\phi$), as previously observed qualitatively in figures 1(a) and 1(b). Interestingly, Macaulay & Rognon (Reference Macaulay and Rognon2019) report a similar scaling law for inertial granular media,
$\phi$), as previously observed qualitatively in figures 1(a) and 1(b). Interestingly, Macaulay & Rognon (Reference Macaulay and Rognon2019) report a similar scaling law for inertial granular media,
as illustrated in figure 1(d). A priori, suspensions and inertial granular flows are different systems governed by their own dimensionless numbers, namely ![]() $J$ and
$J$ and ![]() $I$, which involve different physical mechanisms. However, as shown in figure 2(a), examination of the dilation laws
$I$, which involve different physical mechanisms. However, as shown in figure 2(a), examination of the dilation laws ![]() $\phi (J)$ and
$\phi (J)$ and ![]() $\phi (I)$ indicates that for such a frictional suspension,
$\phi (I)$ indicates that for such a frictional suspension,
with ![]() $\phi _c=0.81\pm 1\times 10^{-2}$, and for inertial granular media,
$\phi _c=0.81\pm 1\times 10^{-2}$, and for inertial granular media,
with ![]() $\phi _c=0.812\pm 1\times 10^{-3}$. By expressing
$\phi _c=0.812\pm 1\times 10^{-3}$. By expressing ![]() $J$ and
$J$ and ![]() $I$ as functions of
$I$ as functions of ![]() $\phi _c-\phi$, we expect that the diffusion coefficients of both the suspension, (3.1), and the inertial granular media, (3.2), follow the same scaling law
$\phi _c-\phi$, we expect that the diffusion coefficients of both the suspension, (3.1), and the inertial granular media, (3.2), follow the same scaling law ![]() $D_{{susp}} \sim D_{{gran}} \sim (\phi _c-\phi )^{-1/2}$. The striking result shown in figure 2(b) is that by plotting
$D_{{susp}} \sim D_{{gran}} \sim (\phi _c-\phi )^{-1/2}$. The striking result shown in figure 2(b) is that by plotting ![]() $D_{{susp}}$ and
$D_{{susp}}$ and ![]() $D_{{gran}}$ versus
$D_{{gran}}$ versus ![]() $\phi _c-\phi$, both sets of data collapse onto a single master curve. More precisely, the diffusion coefficients of suspensions and inertial granular media share not only the same exponent
$\phi _c-\phi$, both sets of data collapse onto a single master curve. More precisely, the diffusion coefficients of suspensions and inertial granular media share not only the same exponent ![]() $-1/2$, but also a very similar numerical prefactor, yielding
$-1/2$, but also a very similar numerical prefactor, yielding
Careful examination of figure 2(b) shows that ![]() $D_{{susp}}$ is slightly lower than
$D_{{susp}}$ is slightly lower than ![]() $D_{{gran}}$. (Individual fits of these two data sets are provided in the supplementary material available at https://doi.org/10.1017/jfm.2024.695.) This difference is actually surprisingly small given that the two data sets for suspensions and inertial granular media are obtained from different numerical codes. The near collapse of the data on a single power law indicates that shear-induced diffusion in granular systems is oblivious to the nature of the dissipation mechanism (viscous or inertial), and appears to be mainly geometrical, as set primarily by the particle solid fraction (see § 4 and Appendix D). This is a striking difference compared to other quantities related to dissipation, such as the viscosity or the shear stress, which, owing to stress additivity, collapse only when using a combination of
$D_{{gran}}$. (Individual fits of these two data sets are provided in the supplementary material available at https://doi.org/10.1017/jfm.2024.695.) This difference is actually surprisingly small given that the two data sets for suspensions and inertial granular media are obtained from different numerical codes. The near collapse of the data on a single power law indicates that shear-induced diffusion in granular systems is oblivious to the nature of the dissipation mechanism (viscous or inertial), and appears to be mainly geometrical, as set primarily by the particle solid fraction (see § 4 and Appendix D). This is a striking difference compared to other quantities related to dissipation, such as the viscosity or the shear stress, which, owing to stress additivity, collapse only when using a combination of ![]() $J$ and
$J$ and ![]() $I$ (Trulsson, Andreotti & Claudin Reference Trulsson, Andreotti and Claudin2012; Tapia et al. Reference Tapia, Ichihara, Pouliquen and Guazzelli2022).
$I$ (Trulsson, Andreotti & Claudin Reference Trulsson, Andreotti and Claudin2012; Tapia et al. Reference Tapia, Ichihara, Pouliquen and Guazzelli2022).

Figure 2. Unifying suspension and granular shear-induced self-diffusion. (a) Dilatancy laws ![]() $\phi (J)$ for suspensions (blue diamonds
$\phi (J)$ for suspensions (blue diamonds ![]() $\tilde {k}=10^{3}$, blue triangles
$\tilde {k}=10^{3}$, blue triangles ![]() $\tilde {k}=10^{4}$, blue circles
$\tilde {k}=10^{4}$, blue circles ![]() $\tilde {k}=10^{5}$, present study) and
$\tilde {k}=10^{5}$, present study) and ![]() $\phi (I)$ for dry inertial granular media (red squares, data from Da Cruz et al. Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005). Inset: same data plotting
$\phi (I)$ for dry inertial granular media (red squares, data from Da Cruz et al. Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005). Inset: same data plotting ![]() $\phi _c-\phi$ versus
$\phi _c-\phi$ versus ![]() $I$ and
$I$ and ![]() $J$. (b) Dimensionless particle diffusion coefficients
$J$. (b) Dimensionless particle diffusion coefficients ![]() $D/\dot {\gamma }d^2$ for suspensions and dry inertial granular media versus
$D/\dot {\gamma }d^2$ for suspensions and dry inertial granular media versus ![]() $\phi _c - \phi$ show a collapse on a single master curve. Uncertainties on
$\phi _c - \phi$ show a collapse on a single master curve. Uncertainties on ![]() $\phi _c$ are indicated by the horizontal error bars.
$\phi _c$ are indicated by the horizontal error bars.
To probe the physical origin of the above scaling law, we further analyse the particle trajectories to extract two kinematic quantities: the mean velocity fluctuation ![]() $\delta v = \langle v_{y,i}^2 \rangle ^{1/2}$ and its persistence time
$\delta v = \langle v_{y,i}^2 \rangle ^{1/2}$ and its persistence time ![]() $\varPsi$, which control the particle diffusive behaviour according to
$\varPsi$, which control the particle diffusive behaviour according to ![]() $D=\delta v^2\varPsi$ (Rognon & Macaulay Reference Rognon and Macaulay2021). These quantities are obtained following Olsson (Reference Olsson2010), DeGiuli et al. (Reference DeGiuli, Düring, Lerner and Wyart2015) and DeGiuli, McElwaine & Wyart (Reference DeGiuli, McElwaine and Wyart2016) by computing the autocorrelation function of the velocity fluctuations
$D=\delta v^2\varPsi$ (Rognon & Macaulay Reference Rognon and Macaulay2021). These quantities are obtained following Olsson (Reference Olsson2010), DeGiuli et al. (Reference DeGiuli, Düring, Lerner and Wyart2015) and DeGiuli, McElwaine & Wyart (Reference DeGiuli, McElwaine and Wyart2016) by computing the autocorrelation function of the velocity fluctuations ![]() $C(\tau )=\langle v_{y,i}(t_0)\,v_{y,i}(t_0+\tau ) \rangle$. Figure 3(a) evidences the scaling laws
$C(\tau )=\langle v_{y,i}(t_0)\,v_{y,i}(t_0+\tau ) \rangle$. Figure 3(a) evidences the scaling laws
obtained with our analysis for suspensions, and
for inertial granular media, as reported by Da Cruz et al. (Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005) for ![]() $\delta v(I)$ and by Macaulay & Rognon (Reference Macaulay and Rognon2019) for
$\delta v(I)$ and by Macaulay & Rognon (Reference Macaulay and Rognon2019) for ![]() $\varPsi (I)$; see also Dumont et al. (Reference Dumont, Bonneau, Salez, Raphael and Damman2023). As before, by virtue of the complementary scalings followed by the dilatancy laws in suspensions and granular media, these data sets are also found to collapse reasonably well when plotted versus
$\varPsi (I)$; see also Dumont et al. (Reference Dumont, Bonneau, Salez, Raphael and Damman2023). As before, by virtue of the complementary scalings followed by the dilatancy laws in suspensions and granular media, these data sets are also found to collapse reasonably well when plotted versus ![]() $\phi _c-\phi$, yielding the unified scaling laws
$\phi _c-\phi$, yielding the unified scaling laws
shown in figure 3(b).

Figure 3. Random walk analysis. (a) Normalized velocity fluctuations ![]() $\delta v/\dot {\gamma }d$ (filled symbols) and persistence time
$\delta v/\dot {\gamma }d$ (filled symbols) and persistence time ![]() $\varPsi \dot {\gamma }$ (open symbols) versus viscous number
$\varPsi \dot {\gamma }$ (open symbols) versus viscous number ![]() $J$ for suspensions (blue symbols, present study), and versus inertial number
$J$ for suspensions (blue symbols, present study), and versus inertial number ![]() $I$ for inertial granular media (red symbols, data from Da Cruz et al. (Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005) for
$I$ for inertial granular media (red symbols, data from Da Cruz et al. (Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005) for ![]() $\delta v(I)$ and from Macaulay & Rognon (Reference Macaulay and Rognon2019) for
$\delta v(I)$ and from Macaulay & Rognon (Reference Macaulay and Rognon2019) for ![]() $\varPsi (I)$). (b) Same data plotted versus
$\varPsi (I)$). (b) Same data plotted versus ![]() $\phi _c-\phi$. (c) Same symbols as figure 2.
$\phi _c-\phi$. (c) Same symbols as figure 2.
These scaling laws point out the random walk process underpinning the grains’ diffusive behaviour: as shown in figure 3(c), grains take steps in random directions after a characteristic displacement ![]() $\ell = \delta v \varPsi$. Individual fits yield
$\ell = \delta v \varPsi$. Individual fits yield ![]() $\ell \approx 0.15 d$ for inertial grains (red dashed line) and
$\ell \approx 0.15 d$ for inertial grains (red dashed line) and ![]() $0.09d$ for suspensions (blue dashed line). Remarkably, the step size
$0.09d$ for suspensions (blue dashed line). Remarkably, the step size ![]() $\ell$, typically a small fraction of a grain size, is independent of the solid fraction
$\ell$, typically a small fraction of a grain size, is independent of the solid fraction ![]() $\phi$, and weakly sensitive whether grains are immersed in a viscous fluid or not. By contrast, the step frequency
$\phi$, and weakly sensitive whether grains are immersed in a viscous fluid or not. By contrast, the step frequency ![]() $\varPsi ^{-1}\sim (\phi _c-\phi )^{-1/2}$ increases when increasing the solid fraction, which is the sole driver of the increase in the normalized diffusivity captured in (3.1). This scenario is further confirmed by the inset of figure 1(c), which shows that the mean square displacements collapse onto a single curve
$\varPsi ^{-1}\sim (\phi _c-\phi )^{-1/2}$ increases when increasing the solid fraction, which is the sole driver of the increase in the normalized diffusivity captured in (3.1). This scenario is further confirmed by the inset of figure 1(c), which shows that the mean square displacements collapse onto a single curve ![]() $\varDelta _y^2(t/\varPsi )/d^2$, once time is normalized by the step frequency
$\varDelta _y^2(t/\varPsi )/d^2$, once time is normalized by the step frequency ![]() $\varPsi ^{-1}$. For all viscous numbers investigated (or equivalent solid fractions), the transition between ballistic and diffusive regimes occurs at time
$\varPsi ^{-1}$. For all viscous numbers investigated (or equivalent solid fractions), the transition between ballistic and diffusive regimes occurs at time ![]() $t/\varPsi \approx {O}(1)$ and for a typical constant mean square displacement
$t/\varPsi \approx {O}(1)$ and for a typical constant mean square displacement ![]() $\varDelta _y^2/d^2 \approx 0.02$, close to the square of one elementary step of the random walk
$\varDelta _y^2/d^2 \approx 0.02$, close to the square of one elementary step of the random walk ![]() $\ell ^2/d^2 \approx 0.017$. Note that in the kinetic theory for granular gases, the diffusion coefficient is often plotted as a function of the square root of the granular temperature, equivalent here to the velocity fluctuations
$\ell ^2/d^2 \approx 0.017$. Note that in the kinetic theory for granular gases, the diffusion coefficient is often plotted as a function of the square root of the granular temperature, equivalent here to the velocity fluctuations ![]() $\delta v$. As shown in Appendix D, we find that indeed
$\delta v$. As shown in Appendix D, we find that indeed ![]() $D$ scales with
$D$ scales with ![]() $\sqrt {T}$, but the data obtained from suspensions and dry granular media do not collapse onto a single curve. By contrast, the complete dimensional scaling, introducing also either
$\sqrt {T}$, but the data obtained from suspensions and dry granular media do not collapse onto a single curve. By contrast, the complete dimensional scaling, introducing also either ![]() $\ell$ the step length (such that
$\ell$ the step length (such that ![]() $D= \delta v \ell$) or equivalently
$D= \delta v \ell$) or equivalently ![]() $\varPsi$ the persistence time (such that
$\varPsi$ the persistence time (such that ![]() $D= \delta v^2 \varPsi$), provides a better match between both data sets.
$D= \delta v^2 \varPsi$), provides a better match between both data sets.
4. Discussion
The unified framework introduced here allows us to better understand and predict the process of shear-induced self-diffusion in both suspensions and dry inertial granular flows. Results from two-dimensional simulations highlight scaling laws for the diffusivity as a function of the flow property, grain diameter and solid fraction, and provide a physical rationale for its origin in term of a granular random walk. Of fundamental importance is the finding of a unique scaling law for ![]() $D \approx 0.027 (\phi _c-\phi )^{-1/2}\dot {\gamma } d^2$ that applies for both suspensions and inertial granular media. We also show that this scaling stems from a specific random walk process having a constant elementary step length
$D \approx 0.027 (\phi _c-\phi )^{-1/2}\dot {\gamma } d^2$ that applies for both suspensions and inertial granular media. We also show that this scaling stems from a specific random walk process having a constant elementary step length ![]() $\ell /d$ driven at frequency
$\ell /d$ driven at frequency ![]() $\varPsi ^{-1} \sim \dot {\gamma }(\phi _c-\phi )^{-1/2}$, which increases with the solid fraction.
$\varPsi ^{-1} \sim \dot {\gamma }(\phi _c-\phi )^{-1/2}$, which increases with the solid fraction.
These results call for several comments. The proposed scaling law for the particle diffusion coefficient diverges at jamming, i.e. when ![]() $J\to 0$ or
$J\to 0$ or ![]() $I \to 0$ (equivalently, when
$I \to 0$ (equivalently, when ![]() $\phi \to \phi _c$). As it is unlikely that particles can experience an infinite displacement over a small but finite strain, we anticipate that this scaling should ultimately break down and saturate when
$\phi \to \phi _c$). As it is unlikely that particles can experience an infinite displacement over a small but finite strain, we anticipate that this scaling should ultimately break down and saturate when ![]() $\phi \to \phi _c$. For a finite-size system, a saturation of the particle diffusion coefficient is expected when correlated structures in the flow start to reach the system size, as observed with granular flows in Kharel & Rognon (Reference Kharel and Rognon2017).
$\phi \to \phi _c$. For a finite-size system, a saturation of the particle diffusion coefficient is expected when correlated structures in the flow start to reach the system size, as observed with granular flows in Kharel & Rognon (Reference Kharel and Rognon2017).
Some caution is also required as the scaling laws presented here were obtained in a uniform shear flow (other non-uniform flows could lead to different scaling relations). These scaling laws were also drawn from two-dimensional numerical simulations, although previous numerical works show that exponents characterizing the divergence of macroscopic quantities are unchanged for simulations performed in two and three dimensions (DeGiuli et al. Reference DeGiuli, Düring, Lerner and Wyart2015).
An important remaining question is the role played by particle friction. Simulations here were performed with a particle friction coefficient ![]() $\mu _p=0.5$. However, other studies have shown that changes in the particle friction coefficient can affect scaling exponents of velocity fluctuations and persistence time (Trulsson, DeGiuli & Wyart Reference Trulsson, DeGiuli and Wyart2017). Whether these changes can alter the unified description put forth in the present study still needs to be determined. For instance, the scaling analysis proposed in Olsson (Reference Olsson2010) for frictionless particles suggests that in this case,
$\mu _p=0.5$. However, other studies have shown that changes in the particle friction coefficient can affect scaling exponents of velocity fluctuations and persistence time (Trulsson, DeGiuli & Wyart Reference Trulsson, DeGiuli and Wyart2017). Whether these changes can alter the unified description put forth in the present study still needs to be determined. For instance, the scaling analysis proposed in Olsson (Reference Olsson2010) for frictionless particles suggests that in this case, ![]() $D\sim (\phi _c-\phi )^{-0.8}$. (Olsson (Reference Olsson2010) identified that the particle diffusion coefficient for frictionless particles in the hard core limit obeys the scaling function
$D\sim (\phi _c-\phi )^{-0.8}$. (Olsson (Reference Olsson2010) identified that the particle diffusion coefficient for frictionless particles in the hard core limit obeys the scaling function ![]() $D/\dot {\gamma }^q \sim (\delta \phi / \dot {\gamma }^{1/(\beta +\varDelta )})^{-x}$, where
$D/\dot {\gamma }^q \sim (\delta \phi / \dot {\gamma }^{1/(\beta +\varDelta )})^{-x}$, where ![]() $\delta \phi = \phi -\phi _c$. Using that
$\delta \phi = \phi -\phi _c$. Using that ![]() $D \sim \dot {\gamma }$, one expects
$D \sim \dot {\gamma }$, one expects ![]() $D\sim \delta \phi ^{-0.8}$ as
$D\sim \delta \phi ^{-0.8}$ as ![]() $x$ must be equal to
$x$ must be equal to ![]() $(1-q)(\beta +\varDelta )$, with
$(1-q)(\beta +\varDelta )$, with ![]() $q\approx 0.78$ and
$q\approx 0.78$ and ![]() $1/(\beta +\varDelta ) \approx 0.275$.)
$1/(\beta +\varDelta ) \approx 0.275$.)
Our analysis differs from the recent approaches to unify rheological flow rules of suspensions and inertial granular media using the dimensionless viscous-inertial number ![]() $K=J+ \alpha I^2$ (Trulsson et al. Reference Trulsson, Andreotti and Claudin2012; Ness & Sun Reference Ness and Sun2015; Tapia et al. Reference Tapia, Ichihara, Pouliquen and Guazzelli2022). The viscous-inertial number is built from the idea of stress additivity, and gives the adjustable dimensionless prefactor
$K=J+ \alpha I^2$ (Trulsson et al. Reference Trulsson, Andreotti and Claudin2012; Ness & Sun Reference Ness and Sun2015; Tapia et al. Reference Tapia, Ichihara, Pouliquen and Guazzelli2022). The viscous-inertial number is built from the idea of stress additivity, and gives the adjustable dimensionless prefactor ![]() $\alpha$ an important role since it allows us to accommodate the difference in magnitude of the dissipation mechanisms at play in suspensions and granular media. Stress additivity seems to be well verified (Trulsson et al. Reference Trulsson, Andreotti and Claudin2012; Ness & Sun Reference Ness and Sun2015; Tapia et al. Reference Tapia, Ichihara, Pouliquen and Guazzelli2022) – although not always (Otsuki & Hayakawa Reference Otsuki and Hayakawa2009; Vågberg, Olsson & Teitel Reference Vågberg, Olsson and Teitel2016; Ness, Seto & Mari Reference Ness, Seto and Mari2022) – thereby yielding a good collapse of quantities involving dissipation, like the effective friction or the shear stress. However, unlike the inertial number
$\alpha$ an important role since it allows us to accommodate the difference in magnitude of the dissipation mechanisms at play in suspensions and granular media. Stress additivity seems to be well verified (Trulsson et al. Reference Trulsson, Andreotti and Claudin2012; Ness & Sun Reference Ness and Sun2015; Tapia et al. Reference Tapia, Ichihara, Pouliquen and Guazzelli2022) – although not always (Otsuki & Hayakawa Reference Otsuki and Hayakawa2009; Vågberg, Olsson & Teitel Reference Vågberg, Olsson and Teitel2016; Ness, Seto & Mari Reference Ness, Seto and Mari2022) – thereby yielding a good collapse of quantities involving dissipation, like the effective friction or the shear stress. However, unlike the inertial number ![]() $I$ for inertial granular media and the viscous number
$I$ for inertial granular media and the viscous number ![]() $J$ for viscous suspensions, the viscous-inertial number is not a direct outcome of dimensional analysis. There is therefore no reason to expect that all observables are functions of
$J$ for viscous suspensions, the viscous-inertial number is not a direct outcome of dimensional analysis. There is therefore no reason to expect that all observables are functions of ![]() $K$. It particular, we do not expect that stress additivity has any relevance for a microscopic transport quantity such as
$K$. It particular, we do not expect that stress additivity has any relevance for a microscopic transport quantity such as ![]() $D$, and therefore that
$D$, and therefore that ![]() $D$ is a function of
$D$ is a function of ![]() $K$. That a good collapse is readily found by plotting
$K$. That a good collapse is readily found by plotting ![]() $D$ versus
$D$ versus ![]() $(\phi _c-\phi )^{-1/2}$ rather shows that self-diffusion is primarily set by steric, geometrical effects, and is oblivious to the dissipation mechanism. The idea that transport properties in granular media are purely kinematic, while stresses depend on the nature of the interactions, was also put forth in Maiti & Heussinger (Reference Maiti and Heussinger2014). Nonetheless, if we further assume stress additivity, then
$(\phi _c-\phi )^{-1/2}$ rather shows that self-diffusion is primarily set by steric, geometrical effects, and is oblivious to the dissipation mechanism. The idea that transport properties in granular media are purely kinematic, while stresses depend on the nature of the interactions, was also put forth in Maiti & Heussinger (Reference Maiti and Heussinger2014). Nonetheless, if we further assume stress additivity, then ![]() $(\phi _c-\phi )$ is itself a function of
$(\phi _c-\phi )$ is itself a function of ![]() $K$, and we therefore expect to be able to collapse our diffusion coefficient data with
$K$, and we therefore expect to be able to collapse our diffusion coefficient data with ![]() $K$. As shown in Appendix C, we can indeed carefully adjust the value of
$K$. As shown in Appendix C, we can indeed carefully adjust the value of ![]() $\alpha$ to find a good collapse for both suspensions and granular media, which we interpret as merely a validation of the hypothesis of stress additivity. Finally, note that the behaviour of the collective shear-induced diffusion coefficient, which drives particle migration in inhomogeneous systems, is expected to be different. The latter quantity describes the response of the system to particles stress gradient (osmotic compressibility; Leshansky & Brady Reference Leshansky and Brady2005), and should therefore depend on the nature of the dissipation mechanism. Nonetheless, establishing the link between self and collective diffusivities in the dense regime would be an interesting problem to investigate in future studies.
$\alpha$ to find a good collapse for both suspensions and granular media, which we interpret as merely a validation of the hypothesis of stress additivity. Finally, note that the behaviour of the collective shear-induced diffusion coefficient, which drives particle migration in inhomogeneous systems, is expected to be different. The latter quantity describes the response of the system to particles stress gradient (osmotic compressibility; Leshansky & Brady Reference Leshansky and Brady2005), and should therefore depend on the nature of the dissipation mechanism. Nonetheless, establishing the link between self and collective diffusivities in the dense regime would be an interesting problem to investigate in future studies.
To conclude, we can draw some interesting perspectives on mixing granular and suspension flows, which represents a considerable challenge in industry. For such athermal systems, particle diffusion is a self-induced process prescribed by the flow itself, as opposed to standard mixing problems where advection and molecular diffusion are independent. Having ![]() $D\sim f(\phi )\,\dot {\gamma }d^2$ from (3.5), one obtains a Péclet number
$D\sim f(\phi )\,\dot {\gamma }d^2$ from (3.5), one obtains a Péclet number ![]() $Pe \sim \dot {\gamma } d^2/D \sim 1/f(\phi )$, which characterizes the mixing process, that is independent of the shear rate (under volume-imposed conditions) (Souzy et al. Reference Souzy, Zaier, Lhuissier, Le Borgne and Metzger2018; Villermaux Reference Villermaux2019). Mixing dense granular media must then in essence be a purely kinematic process: the state of the mixture should depend not on the rate at which the substrate is deformed, only on the magnitude of the deformation – an interesting and quite relevant problem that certainly deserves further investigations.
$Pe \sim \dot {\gamma } d^2/D \sim 1/f(\phi )$, which characterizes the mixing process, that is independent of the shear rate (under volume-imposed conditions) (Souzy et al. Reference Souzy, Zaier, Lhuissier, Le Borgne and Metzger2018; Villermaux Reference Villermaux2019). Mixing dense granular media must then in essence be a purely kinematic process: the state of the mixture should depend not on the rate at which the substrate is deformed, only on the magnitude of the deformation – an interesting and quite relevant problem that certainly deserves further investigations.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2024.695.
Acknowledgements
We thank O. Pouliquen, M. Wyart and E. Villermaux for discussions.
Funding
This work was supported by ANR ScienceFriction (ANR-18-CE30-0024), and ARC Wear (DP200101927).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Simulating plane shear of dense suspensions
The material is a suspension of non-Brownian grains in a fluid of viscosity ![]() $\eta$ in the Stokes regime. The system is quasi-two-dimensional to avoid prohibitive simulation times, and comprises
$\eta$ in the Stokes regime. The system is quasi-two-dimensional to avoid prohibitive simulation times, and comprises ![]() $N$ spherical grains set on the
$N$ spherical grains set on the ![]() $xy$ plane, using a bidisperse size distribution with diameters
$xy$ plane, using a bidisperse size distribution with diameters ![]() $d$ and
$d$ and ![]() $1.4d$, mixed in equal volume. The mass of the grains is set to zero to clear inertia and focus on an over-damped dynamics. The equations of motion are obtained by imposing force and torque balances on each particle. Force balance on particle
$1.4d$, mixed in equal volume. The mass of the grains is set to zero to clear inertia and focus on an over-damped dynamics. The equations of motion are obtained by imposing force and torque balances on each particle. Force balance on particle ![]() $i$ is
$i$ is ![]() ${\boldsymbol {f\!}}_{{d},i} + {\boldsymbol {f\!}}_{{l},i} + {\boldsymbol {f\!}}_{{c},i} = 0$. Here, we omit torque balance, which involves the same interactions (Mari et al. Reference Mari, Seto, Morris and Denn2014). In the latter equation,
${\boldsymbol {f\!}}_{{d},i} + {\boldsymbol {f\!}}_{{l},i} + {\boldsymbol {f\!}}_{{c},i} = 0$. Here, we omit torque balance, which involves the same interactions (Mari et al. Reference Mari, Seto, Morris and Denn2014). In the latter equation, ![]() ${\boldsymbol {f\!}}_{{d},i} = - 3{\rm \pi} \eta d_i (\boldsymbol {v_i}-\boldsymbol {v}_{\infty }(y_i) )$ is the Stokes drag, with
${\boldsymbol {f\!}}_{{d},i} = - 3{\rm \pi} \eta d_i (\boldsymbol {v_i}-\boldsymbol {v}_{\infty }(y_i) )$ is the Stokes drag, with ![]() $r_i$ the radius of the particle
$r_i$ the radius of the particle ![]() $i$,
$i$, ![]() $\boldsymbol {v}_i$ its velocity, and
$\boldsymbol {v}_i$ its velocity, and ![]() $\boldsymbol {v}_\infty (y_i) = (\dot {\gamma } y_i,0)$ the assumed background fluid velocity. The force
$\boldsymbol {v}_\infty (y_i) = (\dot {\gamma } y_i,0)$ the assumed background fluid velocity. The force ![]() $\boldsymbol {f\!}_{{l},i}$ is the resulting force of all pairwise lubrication interactions involving particle
$\boldsymbol {f\!}_{{l},i}$ is the resulting force of all pairwise lubrication interactions involving particle ![]() $i$. We include the dominant modes of lubrication (the ‘squeeze’, ‘shear’ and ‘pump’ modes; Ball & Melrose Reference Ball and Melrose1997). These provide normal and tangential forces which magnitude depend on the dimensionless gap between particles
$i$. We include the dominant modes of lubrication (the ‘squeeze’, ‘shear’ and ‘pump’ modes; Ball & Melrose Reference Ball and Melrose1997). These provide normal and tangential forces which magnitude depend on the dimensionless gap between particles ![]() $i$ and
$i$ and ![]() $j$ located at positions
$j$ located at positions ![]() $\boldsymbol {r}_{i}$ and
$\boldsymbol {r}_{i}$ and ![]() $\boldsymbol {r}_{j}$,
$\boldsymbol {r}_{j}$, ![]() $h_{ij} = 4 |\boldsymbol {r}_j - \boldsymbol {r}_i|/(d_i+d_j) - 2$, as
$h_{ij} = 4 |\boldsymbol {r}_j - \boldsymbol {r}_i|/(d_i+d_j) - 2$, as ![]() $1/(h_{ij}+\delta )$ and
$1/(h_{ij}+\delta )$ and ![]() $\log (h_{ij}+\delta )$, respectively. The regularization length
$\log (h_{ij}+\delta )$, respectively. The regularization length ![]() $\delta = 10^{-2}$ mimics the presence of particle roughness on this scale that allows for contact to happen despite lubrication. The force
$\delta = 10^{-2}$ mimics the presence of particle roughness on this scale that allows for contact to happen despite lubrication. The force ![]() $\boldsymbol {f\!}_{{c},i}$ is the resulting contact force on
$\boldsymbol {f\!}_{{c},i}$ is the resulting contact force on ![]() $i$. Contact forces involve normal and frictional tangential components, both modelled with spring and dashpot (Cundall & Strack Reference Cundall and Strack1979). Contacts follow Coulomb's law with a friction coefficient
$i$. Contact forces involve normal and frictional tangential components, both modelled with spring and dashpot (Cundall & Strack Reference Cundall and Strack1979). Contacts follow Coulomb's law with a friction coefficient ![]() $0.5$. The ratio of tangential to normal stiffnesses is set as
$0.5$. The ratio of tangential to normal stiffnesses is set as ![]() $k_{t}/k_{n} = 0.5$, and the dashpot resistances are set to match the normal and tangential resistance of lubrication right at contact (i.e. for
$k_{t}/k_{n} = 0.5$, and the dashpot resistances are set to match the normal and tangential resistance of lubrication right at contact (i.e. for ![]() $h_{ij} = 0$). The normal stiffness is varied as
$h_{ij} = 0$). The normal stiffness is varied as ![]() $k_n \in [10^3,10^5]Pd$ to show that our results are representative of the hard particle limit. The full detail of the interactions and numerical scheme are presented in Mari et al. (Reference Mari, Seto, Morris and Denn2014).
$k_n \in [10^3,10^5]Pd$ to show that our results are representative of the hard particle limit. The full detail of the interactions and numerical scheme are presented in Mari et al. (Reference Mari, Seto, Morris and Denn2014).
The suspension is sheared between two rough boundaries, which simultaneously prescribe a constant shear rate ![]() $\dot {\gamma }$ and a constant normal stress
$\dot {\gamma }$ and a constant normal stress ![]() $P$. Both boundaries are made of grains similar to the flowing grains, but moving as a rigid body: grains forming a boundary share the same velocity in the
$P$. Both boundaries are made of grains similar to the flowing grains, but moving as a rigid body: grains forming a boundary share the same velocity in the ![]() $x$ and
$x$ and ![]() $y$ directions, and have no rotation. To prescribe the shear rate, one boundary is kept fixed and the other moves along the
$y$ directions, and have no rotation. To prescribe the shear rate, one boundary is kept fixed and the other moves along the ![]() $x$ direction at speed
$x$ direction at speed ![]() $V(t) = \dot {\gamma }H(t)$, where
$V(t) = \dot {\gamma }H(t)$, where ![]() $H$ is the mean distance between the two boundaries. The system is periodic in the
$H$ is the mean distance between the two boundaries. The system is periodic in the ![]() $x$ direction. To keep the normal stress
$x$ direction. To keep the normal stress ![]() $P$ constant, the moving boundary can also move in the
$P$ constant, the moving boundary can also move in the ![]() $y$ direction. Again using linearity of dashpot and lubrication forces in velocities, the
$y$ direction. Again using linearity of dashpot and lubrication forces in velocities, the ![]() $y$ velocity component is set at every time step so that the sum of all contact and hydrodynamic forces that particles in the moving wall exert on the particles in the suspension is
$y$ velocity component is set at every time step so that the sum of all contact and hydrodynamic forces that particles in the moving wall exert on the particles in the suspension is ![]() $PL_x$, with
$PL_x$, with ![]() $L_x$ the wall length (Athani et al. Reference Athani, Metzger, Forterre and Mari2022). The motion along
$L_x$ the wall length (Athani et al. Reference Athani, Metzger, Forterre and Mari2022). The motion along ![]() $y$ of the wall implies dilation or contraction of the sheared material. We checked that the steady flow solid fraction
$y$ of the wall implies dilation or contraction of the sheared material. We checked that the steady flow solid fraction ![]() $\phi$ is independent on the initial solid fraction
$\phi$ is independent on the initial solid fraction ![]() $\phi _{i}$, ruling out potential micro-structural memory effect. The results were obtained with a system comprised of
$\phi _{i}$, ruling out potential micro-structural memory effect. The results were obtained with a system comprised of ![]() $N=1000$ grains. We checked that systems comprised of
$N=1000$ grains. We checked that systems comprised of ![]() $N=500$ and
$N=500$ and ![]() $1500$ yielded similar diffusivity, velocity fluctuations and time persistence.
$1500$ yielded similar diffusivity, velocity fluctuations and time persistence.
Appendix B. Fitting procedure, parameters and uncertainty
Equations (3.1), (3.2), (3.5)–(3.8) are obtained by fitting the numerical data using a power law of the form ![]() $g(x) = ax^b$ and by letting both
$g(x) = ax^b$ and by letting both ![]() $a$ and
$a$ and ![]() $b$ be free parameters. Fits are performed in the log-log space, effectively fitting the log of the quantities
$b$ be free parameters. Fits are performed in the log-log space, effectively fitting the log of the quantities ![]() $\log (g(\log (x)))$ by an affine function
$\log (g(\log (x)))$ by an affine function ![]() $\log (a)+\log (b)\,x$. For the sake of clarity, the best-fit exponents
$\log (a)+\log (b)\,x$. For the sake of clarity, the best-fit exponents ![]() $b$ were rounded to the nearest fractional exponent (within their respective standard error). Table 1 summarizes the values of the best-fit parameters and their respective standard errors.
$b$ were rounded to the nearest fractional exponent (within their respective standard error). Table 1 summarizes the values of the best-fit parameters and their respective standard errors.
Table 1. Best fit parameters and errors bars obtained when fitting (3.1), (3.2), (3.5)–(3.8) by ![]() $g(x) = ax^b$.
$g(x) = ax^b$.

The dilatancy laws (3.3) and (3.4) were fitted by a function ![]() $\phi (x) = \phi _c - a x^b$. First, the value of
$\phi (x) = \phi _c - a x^b$. First, the value of ![]() $\phi _c$ is obtained by adjusting
$\phi _c$ is obtained by adjusting ![]() $\phi _c$ until the data for
$\phi _c$ until the data for ![]() $\phi -\phi _c$ best align along a straight line in log-log scales. Then
$\phi -\phi _c$ best align along a straight line in log-log scales. Then ![]() $\phi _c$ is fixed,
$\phi _c$ is fixed, ![]() $\phi -\phi _c$ is fitted by the power law
$\phi -\phi _c$ is fitted by the power law ![]() $a x^b$ by letting both
$a x^b$ by letting both ![]() $a$ and
$a$ and ![]() $b$ be free parameters. Finally, the error on
$b$ be free parameters. Finally, the error on ![]() $\phi _c$ is estimated by fitting again
$\phi _c$ is estimated by fitting again ![]() $\phi (x) = \phi _c - a x^b$ by letting
$\phi (x) = \phi _c - a x^b$ by letting ![]() $\phi _c$ be a free parameter but fixing
$\phi _c$ be a free parameter but fixing ![]() $a$ and
$a$ and ![]() $b$. The difference between the initially estimated value of
$b$. The difference between the initially estimated value of ![]() $\phi _c$ and that returned by this last fit provides an estimate of the error on
$\phi _c$ and that returned by this last fit provides an estimate of the error on ![]() $\phi _c$. The error bar on
$\phi _c$. The error bar on ![]() $\phi _c$ is represented in figures 2(b) and 3(b). Table 2 summarizes the values of the best-fit parameters and their respective standard errors.
$\phi _c$ is represented in figures 2(b) and 3(b). Table 2 summarizes the values of the best-fit parameters and their respective standard errors.
Appendix C. Unifying suspension and granular self-diffusion using  $K=J+\alpha I^2$
$K=J+\alpha I^2$
In the spirit of Trulsson et al. (Reference Trulsson, Andreotti and Claudin2012) and Tapia et al. (Reference Tapia, Ichihara, Pouliquen and Guazzelli2022), figures 4(a) and 4(b) revisit the data shown in figures 1(d) and 3(a). Here, self-diffusion coefficients, velocity fluctuations and persistence times are plotted versus the dimensionless number ![]() $K=J+\alpha I^2$, where
$K=J+\alpha I^2$, where ![]() $\alpha$ is a numerical fitting factor. Here too, shear-induced self-diffusion coefficients from suspension and inertial granular media are found to collapse on a single curve
$\alpha$ is a numerical fitting factor. Here too, shear-induced self-diffusion coefficients from suspension and inertial granular media are found to collapse on a single curve ![]() $D/ \dot {\gamma }d^2=0.027K^{-{1}/{4}}$, with
$D/ \dot {\gamma }d^2=0.027K^{-{1}/{4}}$, with ![]() $\alpha =0.025$. Similarly, the normalized velocity fluctuations follow
$\alpha =0.025$. Similarly, the normalized velocity fluctuations follow ![]() $\delta v/\dot {\gamma }d^2=0.25K^{-{1}/{4}}$ and persistence time
$\delta v/\dot {\gamma }d^2=0.25K^{-{1}/{4}}$ and persistence time ![]() $\varPsi \dot {\gamma }=0.44K^{{1}/{4}}$, with
$\varPsi \dot {\gamma }=0.44K^{{1}/{4}}$, with ![]() $\alpha =0.4$.
$\alpha =0.4$.

Figure 4. Unifying suspension and granular shear-induced self-diffusion using ![]() $K=J+\alpha I^2$. (a) Normalized shear-induced self-diffusion coefficients from figure 1(d) plotted versus
$K=J+\alpha I^2$. (a) Normalized shear-induced self-diffusion coefficients from figure 1(d) plotted versus ![]() $K=J+0.025I^2$. (b) Normalized velocity fluctuations
$K=J+0.025I^2$. (b) Normalized velocity fluctuations ![]() $\delta v/\dot {\gamma } d$ (filled symbols) and persistence times
$\delta v/\dot {\gamma } d$ (filled symbols) and persistence times ![]() $\varPsi \dot {\gamma }$ (open symbols) from figure 3(a) plotted versus
$\varPsi \dot {\gamma }$ (open symbols) from figure 3(a) plotted versus ![]() $K=J+0.4I^2$.
$K=J+0.4I^2$.
Appendix D. Scaling of  $D$ with the granular temperature
$D$ with the granular temperature
In line with the picture of a random walk, the diffusion coefficient should follow ![]() $D= \delta v^2 \varPsi = \delta v \ell$, where
$D= \delta v^2 \varPsi = \delta v \ell$, where ![]() $\delta v= \sqrt {T}$ are the velocity fluctuations, by definition equal to the square root of the granular temperature (in the kinetic theory of granular gases, e.g. Artoni et al. Reference Artoni, Larcher, Jenkins and Richard2021),
$\delta v= \sqrt {T}$ are the velocity fluctuations, by definition equal to the square root of the granular temperature (in the kinetic theory of granular gases, e.g. Artoni et al. Reference Artoni, Larcher, Jenkins and Richard2021), ![]() $\varPsi$ is the persistence time, and
$\varPsi$ is the persistence time, and ![]() $\ell =\delta v \varPsi$ is the step length. As a result, we find that
$\ell =\delta v \varPsi$ is the step length. As a result, we find that ![]() $D$ scales with
$D$ scales with ![]() $\sqrt {T}=\delta v$, but the data obtained from suspensions and dry granular media do not collapse onto a single curve; see figure 5(a). By contrast, plotting
$\sqrt {T}=\delta v$, but the data obtained from suspensions and dry granular media do not collapse onto a single curve; see figure 5(a). By contrast, plotting ![]() $D$ versus
$D$ versus ![]() $\delta v \ell =\delta v^2 \varPsi$, which accounts for the difference in
$\delta v \ell =\delta v^2 \varPsi$, which accounts for the difference in ![]() $\ell$ (or
$\ell$ (or ![]() $\varPsi$) in suspensions and inertial granular media, provides a full collapse of the data, see figure 5(b). These results show that the description of the shear induced self-diffusion coefficient cannot be unified solely using the square root of the granular temperature, one must account for the full dimensional scaling, introducing also either
$\varPsi$) in suspensions and inertial granular media, provides a full collapse of the data, see figure 5(b). These results show that the description of the shear induced self-diffusion coefficient cannot be unified solely using the square root of the granular temperature, one must account for the full dimensional scaling, introducing also either ![]() $\ell$ the step length (such that
$\ell$ the step length (such that ![]() $D= \delta v \ell$) or equivalently
$D= \delta v \ell$) or equivalently ![]() $\varPsi$ the persistence time (such that
$\varPsi$ the persistence time (such that ![]() $D= \delta v^2 \varPsi$).
$D= \delta v^2 \varPsi$).

Figure 5. Diffusion coefficient and granular temperature. (a) Normalized shear induced self-diffusion coefficient ![]() $D/\dot {\gamma }d^2$ versus square root of the granular temperature
$D/\dot {\gamma }d^2$ versus square root of the granular temperature ![]() $\sqrt {T}/\dot {\gamma }d=\delta v/\dot {\gamma }d$. (b) Same data versus
$\sqrt {T}/\dot {\gamma }d=\delta v/\dot {\gamma }d$. (b) Same data versus ![]() $\delta v^2 \varPsi /\dot {\gamma }d^2 \equiv \delta v \ell /\dot {\gamma }d^2$.
$\delta v^2 \varPsi /\dot {\gamma }d^2 \equiv \delta v \ell /\dot {\gamma }d^2$.