Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T01:19:17.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent Rayleigh–Bénard convection in non-colloidal suspensions

Published online by Cambridge University Press:  13 July 2022

Andreas D. Demou Open the ORCID record for Andreas D. Demou [Opens in a new window] ,
Mehdi Niazi Ardekani Open the ORCID record for Mehdi Niazi Ardekani [Opens in a new window] ,
Parisa Mirbod Open the ORCID record for Parisa Mirbod [Opens in a new window]  and
Luca Brandt Open the ORCID record for Luca Brandt [Opens in a new window]
Andreas D. Demou*
Affiliation:
Computation-based Science and Technology Research Center, The Cyprus Institute, 20 Kavafi Street, Nicosia 2121, Cyprus
Mehdi Niazi Ardekani
Affiliation:
FLOW, Department of Engineering Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
Parisa Mirbod
Affiliation:
Department of Mechanical and Industrial Engineering, University of Illinois, Chicago, IL 60607, USA
Luca Brandt
Affiliation:
FLOW, Department of Engineering Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden Department of Energy and Process Engineering, Norwegian University of Science and Technology (NTNU), NO-7491 Trondheim, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

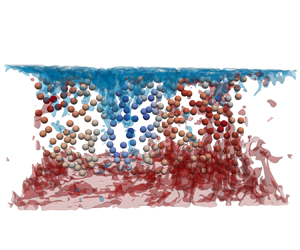
This study presents direct numerical simulations of turbulent Rayleigh–Bénard convection in non-colloidal suspensions, with special focus on the heat transfer modifications in the flow. Adopting a Rayleigh number of $10^8$ and Prandtl number of 7, parametric investigations of the particle volume fraction $0\leq \varPhi \leq 40\,\%$ and particle diameter $1/20\leq d^*_p\leq 1/10$ with respect to the cavity height, are carried out. The particles are neutrally buoyant, rigid spheres with physical properties that match the fluid phase. Up to $\varPhi =25\,\%$, the Nusselt number increases weakly but steadily, mainly due to the increased thermal agitation that overcomes the decreased kinetic energy of the flow. Beyond $\varPhi =30\,\%$, the Nusselt number exhibits a substantial drop, down to approximately 1/3 of the single-phase value. This decrease is attributed to the dense particle layering in the near-wall region, confirmed by the time-averaged local volume fraction. The dense particle layer reduces the convection in the near-wall region and negates the formation of any coherent structures within one particle diameter from the wall. Significant differences between $\varPhi \leq 30\,\%$ and 40 % are observed in all statistical quantities, including heat transfer and turbulent kinetic energy budgets, and two-point correlations. Special attention is also given to the role of particle rotation, which is shown to contribute to maintaining high heat transfer rates in moderate volume fractions. Furthermore, decreasing the particle size promotes the particle layering next to the wall, inducing a similar heat transfer reduction as in the highest particle volume fraction case.

JFM classification

Complex Fluids: Suspensions Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 945 , 25 August 2022 , A6
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E., Araujo, F.F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503.CrossRefGoogle Scholar
Ardekani, M.N., Abouali, O., Picano, F. & Brandt, L. 2018 a Heat transfer in laminar Couette flow laden with rigid spherical particles. J. Fluid Mech. 834, 308–334.CrossRefGoogle Scholar
Ardekani, M.N., Al Asmar, L., Picano, F. & Brandt, L. 2018 b Numerical study of heat transfer in laminar and turbulent pipe flow with finite-size spherical particles. Intl J. Heat Fluid Flow 71, 189–199.CrossRefGoogle Scholar
Ardekani, M.N., Costa, P., Breugem, W.P. & Brandt, L. 2016 Numerical study of the sedimentation of spheroidal particles. Intl J. Multiphase Flow 87, 16–34.CrossRefGoogle Scholar
Boussinesq, J. 1903 Théorie analytique de la chaleur mise en harmonic avec la thermodynamique et avec la théorie mécanique de la lumière: Tome I-[II]…, vol. 2. Gauthier-Villars.Google Scholar
Brandt, L. & Coletti, F. 2022 Particle-laden turbulence: progress and perspectives. Annu. Rev. Fluid Mech. 54, 159–189.CrossRefGoogle Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3), 242–251.CrossRefGoogle Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Busse, F.H. 1970 Differential rotation in stellar convection zones. Astrophys. J. 159, 629.CrossRefGoogle Scholar
Busse, F.H. 1978 Non-linear properties of thermal convection. Rep. Prog. Phys. 41 (12), 1929.CrossRefGoogle Scholar
Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard turbulence. Phys. fluids 17 (5), 055107.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chang, H.-C. & Wang, L.-C. 2010 A simple proof of Thue's theorem on circle packing. arXiv:1009.4322.Google Scholar
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent convection scaling exponent. Phys. Rev. Lett. 82 (20), 3998.CrossRefGoogle Scholar
Costa, P., Boersma, B.J., Westerweel, J. & Breugem, W.-P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.CrossRefGoogle ScholarPubMed
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2016 Universal scaling laws for dense particle suspensions in turbulent wall-bounded flows. Phys. Rev. Lett. 117 (13), 134501.CrossRefGoogle ScholarPubMed
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2018 Effects of the finite particle size in turbulent wall-bounded flows of dense suspensions. J. Fluid Mech. 843, 450–478.CrossRefGoogle Scholar
Demou, A.D. & Grigoriadis, D.G.E. 2019 Direct numerical simulations of Rayleigh–Bénard convection in water with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 881, 1073–1096.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Hirt, C.W. & Nichols, B.D. 1981 Volume of fluid (vof) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.CrossRefGoogle Scholar
Kang, C., Yoshikawa, H.N. & Mirbod, P. 2021 Onset of thermal convection in non-colloidal suspensions. J. Fluid Mech. 915, A128.CrossRefGoogle Scholar
Lakkaraju, R., Schmidt, L.E., Oresta, P., Toschi, F., Verzicco, R., Lohse, D. & Prosperetti, A. 2011 Effect of vapor bubbles on velocity fluctuations and dissipation rates in bubbly Rayleigh–Bénard convection. Phys. Rev. E 84 (3), 036312.CrossRefGoogle ScholarPubMed
Lakkaraju, R., Stevens, R.J.A.M., Oresta, P., Verzicco, R., Lohse, D. & Prosperetti, A. 2013 Heat transport in bubbling turbulent convection. Proc. Natl Acad. Sci. USA 110 (23), 9237–9242.CrossRefGoogle ScholarPubMed
Lashgari, I., Picano, F., Breugem, W.P. & Brandt, L. 2016 Channel flow of rigid sphere suspensions: particle dynamics in the inertial regime. Intl J. Multiphase Flow 78, 12–24.CrossRefGoogle Scholar
Liu, H.-R., Chong, K.L., Ng, C.S., Verzicco, R. & Lohse, D. 2021 a Enhancing heat transport in multiphase thermally driven turbulence. arXiv:2105.11327.Google Scholar
Liu, H.-R., Chong, K.L., Wang, Q., Ng, C.S., Verzicco, R. & Lohse, D. 2021 b Two-layer thermally driven turbulence: mechanisms for interface breakup. J. Fluid Mech. 913, R1.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Majlesara, M., Abouali, O., Kamali, R., Ardekani, M.N. & Brandt, L. 2020 Numerical study of hot and cold spheroidal particles in a viscous fluid. Intl J. Heat Mass Transfer 149, 119206.CrossRefGoogle Scholar
Metzger, B., Rahli, O. & Yin, X. 2013 Heat transfer across sheared suspensions: role of the shear-induced diffusion. J. Fluid Mech. 724, 527.CrossRefGoogle Scholar
Oberbeck, A. 1879 Über die wärmeleitung der flüssigkeiten bei berücksichtigung der strömungen infolge von temperaturdifferenzen. Ann. Phys. 243 (6), 271–292.CrossRefGoogle Scholar
Oresta, P. & Prosperetti, A. 2013 Effects of particle settling on Rayleigh–Bénard convection. Phys. Rev. E 87 (6), 063014.CrossRefGoogle ScholarPubMed
Oresta, P., Verzicco, R., Lohse, D. & Prosperetti, A. 2009 Heat transfer mechanisms in bubbly Rayleigh–Bénard convection. Phys. Rev. E 80 (2), 026304.CrossRefGoogle ScholarPubMed
Park, H.J., O'Keefe, K. & Richter, D.H. 2018 Rayleigh–Bénard turbulence modified by two-way coupled inertial, nonisothermal particles. Phys. Rev. Fluids 3 (3), 034307.CrossRefGoogle Scholar
Picano, F., Breugem, W.P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P., Mitra, D. & Brandt, L. 2013 Shear thickening in non-Brownian suspensions: an excluded volume effect. Phys. Rev. Lett. 111 (9), 098302.CrossRefGoogle Scholar
van der Poel, E.P., Stevens, R.J.A.M. & Lohse, D. 2013 Comparison between two-and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.CrossRefGoogle Scholar
Pouransari, H. & Mani, A. 2017 Effects of preferential concentration on heat transfer in particle-based solar receivers. J. Sol. Energy Engng 139 (2), 021008.CrossRefGoogle Scholar
du Puits, R., Resagk, C., Tilgner, A., Busse, F.H. & Thess, A. 2007 Structure of thermal boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 572, 231–254.CrossRefGoogle Scholar
Rahmani, M., Geraci, G., Iaccarino, G. & Mani, A. 2018 Effects of particle polydispersity on radiative heat transfer in particle-laden turbulent flows. Intl J. Multiphase Flow 104, 42–59.CrossRefGoogle Scholar
Roma, A.M., Peskin, C.S. & Berger, M.J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.CrossRefGoogle Scholar
Shishkina, O., Stevens, R.J.A.M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.CrossRefGoogle Scholar
Stevens, R.J.A.M., Clercx, H.J.H. & Lohse, D. 2010 Optimal Prandtl number for heat transfer in rotating Rayleigh–Bénard convection. New J. Phys. 12 (7), 075005.CrossRefGoogle Scholar
Ström, H. & Sasic, S. 2013 A multiphase DNS approach for handling solid particles motion with heat transfer. Intl J. Multiphase Flow 53, 75–87.CrossRefGoogle Scholar
Sugiyama, K., Ni, R., Stevens, R.J.A.M., Chan, T.S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105 (3), 034503.CrossRefGoogle ScholarPubMed
Tanaka, M. & Teramoto, D. 2015 Modulation of homogeneous shear turbulence laden with finite-size particles. J. Turbul. 16 (10), 979–1010.CrossRefGoogle Scholar
Thorpe, S.A. 2004 Recent developments in the study of ocean turbulence. Annu. Rev. Earth Planet. Sci. 32, 91–109.CrossRefGoogle Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47 (4), R2253.CrossRefGoogle ScholarPubMed
Uhlmann, M. 2005 An immersed boundary method with direct forcing for simulation of particulate flow. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Wang, J. & Xia, K.-Q. 2003 Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 32 (1), 127–136.CrossRefGoogle Scholar
Wang, Z., Mathai, V. & Sun, C. 2019 Self-sustained biphasic catalytic particle turbulence. Nat. Commun. 10 (1), 1–7.Google ScholarPubMed
Wesseling, P. 2009 Principles of Computational Fluid Dynamics, vol. 29. Springer.Google Scholar
Wyngaard, J.C. 1992 Atmospheric turbulence. Annu. Rev. Fluid Mech. 24 (1), 205–234.CrossRefGoogle Scholar
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75 (6), 066307.CrossRefGoogle ScholarPubMed
Xu, A., Tao, S., Shi, L. & Xi, H.-D. 2020 Transport and deposition of dilute microparticles in turbulent thermal convection. Phys. Fluids 32 (8), 083301.CrossRefGoogle Scholar
Yeo, K. & Maxey, M.R. 2010 Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J. Fluid Mech. 649, 205–231.CrossRefGoogle Scholar
Yeo, K. & Maxey, M.R. 2011 Numerical simulations of concentrated suspensions of monodisperse particles in a Poiseuille flow. J. Fluid Mech. 682, 491–518.CrossRefGoogle Scholar
Yousefi, A., Ardekani, M.N. & Brandt, L. 2020 Modulation of turbulence by finite-size particles in statistically steady-state homogeneous shear turbulence. J. Fluid Mech. 899, A19.CrossRefGoogle Scholar
Yousefi, A., Ardekani, M.N., Picano, F. & Brandt, L. 2021 Regimes of heat transfer in finite-size particle suspensions. Intl J. Heat Mass Transfer 177, 121514.CrossRefGoogle Scholar
Zade, S. 2019 Experimental studies of large particles in Newtonian and non-Newtonian fluids. PhD thesis, KTH Royal Institute of Technology.Google Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.CrossRefGoogle Scholar
Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76 (3), 036301.CrossRefGoogle Scholar