Published online by Cambridge University Press: 07 March 2012
Direct numerical simulation (DNS) is used to study the behaviour of stably-stratified turbulent channel flow with temperature-dependent fluid properties: specifically, viscosity (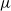 ) and thermal expansion coefficient (
) and thermal expansion coefficient (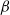 ). The governing equations are solved using a pseudo-spectral method for the case of turbulent water flow in a channel. A systematic campaign of simulations is performed in the shear Richardson number parameter space (
). The governing equations are solved using a pseudo-spectral method for the case of turbulent water flow in a channel. A systematic campaign of simulations is performed in the shear Richardson number parameter space (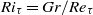 , where
, where 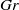 is the Grashof number and
is the Grashof number and 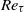 the shear Reynolds number), imposing constant-temperature boundary conditions. Variations of
the shear Reynolds number), imposing constant-temperature boundary conditions. Variations of 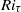 are obtained by changing
are obtained by changing 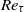 and keeping
and keeping 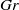 constant. Independently of the value of
constant. Independently of the value of 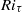 , all cases exhibit an initial transition from turbulent to laminar flow. A return transition to turbulence is observed only if
, all cases exhibit an initial transition from turbulent to laminar flow. A return transition to turbulence is observed only if 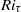 is below a threshold value (which depends also on the flow Reynolds number). After the transient evolution of the flow, a statistically-stationary condition occurs, in which active turbulence and internal gravity waves (IGW) coexist. In this condition, the transport efficiency of momentum and heat is reduced considerably compared to the condition of non-stratified turbulence. The crucial role of temperature-dependent viscosity and thermal expansion coefficient is directly demonstrated. The most striking feature produced by the temperature dependence of viscosity is flow relaminarization in the cold side of the channel (where viscosity is higher). The opposite behaviour, with flow relaminarization occurring in the hot side of the channel, is observed when a temperature-dependent thermal expansion coefficient is considered. We observe qualitative and quantitative modifications of structure and wall-normal position of internal waves compared to previous results obtained for uniform or quasi-uniform fluid properties. From the trend we observe in the investigated low-Reynolds-number range, we can hypothesize that, whereas the effects of temperature-dependent viscosity may be masked at higher Reynolds number, the effects of temperature-dependent thermal expansion coefficient will persist.
is below a threshold value (which depends also on the flow Reynolds number). After the transient evolution of the flow, a statistically-stationary condition occurs, in which active turbulence and internal gravity waves (IGW) coexist. In this condition, the transport efficiency of momentum and heat is reduced considerably compared to the condition of non-stratified turbulence. The crucial role of temperature-dependent viscosity and thermal expansion coefficient is directly demonstrated. The most striking feature produced by the temperature dependence of viscosity is flow relaminarization in the cold side of the channel (where viscosity is higher). The opposite behaviour, with flow relaminarization occurring in the hot side of the channel, is observed when a temperature-dependent thermal expansion coefficient is considered. We observe qualitative and quantitative modifications of structure and wall-normal position of internal waves compared to previous results obtained for uniform or quasi-uniform fluid properties. From the trend we observe in the investigated low-Reynolds-number range, we can hypothesize that, whereas the effects of temperature-dependent viscosity may be masked at higher Reynolds number, the effects of temperature-dependent thermal expansion coefficient will persist.
Present address: Department of Fluid Mechanics, CISM, 33100, Udine, Italy.