Article contents
Transition from hydrodynamic turbulence to magnetohydrodynamic turbulence in von Kármán flows
Published online by Cambridge University Press: 09 January 2012
Abstract
The influence of an externally applied magnetic field on flow turbulence is investigated in liquid-gallium von-Kármán (VK) swirling flows. Time-resolved measurements of global variables (such as the flow power consumption) and local recordings of the induced magnetic field are made. From these measurements, an effective Reynolds number is introduced as 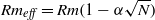 , so as to take into account the influence of the interaction parameter
, so as to take into account the influence of the interaction parameter 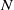 . This effective magnetic Reynolds number leads to unified scalings for both global variables and the locally induced magnetic field. In addition, when the flow rotation axis is perpendicular to the direction of the applied magnetic field, significant flow and induced magnetic field fluctuations are observed at low interaction parameter values, but corresponding to an Alfvèn speed
. This effective magnetic Reynolds number leads to unified scalings for both global variables and the locally induced magnetic field. In addition, when the flow rotation axis is perpendicular to the direction of the applied magnetic field, significant flow and induced magnetic field fluctuations are observed at low interaction parameter values, but corresponding to an Alfvèn speed 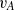 of the order of the fluid velocity fluctuations
of the order of the fluid velocity fluctuations 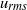 . This strong increase in the flow fluctuations is attributed to chaotic changes between hydrodynamic and magnetohydrodynamic velocity profiles.
. This strong increase in the flow fluctuations is attributed to chaotic changes between hydrodynamic and magnetohydrodynamic velocity profiles.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 4
- Cited by


