Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:31:51.274Z Has data issue: false hasContentIssue false
  • English
  • Français

Towards a finite-time singularity of the Navier–Stokes equations. Part 2. Vortex reconnection and singularity evasion

Published online by Cambridge University Press:  07 May 2019

H. K. Moffatt Open the ORCID record for H. K. Moffatt [Opens in a new window]  and
Yoshifumi Kimura
H. K. Moffatt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Yoshifumi Kimura
Affiliation:
Graduate School of Mathematics, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

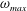In Part 1 of this work, we have derived a dynamical system describing the approach to a finite-time singularity of the Navier–Stokes equations. We now supplement this system with an equation describing the process of vortex reconnection at the apex of a pyramid, neglecting core deformation during the reconnection process. On this basis, we compute the maximum vorticity $\unicode[STIX]{x1D714}_{max}$ as a function of vortex Reynolds number 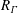$R_{\unicode[STIX]{x1D6E4}}$ in the range 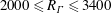$2000\leqslant R_{\unicode[STIX]{x1D6E4}}\leqslant 3400$, and deduce a compatible behaviour 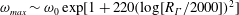$\unicode[STIX]{x1D714}_{max}\sim \unicode[STIX]{x1D714}_{0}\exp [1+220(\log [R_{\unicode[STIX]{x1D6E4}}/2000])^{2}]$ as 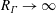$R_{\unicode[STIX]{x1D6E4}}\rightarrow \infty$. This may be described as a physical (although not strictly mathematical) singularity, for all 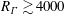$R_{\unicode[STIX]{x1D6E4}}\gtrsim 4000$.

JFM classification

Vortex Flows: Vortex dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , R1
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Hussain, F. & Duraisami, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23, 021701.Google Scholar
Jeong, J. T. & Moffatt, H. K. 1992 Free-surface cusps associated with flow at low Reynolds-number. J. Fluid Mech. 839, R2.Google Scholar
Kerr, R. M. 2018 Enstrophy and circulation scaling for Navier–Stokes reconnection. J. Fluid Mech. 241, 1–22.Google Scholar
McKeown, R., Ostilla-Monico, R., Pumir, A., Brenner, M. P. & Rubinstein, S. M. 2018 A cascade leading to the emergence of small structures in vortex ring collisions. Phys. Rev. Fluids 3, 124702.Google Scholar
Melander, M. V. & Hussain, F. 1989 Cross-linking of two antiparallel vortex tubes. Phys. Fluids A 1, 633–636.Google Scholar
Moffatt, H. K. & Kimura, Y. 2019 Towards a finite-time singularity of the Navier–Stokes equations. Part 1. J. Fluid Mech. 861, 950–967.Google Scholar