Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T12:41:38.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Stall onset on aerofoils at low to moderately high Reynolds number flows

Published online by Cambridge University Press:  24 September 2013

Wallace J. Morris II  and
Zvi Rusak
Wallace J. Morris II
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Zvi Rusak*
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The inception of leading-edge stall on stationary, two-dimensional, smooth, thin aerofoils at low to moderately high chord Reynolds number flows is investigated by a reduced-order, multiscale model problem via numerical simulations. The asymptotic theory demonstrates that a subsonic flow about a thin aerofoil can be described in terms of an outer region, around most of the aerofoil’s chord, and an inner region, around the nose, that asymptotically match each other. The flow in the outer region is dominated by the classical thin aerofoil theory. Scaled (magnified) coordinates and a modified (smaller) Reynolds number 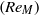$(R{e}_{M} )$ are used to correctly account for the nonlinear behaviour and extreme velocity changes in the inner region, where both the near-stagnation and high suction areas occur. It results in a model problem of a uniform, incompressible and viscous flow past a semi-infinite parabola with a far-field circulation governed by a parameter 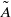$\tilde {A} $ that is related to the aerofoil’s angle of attack, nose radius of curvature, thickness ratio, and camber. The model flow problem is solved for various values of 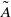$\tilde {A} $ through numerical simulations based on the unsteady Navier–Stokes equations. The value 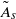${\tilde {A} }_{s} $ where a global separation zone first erupts in the nose flow, accompanied by loss of peak streamwise velocity ahead of it and change in shedding frequency behind it, is determined as a function of $R{e}_{M} $. These values indicate the stall onset on the aerofoil at various flow conditions. It is found that 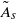${\tilde {A} }_{s} $ decreases with 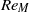$R{e}_{M} $ until some limit 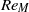$R{e}_{M} $ (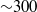${\sim }300$) and then increases with further increase of Reynolds number. At low values of 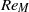$R{e}_{M} $ the flow is laminar and steady, even when stall occurs. The flow in this regime is dominated by the increasing effect of the adverse pressure gradient, which eventually overcomes the ability of the viscous stress to keep the boundary layer attached to the aerofoil. The change in the nature of stall at the limit 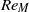$R{e}_{M} $ is attributed to the appearance of downstream travelling waves in the boundary layer that shed from the marginal separation zone and grow in size with either 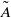$\tilde {A} $ or 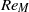$R{e}_{M} $. These unsteady, convective vortical structures relax the effect of the adverse pressure gradient on the viscous boundary layer to delay the onset of stall in the mean flow to higher values of 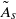${\tilde {A} }_{s} $. Computed results show agreement with marginal separation theory at low 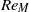$R{e}_{M} $ and with available experimental data at higher $R{e}_{M} $. This simplified approach provides a universal criterion to determine the stall angle of stationary thin aerofoils with a parabolic nose.

JFM classification

Aerodynamics: Aerodynamics Boundary Layers: Boundary Layers Boundary Layers: Boundary layer separation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 439 - 472
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, I. H. & von Doenhoff, A. E. 1958 Theory of Wing Sections, 2nd edn. Dover.Google Scholar
Anderson, J. D. Jr 2007 Fundamentals of Aerodynamics, 4th edn. McGraw-Hill.Google Scholar
Batchelor, G. K 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bhaskaran, R. & Rothmayer, A. P. 1998 Separation and instabilities in the viscous flow over airfoil leading edges. Comput. Fluids 27 (8), 903–921.CrossRefGoogle Scholar
Carr, L. W. 1988 Progress in analysis and prediction of dynamic stall. J. Aircraft 25 (1), 6–17.Google Scholar
Cebeci, T., Khattab, A. K. & Stewartson, K. 1980 On nose separation. J. Fluid Mech. 97, 435–454.CrossRefGoogle Scholar
Cheng, H. K. & Smith, F. T. 1982 The influence of airfoil thickness and Reynolds number on separation. J. Appl. Math. Phys. (Z. Angew. Math. Phys.) 33, 151–180.Google Scholar
van Dommelen, L. L. & Shen, S. F. 1980 The spontaneous generation of the singularity in a separating laminar boundary layer. J. Comput. Phys. 38 (2), 125–140.Google Scholar
Elliott, J. W. & Smith, F. T. 1987 Dynamic stall due to unsteady marginal separation. J. Fluid Mech. 179, 489–512.Google Scholar
Gault, D. E. 1957 A correlation of low-speed, airfoil-section stalling characteristics with Reynolds number and airfoil geometry. NACA TN 3963.Google Scholar
Grove, D. V., Laiosa, J. P., Woodson, S. H. & Stookesberry, D. C. 2002 Computational fluid dynamics study of an abrupt wing stall phenomena on the F/A-18E. AIAA Paper 2002-1025.Google Scholar
Hoffmann, K. A. & Chiang, S. T. 1993 Computational Fluid Dynamics for Engineers. Engineering Education System.Google Scholar
Jacobs, E. N. & Sherman, A. 1937 Airfoil section characteristics as affected by variations of the Reynolds number. NACA Report 586.Google Scholar
Jones, B. M. 1934 Stalling. J. R. Aero Soc. 38, 753–770.Google Scholar
Kunz, P. J. & Kroo, I. 2001 Analysis and design of airfoils for use at ultra-low Reynolds numbers. In Fixed and Flapping Wing Aerodynamics for Micro Air Vehicle Applications (ed. Muller, T. J.), Prog. in Astronautics and Aeronautics, vol. 195, AIAA.Google Scholar
Liebeck, R. H. 1973 A class of airfoils designed for high lift in incompressible flow. J. Aircraft 10 (10), 610–617.Google Scholar
McCormick, B. W. 1995 Aerodynamics, Aeronautics and Flight Mechanics, 2nd edn. Wiley.Google Scholar
Morris, W. J. II 2009 A universal prediction of stall onset for airfoils over a wide range of Reynolds number flows. PhD thesis, Rensselaer Polytechnic Institute, Troy, NY.Google Scholar
Nakayama, Y. 1988 Visualized Flow. Pergamon.Google Scholar
Pavelka, J. & Tatum, K. 1981 Validation of a wing leading-edge stall prediction technique. J. Aircraft 18 (10), 849–854.Google Scholar
Pinier, J. T., Ausseur, J. M., Glauser, M. N. & Higuchi, H. 2007 Proportional closed-loop feedback control of flow separation. AIAA J. 45 (1), 181–190.Google Scholar
Roache, P. J. 1998 Fundamentals of Computational Fluid Dynamics. Hermosa.Google Scholar
Ruban, A. I. 1982 Asymptotic theory of short separation bubbles at the leading edge of a thin airfoil. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza (1), 42–52.Google Scholar
Rusak, Z. 1994 Subsonic flow around the leading edge of a thin aerofoil with a parabolic nose. Eur. J. Appl. Maths 5, 283–311.CrossRefGoogle Scholar
Rusak, Z. & Morris, W. J. II 2011 Stall onset on airfoils at moderately high to high Reynolds number flows. Trans. ASME: J. Fluids Engng 133 (11), 111104.Google Scholar
Selig, M. S., Lyon, C. A., Giguere, P., Ninham, C. P. & Guglielmo, J. J. 1996 Summary of low-speed airfoil data, vol. 2. Department of Aero. & Astro. Engineering, University of Illinois at Urbana-Champaign.Google Scholar
Sousa, E. 2003 The controversial stability analysis. Appl. Maths Comput. 145 (2/3), 777–794.Google Scholar
Stewartson, K., Smith, F. T. & Kaups, K. 1982 Marginal separation. Stud. Appl. Maths 67 (1), 45–61.Google Scholar
Sychev, V. V., Ruban, A. I., Sychev, V. V. & Korolev, G. L. 1998 Asymptotic Theory of Separated Flows. Cambridge University Press.Google Scholar
Tani, I. 1964 Low speed flows involving bubble separations. Prog. Aerosp. Sci. 5, 70–103.Google Scholar
Thompson, H. D., Webb, B. W. & Hoffman, J. D. 1985 The cell Reynolds number myth. Intl J. Numer. Meth. Fluids 5, 305–310.CrossRefGoogle Scholar
Webster, B. E., Shephard, M. S., Rusak, Z. & Flaherty, J. E. 1994 Automated adaptive time-discontinuous finite-element method for unsteady compressible aerofoil aerodynamics. AIAA J. 32 (4), 748–757.Google Scholar
Werle, M. J. & Davis, R. T. 1972 Incompressible laminar boundary layers on a parabola at angle of attack: a study of the separation point. Trans. ASME: J. Appl. Mech. 39 (1), 7–12.CrossRefGoogle Scholar
Yen, S. C. & Huang, L.-C. 2009 Flow patterns and aerodynamic performance of unswept and swept-back wings. Trans. ASME: J. Fluids Engng 131 (11)111101.Google Scholar