Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T08:46:25.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectrum of passive scalars of high molecular diffusivity in turbulent mixing

Published online by Cambridge University Press:  28 January 2013

P. K. Yeung  and
K. R. Sreenivasan
P. K. Yeung*
Affiliation:
Schools of Aerospace Engineering, Computational Science and Engineering, and Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
K. R. Sreenivasan
Affiliation:
Department of Physics and Courant Institute of Mathematical Sciences, New York University, NY 10012, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the mixing of passive scalars transported in turbulent flow, with a molecular diffusivity that is large compared to the kinematic viscosity of the fluid. This particular case of mixing has not received much attention in experiment or simulation even though the first putative theory, due to Batchelor, Howells & Townsend (J. Fluid Mech., vol. 5, 1959, pp. 134–139), is now more than 50 years old. 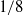We study the problem using direct numerical simulation of decaying scalar fields in steadily sustained homogeneous turbulence as the Schmidt number (the ratio of the kinematic viscosity of the fluid to the molecular diffusivity of the scalar) is allowed to vary from $1/ 8$ to 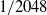$1/ 2048$ for two values of the microscale Reynolds number, 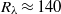${R}_{\lambda } \approx 140$ and 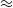$\approx $240. The simulations show that the passive scalar spectrum assumes a slope of 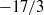$- 17/ 3$ in a range of scales, as predicted by the theory, when the Schmidt number is small and the Reynolds number is simultaneously large. The observed agreement between theory and simulation in the prefactor in the spectrum is not perfect. We assess the reasons for this discrepancy by a careful examination of the scalar evolution equation in the light of the assumptions of the theory, and conclude that the finite range of scales resolved in simulations is the main reason. Numerical issues specific to the regime of very low Schmidt numbers are also addressed briefly.

JFM classification

Mixing: Turbulent mixing Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , R14
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. 2. The case of large conductivity. J. Fluid Mech. 5, 134–139.CrossRefGoogle Scholar
Bogucki, D., Domaradzki, J. A. & Yeung, P. K. 1997 Direct numerical simulations of passive scalars with $Pr\gt 1$ advected by turbulent flow. J. Fluid Mech. 343, 111–130.CrossRefGoogle Scholar
Clay, J. P. 1973 Turbulent mixing of temperature in water, air and mercury. PhD thesis, University of California at San Diego.Google Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
Donzis, D. A. & Sreenivasan, K. R. 2010 The bottleneck effect and the Kolmogorov constant in isotropic turbulence. J. Fluid Mech. 657, 171–188.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2010 The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow Turbul. Combust. 85, 549–566.CrossRefGoogle Scholar
Donzis, D. A. & Yeung, P. K. 2010 Resolution effects and scaling in numerical simulations of passive scalar mixing in turbulence. Physica D 239, 1278–1287.CrossRefGoogle Scholar
Eswaran, V. & Pope, S. B. 1988 Direct numerical simulations of the turbulent mixing of a passive scalar. Phys. Fluids 31, 506–520.CrossRefGoogle Scholar
Gibson, C. H. 1968 Fine structure of scalar fields mixed by turbulence. II. Spectral theory. Phys. Fluids 11, 2316–2327.CrossRefGoogle Scholar
Gibson, C. H. & Schwarz, W. H. 1963 The universal equilibrium spectra of turbulent velocity and scalar fields. J. Fluid Mech. 16, 365–384.CrossRefGoogle Scholar
Gotoh, T. & Yeung, P. K. 2013 Passive scalar transport in turbulence: a computational perpsective. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.). Cambridge University Press.Google Scholar
Hill, R. J. 1978 Models of the scalar spectrum for turbulent dispersion. J. Fluid Mech. 88, 541–562.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Miller, P. L. & Dimotakis, P. E. 1996 Measurements of scalar power spectra in high Schmidt number turbulent jets. J. Fluid Mech. 308, 129–146.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Peclet-number grid turbulence. J. Fluid Mech. 358, 135–175.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.CrossRefGoogle Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8, 189–196.CrossRefGoogle Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17, 081703.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1993 Differential diffusion of passive scaalrs in isotropic turbulence. Phys. Fluids A 5, 2467–2478.CrossRefGoogle Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the Kolmogorov constant in numerical simulations of turbulence. Phys. Rev. E 56, 1746–1752.CrossRefGoogle Scholar