Published online by Cambridge University Press: 19 September 2014
Unlike the classical scaling relations for the mean-velocity profiles of wall-bounded uniform turbulent flows (the law of the wall, the defect law and the log law), which are predicated solely on dimensional analysis and similarity assumptions, scaling relations for the turbulent-energy spectra have been informed by specific models of wall turbulence, notably the attached-eddy hypothesis. In this paper, we use dimensional analysis and similarity assumptions to derive three scaling relations for the turbulent-energy spectra, namely the spectral analogues of the law of the wall, the defect law and the log law. By design, each spectral analogue applies in the same spatial domain as the attendant scaling relation for the mean-velocity profiles: the spectral analogue of the law of the wall in the inner layer, the spectral analogue of the defect law in the outer layer and the spectral analogue of the log law in the overlap layer. In addition, as we are able to show without invoking any model of wall turbulence, each spectral analogue applies in a specific spectral domain (the spectral analogue of the law of the wall in the high-wavenumber spectral domain, where viscosity is active, the spectral analogue of the defect law in the low-wavenumber spectral domain, where viscosity is negligible, and the spectral analogue of the log law in a transitional intermediate-wavenumber spectral domain, which may become sizable only at ultra-high 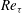 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau }$), with the implication that there exist model-independent one-to-one links between the spatial domains and the spectral domains. We test the spectral analogues using experimental and computational data on pipe flow and channel flow.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau }$), with the implication that there exist model-independent one-to-one links between the spatial domains and the spectral domains. We test the spectral analogues using experimental and computational data on pipe flow and channel flow.