Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T12:59:41.653Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulation of turbulent boundary layer wall pressure fluctuations via Poisson equation and synthetic turbulence

Published online by Cambridge University Press:  04 August 2017

Nan Hu Open the ORCID record for Nan Hu [Opens in a new window] ,
Nils Reiche  and
Roland Ewert
Nan Hu*
Affiliation:
Institute of Aerodynamics and Flow Technology, Department of Technical Acoustics, German Aerospace Center (DLR), Lilienthalplatz 7, 38108 Braunschweig, Germany
Nils Reiche
Affiliation:
Institute of Aerodynamics and Flow Technology, Department of Technical Acoustics, German Aerospace Center (DLR), Lilienthalplatz 7, 38108 Braunschweig, Germany
Roland Ewert
Affiliation:
Institute of Aerodynamics and Flow Technology, Department of Technical Acoustics, German Aerospace Center (DLR), Lilienthalplatz 7, 38108 Braunschweig, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

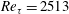Flat plate turbulent boundary layers under zero pressure gradient are simulated using synthetic turbulence generated by the fast random particle–mesh method. The stochastic realisation is based on time-averaged turbulence statistics derived from Reynolds-averaged Navier–Stokes simulation of flat plate turbulent boundary layers at Reynolds numbers $\mathit{Re}_{\unicode[STIX]{x1D70F}}=2513$ and 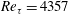$\mathit{Re}_{\unicode[STIX]{x1D70F}}=4357$. To determine fluctuating pressure, a Poisson equation is solved with an unsteady right-hand side source term derived from the synthetic turbulence realisation. The Poisson equation is solved via fast Fourier transform using Hockney’s method. Due to its efficiency, the applied procedure enables us to study, for high Reynolds number flow, the effect of variations of the modelled turbulence characteristics on the resulting wall pressure spectrum. The contributions to wall pressure fluctuations from the mean-shear turbulence interaction term and the turbulence–turbulence interaction term are studied separately. The results show that both contributions have the same order of magnitude. Simulated one-point spectra and two-point cross-correlations of wall pressure fluctuations are analysed in detail. Convective features of the fluctuating pressure field are well determined. Good agreement for the characteristics of the wall pressure fluctuations is found between the present results and databases from other investigators.

JFM classification

Acoustics: Aeroacoustics Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 421 - 454
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arguillat, B., Ricot, D., Robert, G. & Bailly, C.2005 Measurements of wavenumber–frequency spectrum of wall pressure fluctuations under turbulent flows. AIAA Paper 2005-2855.Google Scholar
Bailly, C. & Juvé, D.1999 A stochastic approach to compute subsonic noise using linearized Euler’s equations. AIAA Paper 1999-1872.CrossRefGoogle Scholar
Batchelor, G. K. 1982 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Blake, W. K. 1970 Turbulent boundary layer wall pressure fluctuations on smooth or rough walls. J. Fluid Mech. 44 (4), 637–660.CrossRefGoogle Scholar
Blake, W. K. 1986 Mechanics of Flow-Induced Sound and Vibration. Academic Press.Google Scholar
Bull, M. K. 1967 Wall pressure fluctuations associated with subsonic turbulent boundary layer flow. J. Fluid Mech. 28, 719–754.CrossRefGoogle Scholar
Chang, P., Piomelli, U. & Blake, W. K. 1999 Relationship between wall pressure and velocity-field sources. Phys. Fluids 11, 3434–3448.Google Scholar
Chase, D. M. 1980 Modeling the wave-vector frequency spectrum of turbulent boundary layer wall pressure. J. Sound Vib. 70, 29–68.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
Choi, H. & Moin, P. 1990 On the space–time characteristics of wall-pressure fluctuations. Phys. Fluids A 2 (8), 1450–1460.Google Scholar
Corcos, G. M. 1964 The structure of the turbulent pressure field in boundary layer flows. J. Fluid Mech. 18, 353–378.CrossRefGoogle Scholar
Crighton, D. G., Dowling, A. P., Williams, J. E. F., Heckl, M. & Leppington, F. G. 1992 Modern Methods in Analytical Acoustics. Springer.Google Scholar
Ehrenfried, K. & Koop, L.2008 Experimental study of pressure fluctuations beneath a compressible turbulent boundary layer. AIAA Paper 2008-2800.Google Scholar
Eitel-Amor, G., Örlü, R. & Schlatter, P. 2014 Simulation and validation of a spatially evolving turbulent boundary layer up to Re 𝜃 = 8300. Intl J. Heat Fluid Flow 47, 57–69.Google Scholar
Ewert, R. 2008 Broadband slat noise prediction based on CAA and stochasic sound sources from a fast random particle-mesh (rpm) method. Comput. Fluids 37, 369–387.Google Scholar
Ewert, R.2016 Canonical stochastic realization of turbulent sound sources via forced linear advection–diffusion–dissipation equation. AIAA Paper 2016-2965.Google Scholar
Ewert, R., Dierke, J., Siebert, J., Neifeld, A., Appel, C., Siefert, M. & Kornow, O. 2011 CAA broadband noise prediction for aeroacoustic design. J. Sound Vib. 330, 4139–4160.Google Scholar
Farabee, T. M. & Casarella, M. J. 1991 Spectral features of wall pressure fluctuations beneath turbulent boundary layers. Phys. Fluids A 3 (10), 2410–2420.Google Scholar
Gabriel, C., Müller, S., Ullrich, F. & Lerch, R. 2014 A new kind of sensor array for measuring spatial coherence of surface pressure on a car’s side window. J. Sound Vib. 333 (3), 901–915.Google Scholar
Gloerfelt, X. & Berland, J. 2013 Turbulent boundary layer wall pressure fluctuations on smooth or rough walls. J. Fluid Mech. 723, 318–351.Google Scholar
Goody, M. 2004 Empirical spectral model of surface pressure fluctuations. AIAA J. 42 (9), 1788–1794.Google Scholar
Herr, M.2013 Trailing-edge noise – reduction concepts and scaling laws. PhD thesis, Institute of Aerodynamics and Flow Technology, German Aerospace Center.Google Scholar
Hockney, R. W. & Eastwood, J. W. 1988 Computer Simulation Using Particles. Taylor & Francis.Google Scholar
Hodgson, T. H.1962 Pressure fluctuations in shear flow turbulence. PhD thesis, University of London.Google Scholar
Howe, M. 1998 Acoustics of Fluid–Structure Interactions. Cambridge University Press.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.Google Scholar
Hu, N. & Herr, M.2016 Characteristics of wall pressure fluctuations for a flat plate turbulent boundary layer with pressure gradients. AIAA Paper 2016-2749.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Johansson, A. V., Her, J. Y. & Haritonidis, J. H. 1987 On the generation of high-amplitude wall-pressure peaks in turbulent boundary layers and spots. J. Fluid Mech. 175, 119–142.Google Scholar
Kamruzzaman, M., Lutz, T., Herrig, A. & Krämer, E. 2012 Semi-empirical modeling of turbulent anisotropy for airfoil self-noise predictions. AIAA J. 50 (1), 46–60.CrossRefGoogle Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kraichnan, R. H. 1956 Pressure fluctuations in turbulent flow over a flat plate. J. Acoust. Soc. Am. 28 (3), 378–390.Google Scholar
Leclercq, D. J. J. & Bohineust, X. 2002 Modeling the wave-vector frequency spectrum of turbulent boundary layer wall pressure. J. Sound Vib. 257 (3), 477–501.Google Scholar
Meecham, W. C. & Tavis, M. T. 1980 Theoretical pressure correlation functions in turbulent boundary layer. Phys. Fluids 23, 1119–1131.Google Scholar
Palumbo, D. 2012 Determining correlation and coherence lengths in turbulent boundary layer flight data. J. Sound Vib. 331, 3721–3737.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Schlatter, P., Örlü, R., Li, Q., Fransson, J., Johansson, A., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to Re 𝜃 through simulation and experiments. Phys. Fluids 21, 05702.Google Scholar
Siefert, M. & Ewert, R.2009 Sweeping sound generation in jets realized with a random particle-mesh method. AIAA Paper 2009-3369.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to Re 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Tam, C. K. W. & Auriault, L. 1999 Jet mixing noise from fine-scale turbulence. AIAA J. 37 (2), 145–153.Google Scholar
Viazzo, S., Dejoan, A. & Schiestel, R. 2001 Spectral features of the wall-pressure fluctuations in turbulent wall flows with and without perturbations using LES. J. Heat Fluid Flow 22, 39–52.Google Scholar
Wilcox, D. C. 2006 Turbulence Modeling for CFD, 3rd edn. DCW Industries.Google Scholar
Willmarth, W. W. & Wooldridge, C. E. 1962 Measurements of the fluctuating pressure at the wall beneath a thick turbulent boundary layer. J. Fluid Mech. 14, 187–210.Google Scholar
Wooldridge, C. E. & Willmarth, W. W.1962 Measurements of the correlation between the fluctuating velocities and the fluctuating wall pressure in a thick turbulent boundary layer. Tech. Rep. The University of Michigan, Department of Aeronautical and Astronautical Engineering.Google Scholar