Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T00:47:12.138Z Has data issue: false hasContentIssue false
  • English
  • Français

Ship generated mini-tsunamis

Published online by Cambridge University Press:  03 March 2017

John Grue Open the ORCID record for John Grue [Opens in a new window]
John Grue*
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, Oslo, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

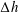Very long waves are generated when a ship moves across an appreciable depth change $\unicode[STIX]{x0394}h$ comparable to the average and relatively shallow water depth 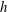$h$ at the location, with 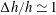$\unicode[STIX]{x0394}h/h\simeq 1$. The phenomenon is new and the waves were recently observed in the Oslofjord in Norway. The 0.5–1 km long waves, extending across the 2–3 km wide fjord, are observed as run-ups and run-downs along the shore, with periods of 30–60 s, where a wave height up to 1.4 m has been measured. The waves travelling with the shallow water speed, found ahead of the ships moving at subcritical depth Froude number, behave like a mini-tsunami. A qualitative explanation of the linear generation mechanism is provided by an asymptotic analysis, valid for $\unicode[STIX]{x0394}h/h\ll 1$ and long waves, expressing the generation in terms of a pressure impulse at the depth change. Complementary fully dispersive calculations for 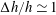$\unicode[STIX]{x0394}h/h\simeq 1$ document symmetries of the waves at positive or negative 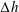$\unicode[STIX]{x0394}h$. 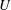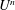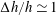The wave height grows with the ship speed $U$ according to $U^{n}$ with $n$ in the range 3–4, for $\unicode[STIX]{x0394}h/h\simeq 1$, while the growth in 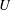$U$ is only very weak for 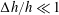$\unicode[STIX]{x0394}h/h\ll 1$ (the asymptotics). Calculations show good agreement with observations.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Topographic effects Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 142 - 166
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, E. D., Bucksbaum, S. B., Hall, R. E., Penhune, J. P., Schmitt, K. F., Watson, K. M. & Wyatt, D. C. 1989 Observation of a nonlinear solitary wave packet in the Kelvin wake of a ship. J. Fluid Mech. 204, 263–293.Google Scholar
Clamond, D. & Grue, J. 2001 A fast method for fully nonlinear water wave computations. J. Fluid Mech. 447, 337–355.Google Scholar
Clarisse, J.-M., Newman, J. N. & Ursell, F. 1995 Integrals with a large parameter: water waves on finite depth due to an impulse. Proc. R. Soc. Lond. A 450, 67–87.Google Scholar
Cole, S. L. 1985 Transient waves produced by flow past a bump. Wave Motion 7, 579–587.Google Scholar
Constantine, T. 1960 On the movement of ships in restricted waterways. J. Fluid Mech. 9, 247–256.Google Scholar
Didenkulova, I., Pelinovsky, E. & Soomere, T. 2011 Can the waves generated by fast ferries be a physical model of tsunami? Pure Appl. Geophys. 168, 2071–2082.Google Scholar
Ertekin, R. C., Webster, W. C. & Wehausen, J. V. 1986 Waves caused by a moving disturbance in a shallow channel of finite width. J. Fluid Mech. 169, 275–292.CrossRefGoogle Scholar
Fructus, D. & Grue, J. 2007 An explicit method for the nonlinear interaction between water waves and variable and moving bottom topography. J. Comput. Phys. 222, 720–739.Google Scholar
Glimsdal, S., Pedersen, G. K., Atakan, K., Harbitz, C. B., Langtangen, H. P. & Lovholt, F. 2006 Propagation of the Dec. 26, 2004, Indian ocean tsunami. Effects of dispersion and source characteristics. Intl J. Fluid Mech. Res. 33, 15–43.Google Scholar
Grue, J. 2002 On four highly nonlinear phenomena in wave theory and marine hydrodynamics. Appl. Ocean Res. 24, 261–274.Google Scholar
Grue, J. 2015 Nonlinear interfacial wave formation in three dimensions. J. Fluid Mech. 767, 735–762.Google Scholar
Hamer, M. 1999 Solitary killers. New Sci. 163 (2291), 18–19.Google Scholar
Harbitz, C. B. 1992 Model simulations of tsunamis generated by the Storegga slides. Mar. Geol. 105, 1–21.Google Scholar
Mei, C. C. 1989 The Applied Dynamics of Ocean Surface Waves. World Scientific.Google Scholar
Newman, J. N. 1977 Marine Hydrodynamics. MIT Press.Google Scholar
Pedersen, G. 1988 Three-dimensional wave patterns generated by moving disturbances at transcritical speeds. J. Fluid Mech. 196, 39–63.CrossRefGoogle Scholar
Pelinovksy, E. 2006 Hydrodynamics of tsunami waves. In Waves in Geophysical Fluids (ed. Grue, J. & Trulsen, K.), CISM Courses and Lectures No. 489, pp. 1–48. Springer.Google Scholar
Sibul, O. J., Webster, W. C. & Wehausen, J. V. 1979 A phenomenon observed in transient testing. Schiffstechnik 26, 179–200.Google Scholar
Soomere, T. 2005 Fast ferry traffic as a qualitatively new forcing factor of environmental processes in non-tidal sea areas: a case study in Tallinn Bay, Baltic sea. Environ. Fluid Mech. 5, 293–323.Google Scholar
Soomere, T. 2009 Long ship waves in shallow water bodies. In Applied Waves Mathematics (ed. Quak, E. & Soomere, T.), pp. 193–228. Springer.CrossRefGoogle Scholar
Torsvik, T. 2009 Modelling of ship waves from high-speed vessels. In Applied Waves Mathematics (ed. Quak, E. & Soomere, T.), pp. 229–263. Springer.Google Scholar
Torsvik, T., Pedersen, G. & Dysthe, K. 2009 Waves generated by a pressure disturbance moving in a channel with a variable cross-sectional topography. ASCE J. Waterway Port Coastal Ocean Engng 135 (5), 120–123.Google Scholar
Wu, J. & Chen, B. 2003 Unsteady ship waves in shallow water of varying depth based on Green-Naghdi equation. Ocean Engng 30, 1899–1913.Google Scholar
Wu, T. Y. 1987 Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 184, 75–99.CrossRefGoogle Scholar