Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhou, Ye
Groom, Michael
and
Thornber, Ben
2020.
Dependence of Enstrophy Transport and Mixed Mass on Dimensionality and Initial Conditions in the Richtmyer–Meshkov Instability Induced Flows1.
Journal of Fluids Engineering,
Vol. 142,
Issue. 12,
Sun, Rui
Ding, Juchun
Zhai, Zhigang
Si, Ting
and
Luo, Xisheng
2020.
Convergent Richtmyer–Meshkov instability of heavy gas layer with perturbed inner surface.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Zhou, Zhangbo
Ding, Juchun
Zhai, Zhigang
Cheng, Wan
and
Luo, Xisheng
2020.
Mode coupling in converging Richtmyer–Meshkov instability of dual-mode interface.
Acta Mechanica Sinica,
Vol. 36,
Issue. 2,
p.
356.
Al-Marouf, M.
and
Samtaney, R.
2020.
Effects of solid circular cylinders on the dynamics of the Richtmyer–Meshkov instability.
Shock Waves,
Vol. 30,
Issue. 4,
p.
409.
Li, Xinliang
Fu, Yaowei
Yu, Changping
and
Li, Li
2021.
Statistical characteristics of turbulent mixing in spherical and cylindrical converging Richtmyer–Meshkov instabilities.
Journal of Fluid Mechanics,
Vol. 928,
Issue. ,
Tang, Jinggang
Zhang, Fu
Luo, Xisheng
and
Zhai, Zhigang
2021.
Effect of Atwood number on convergent Richtmyer–Meshkov instability.
Acta Mechanica Sinica,
Vol. 37,
Issue. 3,
p.
434.
Dai, Jian
Xu, Fei
Cai, Xiaodong
and
Mahmoudi, Yasser
2021.
Effects of velocity shear layer on detonation propagation in a supersonic expanding combustor.
Physics of Fluids,
Vol. 33,
Issue. 10,
Chen, Feng
Xu, Aiguo
Zhang, Yudong
Gan, Yanbiao
Liu, Bingbing
and
Wang, Shuang
2022.
Effects of the initial perturbations on the Rayleigh—Taylor—Kelvin—Helmholtz instability system.
Frontiers of Physics,
Vol. 17,
Issue. 3,
Li, Jianming
Ding, Juchun
Luo, Xisheng
and
Zou, Liyong
2022.
Instability of a heavy gas layer induced by a cylindrical convergent shock.
Physics of Fluids,
Vol. 34,
Issue. 4,
Chen, Jie
Xu, Aiguo
Chen, Dawei
Zhang, Yudong
and
Chen, Zhihua
2022.
Discrete Boltzmann modeling of Rayleigh-Taylor instability: Effects of interfacial tension, viscosity, and heat conductivity.
Physical Review E,
Vol. 106,
Issue. 1,
Li, Linfei
Jin, Tai
Zou, Liyong
Luo, Kun
and
Fan, Jianren
2023.
Numerical study of Richtmyer–Meshkov instability of a flat interface driven by perturbed and reflected shock waves.
Physics of Fluids,
Vol. 35,
Issue. 2,
Zhang, Dejia
Xu, Aiguo
Song, Jiahui
Gan, Yanbiao
Zhang, Yudong
and
Li, Yingjun
2023.
Specific-heat ratio effects on the interaction between shock wave and heavy-cylindrical bubble: Based on discrete Boltzmann method.
Computers & Fluids,
Vol. 265,
Issue. ,
p.
106021.
Zhang, Yumeng
Zhao, Yong
Ding, Juchun
and
Luo, Xisheng
2023.
Richtmyer–Meshkov instability with a rippled reshock.
Journal of Fluid Mechanics,
Vol. 968,
Issue. ,
Dai, Jian
and
Liu, Jindian
2023.
Numerical study of detonation propagation under the action of supersonic pulsating flow in expanding combustor.
Acta Astronautica,
Vol. 211,
Issue. ,
p.
25.
Ren, Jinlian
Culp, David
Smith, Brandon
and
Ma, Xia
2023.
An investigation of the multi-mode Richtmyer-Meshkov instability at a gas/HE interface using Pagosa.
Computers & Mathematics with Applications,
Vol. 139,
Issue. ,
p.
136.
Zhang, Duo
Ding, Juchun
Li, Ming
Zou, Liyong
and
Luo, Xisheng
2023.
Effects of reverberating waves and interface coupling on a divergent Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Yuan, Ming
Zhao, Zhiye
Liu, Luoqin
Wang, Pei
Liu, Nan-Sheng
and
Lu, Xi-Yun
2023.
Instability evolution of a shock-accelerated thin heavy fluid layer in cylindrical geometry.
Journal of Fluid Mechanics,
Vol. 969,
Issue. ,
He, Yifeng
Peng, Naifu
Li, Haifeng
Tian, Baolin
and
Yang, Yue
2023.
Formation of the cavity on a planar interface subjected to a perturbed shock wave.
Physical Review Fluids,
Vol. 8,
Issue. 6,
Shan, Yiming
Xu, Aiguo
Wang, Lifeng
and
Zhang, Yudong
2023.
Nonequilibrium kinetics effects in Richtmyer–Meshkov instability and reshock processes.
Communications in Theoretical Physics,
Vol. 75,
Issue. 11,
p.
115601.
Liang, Yu
and
Luo, Xisheng
2023.
Hydrodynamic instabilities of two successive slow/fast interfaces induced by a weak shock.
Journal of Fluid Mechanics,
Vol. 955,
Issue. ,
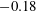 $-0.18$ to 0.67. Results indicate that the diffracted convergent shock increases its strength gradually and reduces its amplitude quickly when it propagates towards the convergence centre. After the strike of the diffracted convergent shock, the initially unperturbed interface deforms with a bulge structure at the centre and two interface steps at both sides, which can be ascribed to the non-uniformity of the pressure distribution behind the diffracted convergent shock. With the decrease of Atwood number, the bulge structure becomes more pronounced. Quantitatively, the interface amplitude experiences a fast but short growing stage and then enters a linear stage. A good collapse of the dimensionless amplitude is found for all cases, which indicates a weak dependence of the growth rate on Atwood number in the deformed shock-induced RM instability. Then the impulsive theory is modified by eliminating the Atwood number and considering the geometry convergence, which well predicts the amplitude growth for the deformed shock-induced RM instability. Finally, the underlying mechanism is decoupled into three parts, and it is found that both the impulsive pressure perturbation and the geometry convergence promote the growth of interface perturbation while the continuous pressure perturbation inhibits the growth. As the Atwood number decreases, the impulsive perturbation plays an increasingly important role, which suggests that the impulsive perturbation dominates the deformed shock-induced RM instability at the linear stage.
$-0.18$ to 0.67. Results indicate that the diffracted convergent shock increases its strength gradually and reduces its amplitude quickly when it propagates towards the convergence centre. After the strike of the diffracted convergent shock, the initially unperturbed interface deforms with a bulge structure at the centre and two interface steps at both sides, which can be ascribed to the non-uniformity of the pressure distribution behind the diffracted convergent shock. With the decrease of Atwood number, the bulge structure becomes more pronounced. Quantitatively, the interface amplitude experiences a fast but short growing stage and then enters a linear stage. A good collapse of the dimensionless amplitude is found for all cases, which indicates a weak dependence of the growth rate on Atwood number in the deformed shock-induced RM instability. Then the impulsive theory is modified by eliminating the Atwood number and considering the geometry convergence, which well predicts the amplitude growth for the deformed shock-induced RM instability. Finally, the underlying mechanism is decoupled into three parts, and it is found that both the impulsive pressure perturbation and the geometry convergence promote the growth of interface perturbation while the continuous pressure perturbation inhibits the growth. As the Atwood number decreases, the impulsive perturbation plays an increasingly important role, which suggests that the impulsive perturbation dominates the deformed shock-induced RM instability at the linear stage.


