Article contents
Re-entrant history force transition for stick–slip Janus swimmers: mixed Basset and slip-induced memory effects
Published online by Cambridge University Press: 06 November 2019
Abstract
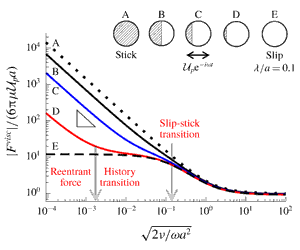
It is well known that a rigid non-slippery particle in unsteady motion can experience a Basset history force with the signature  $1/\unicode[STIX]{x1D6FF}$ decay due to a Stokes boundary layer of thickness
$1/\unicode[STIX]{x1D6FF}$ decay due to a Stokes boundary layer of thickness  $\unicode[STIX]{x1D6FF}$. For a uniform slip particle with slip length
$\unicode[STIX]{x1D6FF}$. For a uniform slip particle with slip length  $\unicode[STIX]{x1D706}$, however, a persistent force plateau can replace the usual Basset decay at
$\unicode[STIX]{x1D706}$, however, a persistent force plateau can replace the usual Basset decay at  $\unicode[STIX]{x1D6FF}$ below the slip–stick transition (SST) point
$\unicode[STIX]{x1D6FF}$ below the slip–stick transition (SST) point  $\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D706}$ (Premlata & Wei, J. Fluid Mech., vol. 866, 2019, pp. 431–449). Here we analyse the hydrodynamic force on an oscillating stick–slip Janus particle, showing that it can display unusual history force responses that are of neither the no-slip nor the purely slip type but mixed with both. Solving the oscillatory Stokes flow equation together with a matched asymptotic boundary layer theory, we find that the persistent force plateau seen for a uniform slip particle may be destroyed by the presence of the stick portion of a stick–slip Janus particle. Instead, a
$\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D706}$ (Premlata & Wei, J. Fluid Mech., vol. 866, 2019, pp. 431–449). Here we analyse the hydrodynamic force on an oscillating stick–slip Janus particle, showing that it can display unusual history force responses that are of neither the no-slip nor the purely slip type but mixed with both. Solving the oscillatory Stokes flow equation together with a matched asymptotic boundary layer theory, we find that the persistent force plateau seen for a uniform slip particle may be destroyed by the presence of the stick portion of a stick–slip Janus particle. Instead, a  $1/\unicode[STIX]{x1D6FF}$ Basset force of amplitude smaller than the no-slip counterpart will re-emerge to dominate the high frequency viscous force response again. This re-entry Basset force, which occurs only after making a stick patch on a slippery particle, is also found to depend solely on the coverage of the stick face irrespective of the slip length of the slip face. When the stick portion is small, in particular, the re-entry Basset decay will exhibit a slip plateau on its tail, displaying a distinctive re-entrant history force transition prior to the SST. But if changing this tiny stick face to be slippery, no matter how small the slip length is, the re-entry Basset decay will disappear and a constant force plateau will return to dominate the force response again. These unusual force responses arising from mixed stick–slip or non-uniform slip effects may not only provide unique hydrodynamic fingerprints for characterizing heterogeneous particles, but also have potential uses in active manipulation and sorting of these particles.
$1/\unicode[STIX]{x1D6FF}$ Basset force of amplitude smaller than the no-slip counterpart will re-emerge to dominate the high frequency viscous force response again. This re-entry Basset force, which occurs only after making a stick patch on a slippery particle, is also found to depend solely on the coverage of the stick face irrespective of the slip length of the slip face. When the stick portion is small, in particular, the re-entry Basset decay will exhibit a slip plateau on its tail, displaying a distinctive re-entrant history force transition prior to the SST. But if changing this tiny stick face to be slippery, no matter how small the slip length is, the re-entry Basset decay will disappear and a constant force plateau will return to dominate the force response again. These unusual force responses arising from mixed stick–slip or non-uniform slip effects may not only provide unique hydrodynamic fingerprints for characterizing heterogeneous particles, but also have potential uses in active manipulation and sorting of these particles.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 5
- Cited by


