Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T19:43:38.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Rarefaction-driven Rayleigh–Taylor instability. Part 2. Experiments and simulations in the nonlinear regime

Published online by Cambridge University Press:  12 January 2018

R. V. Morgan Open the ORCID record for R. V. Morgan [Opens in a new window] ,
W. H. Cabot ,
J. A. Greenough  and
J. W. Jacobs
R. V. Morgan*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
W. H. Cabot
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
J. A. Greenough
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
J. W. Jacobs
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experiments and large eddy simulation (LES) were performed to study the development of the Rayleigh–Taylor instability into the saturated, nonlinear regime, produced between two gases accelerated by a rarefaction wave. Single-mode two-dimensional, and single-mode three-dimensional initial perturbations were introduced on the diffuse interface between the two gases prior to acceleration. The rarefaction wave imparts a non-constant acceleration, and a time decreasing Atwood number, 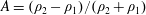$A=(\unicode[STIX]{x1D70C}_{2}-\unicode[STIX]{x1D70C}_{1})/(\unicode[STIX]{x1D70C}_{2}+\unicode[STIX]{x1D70C}_{1})$, where 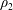$\unicode[STIX]{x1D70C}_{2}$ and $\unicode[STIX]{x1D70C}_{1}$ are the densities of the heavy and light gas, respectively. Experiments and simulations are presented for initial Atwood numbers of 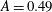$A=0.49$, 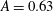$A=0.63$, 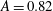$A=0.82$ and $A=0.94$. Nominally two-dimensional (2-D) experiments (initiated with nearly 2-D perturbations) and 2-D simulations are observed to approach an intermediate-time velocity plateau that is in disagreement with the late-time velocity obtained from the incompressible model of Goncharov (Phys. Rev. Lett., vol. 88, 2002, 134502). Reacceleration from an intermediate velocity is observed for 2-D bubbles in large wavenumber, 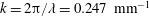$k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}=0.247~\text{mm}^{-1}$, experiments and simulations, where 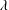$\unicode[STIX]{x1D706}$ is the wavelength of the initial perturbation. At moderate Atwood numbers, the bubble and spike velocities approach larger values than those predicted by Goncharov’s model. These late-time velocity trends are predicted well by numerical simulations using the LLNL Miranda code, and by the 2009 model of Mikaelian (Phys. Fluids., vol. 21, 2009, 024103) that extends Layzer type models to variable acceleration and density. Large Atwood number experiments show a delayed roll up, and exhibit a free-fall like behaviour. Finally, experiments initiated with three-dimensional perturbations tend to agree better with models and a simulation using the LLNL Ares code initiated with an axisymmetric rather than Cartesian symmetry.

JFM classification

Compressible Flows: Gas dynamics Instability: Nonlinear instability Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 320 - 355
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, M. J. & Dalziel, S. B. 2010 Small Atwood number Rayleigh–Taylor experiments. Phil. Trans. R. Soc. Lond. A 368 (1916), 1663–1679.Google Scholar
Baker, G. R., Meiron, D. I. & Orszag, S. A. 1980 Vortex simulation of the Rayleigh–Taylor instability. Phys. Fluids 23 (8), 1485–1490.Google Scholar
Banerjee, A. & Andrews, M. J. 2006 Statistically steady measurements of Rayleigh–Taylor mixing in a gas channel. Phys. Fluids 18 (3), 035107.Google Scholar
Betti, R. & Sanz, J. 2006 Bubble acceleration in the ablative Rayleigh–Taylor instability. Phys. Rev. Lett. 97, 205002.Google Scholar
Cabot, W. H. 2006 Comparison of two- and three-dimensional simulations of miscible Rayleigh–Taylor instability. Phys. Fluids 18, 045101.Google Scholar
Clavin, P. & Williams, F. 2005 Asymptotic spike evolution in Rayleigh–Taylor instability. J. Fluid Mech. 525, 105–113.Google Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF6 interface. J. Fluid Mech. 464, 113–136.Google Scholar
Cook, A. W. 2007 Artificial fluid properties for large-eddy simulation of compressible turbulent mixing. Phys. Fluids 19, 055103.Google Scholar
Cook, A. W. 2009 Enthaply diffusion in multicomponent flows. Phys. Fluids 21, 055109.CrossRefGoogle Scholar
Cook, A. W. & Cabot, W. H. 2004 A high-wavenumber viscosity for high-resolution numerical methods. J. Comput. Phys. 195, 594–601.CrossRefGoogle Scholar
Cook, A. W. & Cabot, W. H. 2005 Hyperviscosity for shock-turbulence interactions. J. Comp. Phys. 203, 379–385.CrossRefGoogle Scholar
Cook, A. W. & Dimotakis, P. E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.CrossRefGoogle Scholar
Davies, R. M. & Taylor, G. 1950 The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Proc. R. Soc. Lond. A 200, 375–390.Google Scholar
Dimonte, G. 1999 Nonlinear evolution of the Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Plasmas 6 (5), 2009–2015.CrossRefGoogle Scholar
Dimonte, G., Gore, R. & Schneider, M. 1998 Rayleigh–Taylor instability in elastic-plastic materials. Phys. Rev. Lett. 80 (6), 1212–1215.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulence. J. Fluid Mech. 409, 69–97.Google Scholar
Glimm, J. & Li, X. L. 1988 Validation of the Sharp-Wheeler bubble merger model from experimental and computational data. Phys. Fluids 31 (8), 2077–2085.Google Scholar
Goncharov, V. N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88 (13), 134502.Google Scholar
Jacobs, J. W. & Catton, I. 1988 Three-dimensional Rayleigh–Taylor instability. Part 2. Experiment. J. Fluid Mech. 187, 353–371.CrossRefGoogle Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.Google Scholar
Jacobs, J. W., Krivets, V. V., Tsiklashvili, V. & Likhachev, O. A. 2013 Experiments on the Richtmyer–Meshkov instability with an imposed, random initial perturbation. Shock Waves 23 (4), 407–413.Google Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9, 3078–3085.Google Scholar
Kolev, Tz. V. & Rieben, R. N. 2009 A tensor artificial viscosity using finite element approach. J. Comp. Phys. 228, 8336–8366.CrossRefGoogle Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. Rev. J. 122, 1–12.CrossRefGoogle Scholar
Lewis, D. J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes 2. Proc. R. Soc. Lond. A 202 (1068), 81–96.Google Scholar
Long, C. C., Krivets, V. V., Greenough, J. A. & Jacobs, J. W. 2009 Shock tube experiments and numerical simulation of the single-mode, three-dimensional Richtmyer–Meshkov instability. Phys. Fluids 21, 114104.CrossRefGoogle Scholar
McFarland, J. A., Greenough, J. A. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84, 026303.Google ScholarPubMed
Menikoff, R. & Zemach, C. 1983 Rayleigh–Taylor instability and the use of conformal maps for ideal fluid flow. J. Comput. Phys. 51, 28–64.Google Scholar
Mikaelian, K. O. 2008 Limitations and failures of the Layzer model for hydrodynamic instabilities. Phys. Rev. E 78, 015303.Google Scholar
Mikaelian, K. O. 2009 Reshocks, rarefactions, and the generalized Layzer model for hydrodynamic instabilities. Phys. Fluids 21 (2), 024103.Google Scholar
Mikaelian, K. O. 2014 Solution to Rayleigh–Taylor instabilities: bubbles, spikes, and their scalings. Phys. Rev. E 89, 053009.Google Scholar
Morgan, R. V., Likhachev, O. A. & Jacobs, J. W. 2016 Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory. J. Fluid Mech 791, 34–60.Google Scholar
Oron, D., Arazi, L., Kartoon, D., Rikanati, A., Alon, U. & Shvarts, D. 2001 Dimensionality dependence of the Rayleigh–Taylor and Richtmyer–Meshkov instability late-time scaling laws. Phys. Plasmas 8, 2108–2115.Google Scholar
Owczarek, J. A. 1964 Fundamentals of Gas Dynamics. International Textbook Co.Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101, 104–129.Google Scholar
Popil, R. & Curzon, F. L. 1979 Production of reproducible Rayleigh–Taylor instabilities. Rev. Sci. Instrum. 50 (10), 1291–1295.Google Scholar
Ramaprabhu, P. & Dimonte, G. 2005 Single-mode dynamics of the Rayleigh–Taylor instability at any density ratio. Phys. Rev. E 71 (3), 036314.Google Scholar
Ramaprabhu, P., Dimonte, G., Woodward, P., Fryer, C., Rockefeller, G., Muthuraman, K., Lin, P.-H. & Jayaraj, J. 2012 The late-time dynamics of the single-mode Rayleigh–Taylor instability. Phys. Fluids 24 (7), 074107.Google Scholar
Ramaprabhu, P., Dimonte, G., Young, Y.-N., Calder, A. C. & Fryxell, B. 2006 Limits of the potential flow approach to the single-mode Rayleigh–Taylor problem. Phys. Rev. E 74 (6), 066308.Google Scholar
Ratafia, M. 1973 Experimental investigation of Rayleigh–Taylor instability. Phys. Fluids 16 (8), 1207–1210.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Reckinger, S. J., Livescu, D. & Vasilyev, O. V. 2010 Adaptive wavelet collocation method simulation of Rayleigh–Taylor instability. Phys. Scr. T142, 014064.CrossRefGoogle Scholar
Reckinger, S. J., Livescu, D. & Vasilyev, O. V. 2016 Comprehensive numerical methodology for direct numerical simulations of compressible Rayleigh–Taylor instability. J. Comput. Phys. 313, 181–208.Google Scholar
Settles, G. S. 2001 Schlieren and Shadowgraph Techniques. Springer.Google Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12 (1–3), 3–18.CrossRefGoogle Scholar
Sharp, R. W. Jr. & Barton, R. T. 1981 Hemp advection model. UCID-17809 Rev.1, Lawrence Livermore Laboratory.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes 1. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Thompson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68, 1–24.Google Scholar
Wei, T. & Livescu, D. 2012 Late-time quadratic growth in single-mode Rayleigh–Taylor instability. Phys. Rev. E 86 (4), 046405.Google Scholar
Wilkins, M. L.1963 Calculation of elastic-plastic flow. UCRL-7322, Lawrence Radiation Laboratory.Google Scholar
Wilkinson, J. P. & Jacobs, J. W. 2007 Experimental study of the single-mode three-dimensional Rayleigh–Taylor instability. Phys. Fluids 19, 124102.Google Scholar
Youngs, D. L. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
Zaytsev, S. G., Krivets, V. V., Mazilin, I. M., Titov, S. N., Chebotareva, E. I., Nikishin, V. V., Tishkin, V. F., Bouquet, S. & Haas, J.-F. 2003 Evolution of the Rayleigh–Taylor instability in the mixing zone between gases of different densities in a field of variable acceleration. Laser Part. Beams 21 (3), 393–402.Google Scholar
Zhang, Q. 1998 Analytical solutions of Layzer-type approach to unstable interfacial fluid mixing. Phys. Rev. Lett. 81 (16), 3391–3394.CrossRefGoogle Scholar
Zhou, Y., Robey, H. F. & Buckingham, A. C. 2003 Onset of turbulence in accelerated high-Reynolds-number flow. Phys. Rev. E 67 (5), 056305.Google Scholar