Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-27T16:25:08.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of the turbulent/non-turbulent interface in boundary layers

Published online by Cambridge University Press:  26 July 2016

Guillem Borrell  and
Javier Jiménez
Guillem Borrell*
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros, 3; 28040 Madrid, Spain
Javier Jiménez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros, 3; 28040 Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

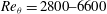The turbulent/non-turbulent interface is analysed in a direct numerical simulation of a boundary layer in the Reynolds number range $Re_{{\it\theta}}=2800{-}6600$, with emphasis on the behaviour of the relatively large-scale fractal intermittent region. This requires the introduction of a new definition of the distance between a point and a general surface, which is compared with the more usual vertical distance to the top of the layer. Interfaces are obtained by thresholding the enstrophy field and the magnitude of the rate-of-strain tensor, and it is concluded that, while the former are physically relevant features, the latter are not. By varying the threshold, a topological transition is identified as the interface moves from the free stream into the turbulent core. A vorticity scale is defined which collapses that transition for different Reynolds numbers, roughly equivalent to the root-mean-squared vorticity at the edge of the boundary layer. Conditionally averaged flow variables are analysed as functions of the new distance, both within and outside the interface. It is found that the interface contains a non-equilibrium layer whose thickness scales well with the Taylor microscale, enveloping a self-similar layer spanning a fixed fraction of the boundary-layer thickness. Interestingly, the straining structure of the flow is similar in both regions. Irrotational pockets within the turbulent core are also studied. They form a self-similar set whose size decreases with increasing depth, presumably due to breakup by the turbulence, but the rate of viscous diffusion is independent of the pocket size. The raw data used in the analysis are freely available from our web page (http://torroja.dmt.upm.es).

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 554 - 596
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arya, S., Mount, D. M., Netanyahu, N. S., Silverman, R. & Wu, A. Y. 1998 An optimal algorithm for approximate nearest neighbor searching in fixed dimensions. J. ACM 45 (6), 891–923.Google Scholar
Atkinson, C., Hackl, J., Stegeman, P., Borrell, G. & Soria, J. 2014 Numerical issues in Lagrangian tracking and topological evolution of fluid particles in wall-bounded turbulent flows. J. Phys. 506, 012003.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Borrell, G., Sillero, J. A. & Jiménez, J. 2013 A code for direct numerical simulation of turbulent boundary layers at high Reynolds numbers in BG/P supercomputers. Comput. Fluids 80, 37–43.CrossRefGoogle Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.CrossRefGoogle Scholar
Corrsin, S.1943 Investigation of flow in an axially symmetric heated jet of air. NACA WR W-94.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. 1244.Google Scholar
Dahm, W. J. A. & Dimotakis, P. E. 1987 Measurements of entrainment and mixing in turbulent jets. AIAA J. 25, 1216–1223.CrossRefGoogle Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.CrossRefGoogle Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27 (5), 055103.CrossRefGoogle Scholar
Ferre, J. A., Mumford, J. C., Savill, A. M. & Giralt, F. 1990 Three-dimensional large-eddy motions and fine-scale activity in a plane turbulent wake. J. Fluid Mech. 210, 371–414.CrossRefGoogle Scholar
Fiedler, H. E. & Head, M. R. 1966 Intermittency measurements in the turbulent boundary layer. J. Fluid Mech. 25, 719–735.CrossRefGoogle Scholar
Gampert, M., Boschung, J., Hennig, F., Gauding, M. & Peters, N. 2014 The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface. J. Fluid Mech. 750, 578–596.CrossRefGoogle Scholar
Gampert, M., Narayanaswamy, V., Schaefer, P. & Peters, N. 2013 Conditional statistics of the turbulent/non-turbulent interface in a jet flow. J. Fluid Mech. 731, 615–638.CrossRefGoogle Scholar
Gartshore, I. S. 1966 An experimental examination of the large-eddy equilibrium hypothesis. J. Fluid Mech. 24, 89–98.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface. Phys. Fluids 19 (7), 071702.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Lüthi, B., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 598, 465–475.CrossRefGoogle Scholar
Hunt, J. C. R. & Durbin, P. A. 1999 Perturbed vortical layers and shear sheltering. Fluid Dyn. Res. 24, 375–404.CrossRefGoogle Scholar
Hunt, J. C. R., Eames, I. & Westerweel, J. 2006 Mechanics of inhomogeneous turbulence and interfacial layers. J. Fluid Mech. 554, 499–519.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence – DNS results. Flow Turbul. Combust. 91 (4), 895–929.CrossRefGoogle Scholar
Ishihara, T., Ogasawara, H. & Hunt, J. C. R. 2015 Analysis of conditional statistics obtained near the turbulent/non-turbulent interface of turbulent boundary layers. J. Fluid. Struct. 53, 50–57.CrossRefGoogle Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
Jones, M., Baerentzen, J. A. & Sramek, M. 2006 3D distance fields: a survey of techniques and applications. IEEE Trans. Vis. Comput. Graphics 12 (4), 581–599.CrossRefGoogle Scholar
Klebanoff, P. S.1955 Characteristics of turbulence in a boundary layer with zero pressure gradient. NACA Tech. Rep. 1247.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluids at very large Reynolds numbers. Dokl. Akad. Nauk. SSSR 30, 301–305; reprinted in Proc. R. Soc. Lond. A 434, 9–13 (1991).Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25 (4), 045103.CrossRefGoogle Scholar
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.CrossRefGoogle Scholar
Lozano-Durán, A. & Borrell, G. 2016 Algorithm 964: an efficient algorithm to compute the genus of discrete surfaces and applications to turbulent flows. TOMS 42 (4), 34.CrossRefGoogle Scholar
Mandelbrot, B. B. 1975 On the geometry of homogeneous turbulence, with stress on the fractal dimension of the iso-surfaces of scalars. J. Fluid Mech. 72, 401–416.CrossRefGoogle Scholar
Mathew, J. & Basu, A. J. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.CrossRefGoogle Scholar
Mellado, J. P., Wang, L. & Peters, N. 2009 Gradient trajectory analysis of a scalar field with external intermittency. J. Fluid Mech. 626, 333–365.CrossRefGoogle Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.CrossRefGoogle Scholar
Muja, M. & Lowe, D. G. 2014 Scalable nearest neighbor algorithms for high-dimensional data. IEEE Trans. Pattern Anal. 11, 2227–2240.CrossRefGoogle Scholar
Mungal, M. G, Karasso, P. S. & Lozano, A. 1991 The visible structure of turbulent jet diffusion flames: large-scale organization and flame tip oscillation. Combust. Sci. Technol. 76, 165–185.CrossRefGoogle Scholar
Murlis, J., Tsai, J. & Bradshaw, P. 1982 The structure of turbulent boundary layers at low Reynolds numbers. J. Fluid Mech. 122, 13–56.CrossRefGoogle Scholar
Phillips, O. M. 1955 The irrotational motion outside a free turbulent boundary. In Mathematical Proceedings of the Cambridge Philosophical Society, vol. 51, pp. 220–229. Cambridge University Press.Google Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds-number effects in numerical boundary layers. Phys. Fluids 25 (2), 021704.CrossRefGoogle Scholar
Prasad, R. R. & Sreenivasan, K. R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7 (4), 259–264.CrossRefGoogle Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.CrossRefGoogle Scholar
Russ, J. C 1994 Fractal Surfaces. Plenum Press.CrossRefGoogle Scholar
Sandham, N. D., Mungal, M. G., Broadwell, J. E. & Reynolds, W. C. 1988 Scalar entrainment in the mixing layer. In Proc. Summ. Prog., pp. 69–76. Center for Turbulence Research, Stanford University Press.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≃ 2000. Phys. Fluids 25 (10), 105102.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26, 105109.CrossRefGoogle Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014a Interfacial layers between regions of different turbulent intensity. Annu. Rev. Fluid Mech. 46, 567–590.CrossRefGoogle Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.CrossRefGoogle Scholar
da Silva, C. B., dos Reis, R. J. N. & Pereira, J. C. F. 2011 The intense vorticity structures near the turbulent/non-turbulent interface in a jet. J. Fluid Mech. 685, 165–190.CrossRefGoogle Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.CrossRefGoogle Scholar
da Silva, C. B., Taveira, R. R. & Borrell, G 2014b Characteristics of the turbulent/nonturbulent interface in boundary layers, jets and shear-free turbulence. J. Phys. 506 (1), 012015.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111 (4), 044501.CrossRefGoogle ScholarPubMed
Simens, M., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.CrossRefGoogle Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.CrossRefGoogle Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Stewart, R. W. 1956 Irrotational motion associated with free turbulent flows. J. Fluid Mech. 1 (06), 593–606.CrossRefGoogle Scholar
Taveira, R. R., Diogo, J. S., Lopes, D. C. & da Silva, C. B. 2013 Lagrangian statistics across the turbulent–nonturbulent interface in a turbulent plane jet. Phys. Rev. E 88 (4), 043001.Google Scholar
Taveira, R. R. & da Silva, C. B. 2014 Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets. Phys. Fluids 26 (2), 021702.Google Scholar
Teixeira, M. A. C. & da Silva, C. B. 2012 Turbulence dynamics near a turbulent/non-turbulent interface. J. Fluid Mech. 695, 257–287.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Townsend, A. A. 1948 Local isotropy in the turbulent wake of a cylinder. Austral. J. Sci. Res. A 1, 161–174.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2015 Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers. Phys. Fluids 27 (8), 085109.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent–nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google ScholarPubMed
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar
Westerweel, J., Hofmann, T., Fukushima, C. & Hunt, J. 2002 The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet. Exp. Fluids 33 (6), 873–878.CrossRefGoogle Scholar
Wygnanski, I. J. & Fiedler, H. E. 1970 The two-dimensional mixing region. J. Fluid Mech. 41, 327–361.CrossRefGoogle Scholar