Published online by Cambridge University Press: 19 July 2016
We study the propagation of viscous gravity currents over a thin porous substrate with finite capillary entry pressure. Near the origin, where the current is deep, propagation of the current coincides with leakage through the substrate. Near the nose of the current, where the current is thin and the fluid pressure is below the capillary entry pressure, drainage is absent. Consequently the flow can be characterised by the evolution of drainage and fluid fronts. We analyse this flow using numerical and analytical techniques combined with laboratory-scale experiments. At early times, we find that the position of both fronts evolve as 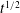 $t^{1/2}$, similar to an axisymmetric gravity current on an impermeable substrate. At later times, the growing effect of drainage inhibits spreading, causing the drainage front to logarithmically approach a steady position. In contrast, the asymptotic propagation of the fluid front is quasi-self-similar, having identical structure to the solution of gravity currents on an impermeable substrate, only with slowly varying fluid flux. We benchmark these theoretical results with laboratory experiments that are consistent with our modelling assumption, but that also highlight the detailed dynamics of drainage inhibited by finite capillary pressure.
$t^{1/2}$, similar to an axisymmetric gravity current on an impermeable substrate. At later times, the growing effect of drainage inhibits spreading, causing the drainage front to logarithmically approach a steady position. In contrast, the asymptotic propagation of the fluid front is quasi-self-similar, having identical structure to the solution of gravity currents on an impermeable substrate, only with slowly varying fluid flux. We benchmark these theoretical results with laboratory experiments that are consistent with our modelling assumption, but that also highlight the detailed dynamics of drainage inhibited by finite capillary pressure.
Videos of laboratory experiment of a viscous current propagating on a perforated surface, at the presence of finite capillary entry pressure, showing a side view of the evolving current that captures the surface current that propagates over the substrate and the detailed dynamics of the drainage inhibited by capillary pressure.