1. Introduction
The efficient absorption of water waves energy is of prime importance in mitigating their deleterious effects on coastal zones. Addressing and minimizing these impacts pose significant challenges in preserving exposed communities, ecosystems and infrastructure. In pursuit of this objective, passive systems have been proposed, falling into two sub-categories. On the one hand, we find large structures such as artificial reefs, typically constructed using concrete, rock or recycled tires (Sollitt & Cross Reference Sollitt and Cross1972; van der Meer et al. Reference van der Meer, Briganti, Zanuttigh and Wang2005; van den Brekel Reference van den Brekel2021; van Gent et al. Reference van Gent, Buis, van den Bos and Wüthrich2023) or using porous type media, including coastal vegetation, sand dunes or sedimentary layers (Zhu Reference Zhu2001; Silva, Salles & Palacio Reference Silva, Salles and Palacio2002; Barman & Bora Reference Barman and Bora2021). While these structures can efficiently absorb wave energy, they come at the cost of significant dimensions, of the order of several wavelengths. On the other hand, there are technologies designed for capturing and converting wave energy that may be small in size relative to the wavelength (Salter Reference Salter1974; Guo & Ringwood Reference Guo and Ringwood2021; Jin & Greaves Reference Jin and Greaves2021). However, they absorb only a small portion of the wave energy, as their primary purpose is energy harvesting rather than the creation of a protected zone.
In contrast to passive absorbers, devices based on active absorption aim to completely cancel outgoing waves from the device. In their classic form, developed over the last sixty years, active absorbers operate by reflection only. They are commonly referred to as ‘absorbing wavemakers’ or ‘reflection compensation systems’ and are employed to generate waves while avoiding undesired reflections, and minimizing disturbances related to artificial boundaries in wave testing facilities. The perfect absorption obtained is made possible by a destructive interference mechanism between the incident wave, whose reflection is to be cancelled, and the wave generated by the active source, i.e. the moving wall hit by the incident wave (Milgram Reference Milgram1965, Reference Milgram1970; Schäffer & Klopman Reference Schäffer and Klopman2000).
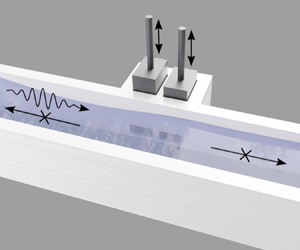
In this study, we demonstrate theoretically, numerically and experimentally that a dipole source device can be employed to achieve perfect active absorption of an incident wave in a channel, simultaneously cancelling its reflection and transmission; see figure 1. This device is inspired by the one investigated in Euvé et al. (Reference Euvé, Pham, Porter, Petitjeans, Pagneux and Maurel2023), where perfect passive absorption was achieved using two closely spaced, phase-shifted resonators, whose geometry was carefully tuned for viscous losses and resonance frequency. Here, by actively replicating the absorption conditions observed in that system, we achieve perfect absorption adaptable to any low-frequency incident wave and any loss level. To illustrate the principle of active absorption and its effectiveness, the sections of this paper are structured as follows. The theoretical formulation and numerical validation of the device principle are presented in § 2. The experimental implementation is detailed in § 3, along with an examination of the fields generated solely by the dipole source and the resulting efficient absorption in the harmonic and transient regimes. Brief conclusions are eventually drawn in § 4.

Figure 1. Perfect absorption by a dipole source. (a) Schematic view of the experimental set-up. (b) Experimental realization of the dipole source producing asymmetric wave propagation in the guide. The waves are visualized by a black line projected onto the free surface of the water, made diffusive by a white dye.
2. Perfect absorption: modelling and numerical validation
We consider the propagation of water waves within a channel characterized by width ![]() $d$ and water depth
$d$ and water depth ![]() $h$. The channel contains two extended sources positioned along one of its vertical walls, forming a dipole source that induces inflows/outflows into the channel. The two sources, rectangular and identical, have horizontal and vertical dimensions
$h$. The channel contains two extended sources positioned along one of its vertical walls, forming a dipole source that induces inflows/outflows into the channel. The two sources, rectangular and identical, have horizontal and vertical dimensions ![]() $(a, b)$, with their centres submerged at depth
$(a, b)$, with their centres submerged at depth ![]() $h_{o}$ and spaced along the
$h_{o}$ and spaced along the ![]() $x$-axis at a distance
$x$-axis at a distance ![]() $e$. Our modelling approach begins with the full three-dimensional (3-D) problem set in
$e$. Our modelling approach begins with the full three-dimensional (3-D) problem set in ![]() $\varOmega =\{x\in (-\infty,+\infty ),y\in (0,d),z\in (-h,0)\}$, with the origin at the mean free surface, and
$\varOmega =\{x\in (-\infty,+\infty ),y\in (0,d),z\in (-h,0)\}$, with the origin at the mean free surface, and ![]() $z$ directed vertically upwards. Assuming an inviscid, incompressible fluid and irrotational motion, the velocity potential
$z$ directed vertically upwards. Assuming an inviscid, incompressible fluid and irrotational motion, the velocity potential ![]() $\phi (\boldsymbol {r},t)$ and associated velocity
$\phi (\boldsymbol {r},t)$ and associated velocity ![]() $\boldsymbol {u}(\boldsymbol {r},t)$ satisfy
$\boldsymbol {u}(\boldsymbol {r},t)$ satisfy
 \begin{equation} \text{3-D problem} \quad \left\{\begin{array}{@{}l}
\displaystyle \boldsymbol{u}=\boldsymbol{\nabla} \phi,\quad
\boldsymbol{\nabla}\boldsymbol{\cdot}
\boldsymbol{u}=0,\quad\text{in } \varOmega, \\
\displaystyle
{u_z}_{|z=0}=-\dfrac{1}{g}\,\dfrac{\partial^2
\phi}{\partial t^2}_{|z=0},\quad\displaystyle
{u_z}_{|z=-h}=0, \\ \displaystyle
{u_y}_{|\varGamma}=0,\quad{u_y}_{|\varGamma_i}=U_i,
\quad i=1,2, \end{array}\right.
\end{equation}
\begin{equation} \text{3-D problem} \quad \left\{\begin{array}{@{}l}
\displaystyle \boldsymbol{u}=\boldsymbol{\nabla} \phi,\quad
\boldsymbol{\nabla}\boldsymbol{\cdot}
\boldsymbol{u}=0,\quad\text{in } \varOmega, \\
\displaystyle
{u_z}_{|z=0}=-\dfrac{1}{g}\,\dfrac{\partial^2
\phi}{\partial t^2}_{|z=0},\quad\displaystyle
{u_z}_{|z=-h}=0, \\ \displaystyle
{u_y}_{|\varGamma}=0,\quad{u_y}_{|\varGamma_i}=U_i,
\quad i=1,2, \end{array}\right.
\end{equation}
where ![]() $g$ is the gravitational constant,
$g$ is the gravitational constant, ![]() $t$ is time, and
$t$ is time, and ![]() $\boldsymbol {r}=(x,y,z)$. We have defined the surfaces
$\boldsymbol {r}=(x,y,z)$. We have defined the surfaces ![]() $\varGamma _i$,
$\varGamma _i$, ![]() $i=1,2$, and
$i=1,2$, and ![]() $\varGamma$ as
$\varGamma$ as
 \begin{equation} \left.\begin{gathered} \varGamma_1=\{(x+e/2)\in(-a/2,a/2), y=d, (z-h_{o})\in(-b/2,b/2)\},\\ \varGamma_2=\{(x-e/2)\in(-a/2,a/2), y=d, (z-h_{o})\in(-b/2,b/2)\},\\ \varGamma=\{x\in(-\infty,\infty),y\in\{0,d\},z\in(-h,0)\}\setminus (\varGamma_1\cup\varGamma_2), \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \varGamma_1=\{(x+e/2)\in(-a/2,a/2), y=d, (z-h_{o})\in(-b/2,b/2)\},\\ \varGamma_2=\{(x-e/2)\in(-a/2,a/2), y=d, (z-h_{o})\in(-b/2,b/2)\},\\ \varGamma=\{x\in(-\infty,\infty),y\in\{0,d\},z\in(-h,0)\}\setminus (\varGamma_1\cup\varGamma_2), \end{gathered}\right\} \end{equation}which correspond respectively to the regions of the vertical walls occupied by the two sources and the rigid regions of the vertical walls.
2.1. Reduction of the model: the two-dimensional problem
In the harmonic regime with time dependence ![]() ${\rm e}^{-{\rm i}\omega t}$, we go from the 3-D problem to a two-dimensional (2-D) reduced problem. To achieve this, we employ the modal representation of the 3-D solution
${\rm e}^{-{\rm i}\omega t}$, we go from the 3-D problem to a two-dimensional (2-D) reduced problem. To achieve this, we employ the modal representation of the 3-D solution
where
such that
Rearranging (2.3) into (2.1) and projecting onto ![]() $f_0(z)$ results in a 2-D problem satisfied by
$f_0(z)$ results in a 2-D problem satisfied by ![]() $\varphi (x,y)=\varphi _0(x,y)$ in
$\varphi (x,y)=\varphi _0(x,y)$ in ![]() $\varSigma =\{x\in (-\infty,+\infty ),y\in (0,d)\}$ (and we also note
$\varSigma =\{x\in (-\infty,+\infty ),y\in (0,d)\}$ (and we also note ![]() $k=k_0$ as the real-valued wavenumber of the propagating water waves) of the form
$k=k_0$ as the real-valued wavenumber of the propagating water waves) of the form
 \begin{equation} \text{2-D problem}\quad \left\{\begin{array}{@{}l} \displaystyle \Delta \varphi +k^2\varphi=0,\quad\text{in } \varSigma, \\ \displaystyle\dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma}=0,\quad\displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma_i}=u_i, \quad i=1,2, \end{array}\right. \end{equation}
\begin{equation} \text{2-D problem}\quad \left\{\begin{array}{@{}l} \displaystyle \Delta \varphi +k^2\varphi=0,\quad\text{in } \varSigma, \\ \displaystyle\dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma}=0,\quad\displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma_i}=u_i, \quad i=1,2, \end{array}\right. \end{equation}where
 \begin{equation} \left.\begin{gathered} \gamma_1=\{(x+e/2)\in(-a/2,a/2), y=d\}, \quad \gamma_2=\{(x-e/2)\in(-a/2,a/2), y=d\}, \\ \gamma=\{x\in(-\infty,\infty),y\in\{0,d\}\}\setminus (\gamma_1\cup\gamma_2), \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \gamma_1=\{(x+e/2)\in(-a/2,a/2), y=d\}, \quad \gamma_2=\{(x-e/2)\in(-a/2,a/2), y=d\}, \\ \gamma=\{x\in(-\infty,\infty),y\in\{0,d\}\}\setminus (\gamma_1\cup\gamma_2), \end{gathered}\right\} \end{equation}and
We consider an incident wave propagating to the right, characterized by a complex amplitude ![]() $\varphi _{inc}$ and sufficiently low frequency such that
$\varphi _{inc}$ and sufficiently low frequency such that ![]() $k d< 2{\rm \pi}$, implying that only one mode, independent of
$k d< 2{\rm \pi}$, implying that only one mode, independent of ![]() $y$, is propagating in the 2-D guide. Accordingly, the solution of (2.6) away from the dipole source takes the form
$y$, is propagating in the 2-D guide. Accordingly, the solution of (2.6) away from the dipole source takes the form
 \begin{equation} \left.\begin{array}{ll@{}} \varphi(x,y)\simeq \varphi_{inc}\,{\rm e}^{{\rm i}k x}+\varphi^{-}\,{\rm e}^{-{\rm i}k x}, & x\to -\infty,\\ \varphi(x,y)\simeq \varphi^+\,{\rm e}^{{\rm i}k x}, & x\to +\infty, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{ll@{}} \varphi(x,y)\simeq \varphi_{inc}\,{\rm e}^{{\rm i}k x}+\varphi^{-}\,{\rm e}^{-{\rm i}k x}, & x\to -\infty,\\ \varphi(x,y)\simeq \varphi^+\,{\rm e}^{{\rm i}k x}, & x\to +\infty, \end{array}\right\} \end{equation}
where ![]() $\varphi ^{-}$ and
$\varphi ^{-}$ and ![]() $\varphi ^+$ represent the complex amplitudes of left and right outgoing waves, respectively. The 2-D problem (2.6) can be solved explicitly. In particular, simple expressions for
$\varphi ^+$ represent the complex amplitudes of left and right outgoing waves, respectively. The 2-D problem (2.6) can be solved explicitly. In particular, simple expressions for ![]() $(\varphi ^{-},\varphi ^+)$ in (2.9) are obtained through Green's identity, as elaborated in Appendix A. They read
$(\varphi ^{-},\varphi ^+)$ in (2.9) are obtained through Green's identity, as elaborated in Appendix A. They read
 \begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle \varphi^{-}= \dfrac{{\rm i}\sin(ka/2)}{k^2d}\left(u_1\,{\rm e}^{-{\rm i}ke/2}+u_2\,{\rm e}^{{\rm i}ke/2}\right),\\ \displaystyle \varphi^+=\varphi_{inc}+\varphi^+_0,\quad \varphi^+_0= \dfrac{{\rm i}\sin(ka/2)}{k^2d}\left(u_1\,{\rm e}^{{\rm i}ke/2}+u_2\,{\rm e}^{-{\rm i}ke/2}\right). \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle \varphi^{-}= \dfrac{{\rm i}\sin(ka/2)}{k^2d}\left(u_1\,{\rm e}^{-{\rm i}ke/2}+u_2\,{\rm e}^{{\rm i}ke/2}\right),\\ \displaystyle \varphi^+=\varphi_{inc}+\varphi^+_0,\quad \varphi^+_0= \dfrac{{\rm i}\sin(ka/2)}{k^2d}\left(u_1\,{\rm e}^{{\rm i}ke/2}+u_2\,{\rm e}^{-{\rm i}ke/2}\right). \end{array}\right\} \end{equation} We will now establish the conditions on ![]() $(u_1,u_2)$ necessary to achieve perfect absorption of the incident wave, i.e. to ensure that
$(u_1,u_2)$ necessary to achieve perfect absorption of the incident wave, i.e. to ensure that ![]() $\varphi ^{-}=\varphi ^+=0$. We can already note a specific scenario when
$\varphi ^{-}=\varphi ^+=0$. We can already note a specific scenario when ![]() $ka=2n{\rm \pi}$, where
$ka=2n{\rm \pi}$, where ![]() $n$ is an integer, and
$n$ is an integer, and ![]() $kd<{\rm \pi}$. In this case,
$kd<{\rm \pi}$. In this case, ![]() $\varphi ^{-}=\varphi ^+_0=0$ regardless of the value of
$\varphi ^{-}=\varphi ^+_0=0$ regardless of the value of ![]() $\varphi _{inc}$ and the values of
$\varphi _{inc}$ and the values of ![]() $u_1$ and
$u_1$ and ![]() $u_2$. These solutions satisfy
$u_2$. These solutions satisfy ![]() $\varphi \to 0$ as
$\varphi \to 0$ as ![]() $x\to \pm \infty$ with
$x\to \pm \infty$ with ![]() $\partial _y\varphi$ remaining constant along
$\partial _y\varphi$ remaining constant along ![]() $\gamma _i$, where
$\gamma _i$, where ![]() $i=1$ or 2, and they are associated with the superposition of two localized eigenmodes; see Appendix B. Note that this particular scenario renders the sources inactive regarding the incident wave, with
$i=1$ or 2, and they are associated with the superposition of two localized eigenmodes; see Appendix B. Note that this particular scenario renders the sources inactive regarding the incident wave, with ![]() $\varphi ^{-}=0$ and
$\varphi ^{-}=0$ and ![]() $\varphi ^+=\varphi _{inc}$ whatever the values of
$\varphi ^+=\varphi _{inc}$ whatever the values of ![]() $(u_1,u_2)$. Then for
$(u_1,u_2)$. Then for ![]() $ka\neq 2 n{\rm \pi}$,
$ka\neq 2 n{\rm \pi}$, ![]() $\varphi ^{-}=0$ is obtained from (2.10) if
$\varphi ^{-}=0$ is obtained from (2.10) if ![]() $(u_1,u_2)$ satisfy the relation
$(u_1,u_2)$ satisfy the relation
which remains valid regardless of the presence or absence of an incoming wave in the guide. Subsequently, in the presence of an incoming wave and when the above condition is met, ![]() $\varphi ^+=0$ is possible if condition
$\varphi ^+=0$ is possible if condition
is also satisfied. Once again, we notice a specific scenario when ![]() $ke=n{\rm \pi}$, where
$ke=n{\rm \pi}$, where ![]() $n$ is an integer. In these cases, the solutions satisfy
$n$ is an integer. In these cases, the solutions satisfy ![]() $\varphi \to 0$ as
$\varphi \to 0$ as ![]() $x\to \pm \infty$ and either (i)
$x\to \pm \infty$ and either (i) ![]() $\partial _y\varphi =C$ along
$\partial _y\varphi =C$ along ![]() $\gamma _1$, and
$\gamma _1$, and ![]() $\partial _y\varphi =-C$ along
$\partial _y\varphi =-C$ along ![]() $\gamma _2$, or (ii)
$\gamma _2$, or (ii) ![]() $\partial _y\varphi =C$ along
$\partial _y\varphi =C$ along ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$, where
$\gamma _2$, where ![]() $C$ is a constant. Similar to the previous scenario, these solutions are associated with localized eigenmodes (see Appendix B) and inactive sources with
$C$ is a constant. Similar to the previous scenario, these solutions are associated with localized eigenmodes (see Appendix B) and inactive sources with ![]() $\varphi ^{-}=0$ and
$\varphi ^{-}=0$ and ![]() $\varphi ^+=\varphi _{inc}$.
$\varphi ^+=\varphi _{inc}$.
2.2. Numerical validation of the model
In this subsection, we inspect the validity of the model by comparisons with direct numerics. The numerical computations are performed using the PDE tool in Matlab, which employs the finite element method to solve partial differential equations. We consider the geometry depicted in figure 2, and apply radiation conditions at the ends of the guide ![]() $x=\pm x_{M}$, consistent with (2.9) for
$x=\pm x_{M}$, consistent with (2.9) for ![]() $x_{M}\gg (a+e)/2$. Specifically, we impose
$x_{M}\gg (a+e)/2$. Specifically, we impose ![]() $\partial _x\varphi + \textrm {i}k\varphi =2\textrm {i}k\varphi _{inc}\,\textrm {e}^{\textrm {i}kx_{M}}$ at
$\partial _x\varphi + \textrm {i}k\varphi =2\textrm {i}k\varphi _{inc}\,\textrm {e}^{\textrm {i}kx_{M}}$ at ![]() $x=-x_{M}$, and
$x=-x_{M}$, and ![]() $\partial _x\varphi - \textrm {i}k\varphi =0$ at
$\partial _x\varphi - \textrm {i}k\varphi =0$ at ![]() $x=x_{M}$, consistent with (2.9).
$x=x_{M}$, consistent with (2.9).

Figure 2. The two-dimensional reduced problem with extended sources considered in the numerics.
To begin with, we consider the amplitudes ![]() $(\varphi ^{-},\varphi ^+_0)$ generated solely by the sources; in the model, they are determined by (2.10) with
$(\varphi ^{-},\varphi ^+_0)$ generated solely by the sources; in the model, they are determined by (2.10) with ![]() $\varphi _{inc}=0$. Figure 3 shows the variations of these quantities, normalized to
$\varphi _{inc}=0$. Figure 3 shows the variations of these quantities, normalized to ![]() $(au_1)$, against the phase and amplitude of
$(au_1)$, against the phase and amplitude of ![]() $(u_2/u_1)$, from direct numerics (figures 3a,b) and from the model, (2.10) (figures 3c,d). The agreement between the two sets of results is excellent, showing a relative discrepancy of only 0.1 % (we have considered
$(u_2/u_1)$, from direct numerics (figures 3a,b) and from the model, (2.10) (figures 3c,d). The agreement between the two sets of results is excellent, showing a relative discrepancy of only 0.1 % (we have considered ![]() $kd={\rm \pi} /2$,
$kd={\rm \pi} /2$, ![]() $ka={\rm \pi} /4$ and
$ka={\rm \pi} /4$ and ![]() $ke={\rm \pi} /4$). Numerically, this representation for
$ke={\rm \pi} /4$). Numerically, this representation for ![]() $\varphi _{inc}=0$ is sufficient to determine the couple
$\varphi _{inc}=0$ is sufficient to determine the couple ![]() $(u_1,u_2)$ capable of achieving perfect absorption
$(u_1,u_2)$ capable of achieving perfect absorption ![]() $\varphi ^{-}=\varphi ^+=0$. We begin by determining
$\varphi ^{-}=\varphi ^+=0$. We begin by determining ![]() $\xi =u_2/u_1$ that yields
$\xi =u_2/u_1$ that yields ![]() $\varphi ^{-}=0$, since this condition is independent of the value of
$\varphi ^{-}=0$, since this condition is independent of the value of ![]() $\varphi _{inc}$. In figure 3,
$\varphi _{inc}$. In figure 3, ![]() $\varphi ^{-}=0$ is obtained for
$\varphi ^{-}=0$ is obtained for ![]() $\xi =\textrm {e}^{2.36\textrm {i}}$ (white cross), aligning well with (2.11). We then determine the value of
$\xi =\textrm {e}^{2.36\textrm {i}}$ (white cross), aligning well with (2.11). We then determine the value of ![]() $\chi =-\varphi ^+_0/(au_1)$ for
$\chi =-\varphi ^+_0/(au_1)$ for ![]() $u_2/u_1=\xi$. Eventually, in the presence of any incident wave
$u_2/u_1=\xi$. Eventually, in the presence of any incident wave ![]() $\varphi _{inc}$, the condition
$\varphi _{inc}$, the condition ![]() $\varphi ^+=0$ is obtained simply by linearity when
$\varphi ^+=0$ is obtained simply by linearity when ![]() $\varphi _{inc}/(au_1)=\chi$. In the case reported in figure 3, we obtain
$\varphi _{inc}/(au_1)=\chi$. In the case reported in figure 3, we obtain ![]() $\chi \simeq 0.44\,\textrm {e}^{-0.4\textrm {i}}$, demonstrating again good agreement with the model; see (2.12). We notice that in practice, for any incident wave
$\chi \simeq 0.44\,\textrm {e}^{-0.4\textrm {i}}$, demonstrating again good agreement with the model; see (2.12). We notice that in practice, for any incident wave ![]() $\varphi _{inc}$, perfect absorption is achieved by imposing
$\varphi _{inc}$, perfect absorption is achieved by imposing

Figure 3. Validation of the model – wave amplitudes of the outgoing waves ![]() $(\varphi ^{-},\varphi ^+)$ normalized to
$(\varphi ^{-},\varphi ^+)$ normalized to ![]() $(a u_1)$ as a function of the source amplitude ratio
$(a u_1)$ as a function of the source amplitude ratio ![]() $u_2/u_1$ (modulus and phase) obtained numerically and theoretically for
$u_2/u_1$ (modulus and phase) obtained numerically and theoretically for ![]() $\varphi _{inc}=0$. The white crosses indicate the theoretical prediction for
$\varphi _{inc}=0$. The white crosses indicate the theoretical prediction for ![]() $\varphi ^{-}=0$ from (2.11). The parameters are
$\varphi ^{-}=0$ from (2.11). The parameters are ![]() $kd={\rm \pi} /2$,
$kd={\rm \pi} /2$, ![]() $ka={\rm \pi} /4$ and
$ka={\rm \pi} /4$ and ![]() $ke={\rm \pi} /4$.
$ke={\rm \pi} /4$.
The above relations involve ![]() $(\xi,\chi )$, which depend on the frequency and on the geometry of the guide through
$(\xi,\chi )$, which depend on the frequency and on the geometry of the guide through ![]() $(ka,ke, kd)$. Numerically, they are determined from the analysis of representations as those of figure 3; theoretically, they are given by
$(ka,ke, kd)$. Numerically, they are determined from the analysis of representations as those of figure 3; theoretically, they are given by
Results in figure 4 showcase variations of ![]() $(\xi,\chi )$ determined numerically as a function the non-dimensional distance between the two sources
$(\xi,\chi )$ determined numerically as a function the non-dimensional distance between the two sources ![]() $ke \in (0,2{\rm \pi} )$ (with
$ke \in (0,2{\rm \pi} )$ (with ![]() $kd={\rm \pi} /2$ and
$kd={\rm \pi} /2$ and ![]() $ka={\rm \pi} /4$), the source extension
$ka={\rm \pi} /4$), the source extension ![]() $ka \in (0,2.5{\rm \pi} )$ (with
$ka \in (0,2.5{\rm \pi} )$ (with ![]() $kd={\rm \pi} /2$ and
$kd={\rm \pi} /2$ and ![]() $ke=2.5{\rm \pi}$), and the channel width
$ke=2.5{\rm \pi}$), and the channel width ![]() $kd \in (0,{\rm \pi} )$ (with
$kd \in (0,{\rm \pi} )$ (with ![]() $ka={\rm \pi} /4$ and
$ka={\rm \pi} /4$ and ![]() $ke={\rm \pi} /4$). The theoretical predictions (2.13a,b) are represented by solid lines for comparison, showing excellent agreement over large ranges of the parameters. It is noteworthy that for small
$ke={\rm \pi} /4$). The theoretical predictions (2.13a,b) are represented by solid lines for comparison, showing excellent agreement over large ranges of the parameters. It is noteworthy that for small ![]() $ke$, implying small
$ke$, implying small ![]() $ka$ (figure 4a), the two sources producing perfect absorption are nearly in phase opposition, hence they indeed behave as a dipole source. We also encounter the specific scenarios of inactive sources
$ka$ (figure 4a), the two sources producing perfect absorption are nearly in phase opposition, hence they indeed behave as a dipole source. We also encounter the specific scenarios of inactive sources ![]() $\varphi ^{-}=\varphi ^+_0=0$, hence
$\varphi ^{-}=\varphi ^+_0=0$, hence ![]() $\varphi _{inc}=0$, for
$\varphi _{inc}=0$, for ![]() $ke={\rm \pi}$ or for
$ke={\rm \pi}$ or for ![]() $ka=2{\rm \pi}$.
$ka=2{\rm \pi}$.

Figure 4. Numerical results – influence of the geometry on the conditions for perfect absorption. Source amplitude ratio ![]() $\xi =u_2/u_1$ (modulus and phase) and relative incident wave amplitude
$\xi =u_2/u_1$ (modulus and phase) and relative incident wave amplitude ![]() $\chi =\varphi _{inc}/(a u_1)$ (modulus and phase) against the geometrical parameters: (a,b) the distance between the sources
$\chi =\varphi _{inc}/(a u_1)$ (modulus and phase) against the geometrical parameters: (a,b) the distance between the sources ![]() $ke$ (fixing
$ke$ (fixing ![]() $kd={\rm \pi} /2$ and
$kd={\rm \pi} /2$ and ![]() $ka={\rm \pi} /4$); (c,d) the source size
$ka={\rm \pi} /4$); (c,d) the source size ![]() $ka$ (
$ka$ (![]() $kd={\rm \pi} /2$ and
$kd={\rm \pi} /2$ and ![]() $ke=2.5{\rm \pi}$); and (e,f) the channel width
$ke=2.5{\rm \pi}$); and (e,f) the channel width ![]() $kd$ (
$kd$ (![]() $ka={\rm \pi} /4$ and
$ka={\rm \pi} /4$ and ![]() $ke={\rm \pi} /4$). The markers correspond to the numerical results, and the curves to the theoretical model.
$ke={\rm \pi} /4$). The markers correspond to the numerical results, and the curves to the theoretical model.
3. Experimental realization of the active absorption
In our experiments, we use a channel with width ![]() $d=50$ mm and length 1.2 m, maintaining a fixed water depth
$d=50$ mm and length 1.2 m, maintaining a fixed water depth ![]() $h=26$ mm. The dipole source is implemented by drilling two submerged openings on one of the vertical walls of the channel, each opening having width
$h=26$ mm. The dipole source is implemented by drilling two submerged openings on one of the vertical walls of the channel, each opening having width ![]() $a=20$ mm and height
$a=20$ mm and height ![]() $b =10$ mm. The two openings are separated by a distance 5 mm (hence
$b =10$ mm. The two openings are separated by a distance 5 mm (hence ![]() $e=25$ mm) and placed at depth
$e=25$ mm) and placed at depth ![]() $h_o=16$ mm (see figure 1). Each opening is connected to a cavity producing a controlled flux through its horizontal surface
$h_o=16$ mm (see figure 1). Each opening is connected to a cavity producing a controlled flux through its horizontal surface ![]() $S_p=19\times 19\ \textrm {{mm}}^2$, with the flux created by the vertical motions of a rectangular piston with the same surface area, and controlled by a linear motor.
$S_p=19\times 19\ \textrm {{mm}}^2$, with the flux created by the vertical motions of a rectangular piston with the same surface area, and controlled by a linear motor.
We measure the fields of the free surface elevation ![]() $\hat {\eta }(x,y,t)$ using an optical method known as Fourier transform profilometry (Cobelli et al. Reference Cobelli, Maurel, Pagneux and Petitjeans2009; Maurel et al. Reference Maurel, Cobelli, Pagneux and Petitjeans2009). This method relies on acquiring and analysing the fringe patterns projected onto the water surface, with the water rendered diffusive by the addition of a dye (Przadka et al. Reference Przadka, Cabane, Pagneux, Maurel and Petitjeans2012). Eventually, reflections at the free ends of the channel are minimized by using 5-degree sloping beaches. In scenarios without an incident wave in the channel (
$\hat {\eta }(x,y,t)$ using an optical method known as Fourier transform profilometry (Cobelli et al. Reference Cobelli, Maurel, Pagneux and Petitjeans2009; Maurel et al. Reference Maurel, Cobelli, Pagneux and Petitjeans2009). This method relies on acquiring and analysing the fringe patterns projected onto the water surface, with the water rendered diffusive by the addition of a dye (Przadka et al. Reference Przadka, Cabane, Pagneux, Maurel and Petitjeans2012). Eventually, reflections at the free ends of the channel are minimized by using 5-degree sloping beaches. In scenarios without an incident wave in the channel (![]() $\eta _{inc}=0$), two beaches are positioned at the left and right ends of the channel. In the presence of an incident wave generated by a wavemaker at the left end of the channel, a single beach is used (at the right end of the channel).
$\eta _{inc}=0$), two beaches are positioned at the left and right ends of the channel. In the presence of an incident wave generated by a wavemaker at the left end of the channel, a single beach is used (at the right end of the channel).
3.1. Active absorption in the harmonic regime
In the harmonic regime, we proceed by controlling the two pistons independently at frequency ![]() $\omega$ and amplitudes
$\omega$ and amplitudes ![]() $p_1$ and
$p_1$ and ![]() $p_2$. The conservation of fluxes implies that the mean velocities
$p_2$. The conservation of fluxes implies that the mean velocities ![]() $U_n$, where
$U_n$, where ![]() $n=1,2$, satisfy
$n=1,2$, satisfy ![]() $-\textrm {i}\omega p_nS_p=ab U_n$. Consequently, from (2.8a,b) the velocities
$-\textrm {i}\omega p_nS_p=ab U_n$. Consequently, from (2.8a,b) the velocities ![]() $u_n$ used in the 2-D model are given approximatively by
$u_n$ used in the 2-D model are given approximatively by
with ![]() $\alpha$ defined in (2.8a,b). Next, the measured field of the free surface elevation
$\alpha$ defined in (2.8a,b). Next, the measured field of the free surface elevation ![]() $\hat \eta (x,y,t)$ provides
$\hat \eta (x,y,t)$ provides ![]() $\eta (x,y)$ by Fourier transform, namely
$\eta (x,y)$ by Fourier transform, namely
with ![]() $T$ covering several periods (typically 20), and we now seek solutions in the far field of the form
$T$ covering several periods (typically 20), and we now seek solutions in the far field of the form
 \begin{equation} \left.\begin{array}{ll@{}} \eta(x,y)\simeq \eta_{inc}\,{\rm e}^{{\rm i}k x}+\eta^-\,{\rm e}^{-{\rm i}k x}, & x\to -\infty,\\ \eta(x,y)\simeq \eta^+\,{\rm e}^{{\rm i}k x}, & x\to +\infty, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{ll@{}} \eta(x,y)\simeq \eta_{inc}\,{\rm e}^{{\rm i}k x}+\eta^-\,{\rm e}^{-{\rm i}k x}, & x\to -\infty,\\ \eta(x,y)\simeq \eta^+\,{\rm e}^{{\rm i}k x}, & x\to +\infty, \end{array}\right\} \end{equation}
as in (2.9). With ![]() $\hat \eta (x,y,t)=-(1/g)\,\partial _t\phi (x,y,0,t)$, and utilizing (2.3), (2.10) and (3.1), the complex amplitudes
$\hat \eta (x,y,t)=-(1/g)\,\partial _t\phi (x,y,0,t)$, and utilizing (2.3), (2.10) and (3.1), the complex amplitudes ![]() $(\eta ^-,\eta ^+)$ can be written as
$(\eta ^-,\eta ^+)$ can be written as
 \begin{equation} \left.\begin{array}{@{}c@{}} \eta^-= {\rm i}\beta \left(p_1\,{\rm e}^{-{\rm i}ke/2}+p_2\,{\rm e}^{{\rm i}ke/2}\right),\\ \eta^+=\eta_{inc}+\eta^+_0,\quad \eta^+_0={\rm i}\beta\left(p_1\,{\rm e}^{{\rm i}ke/2}+p_2\,{\rm e}^{-{\rm i}ke/2}\right), \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} \eta^-= {\rm i}\beta \left(p_1\,{\rm e}^{-{\rm i}ke/2}+p_2\,{\rm e}^{{\rm i}ke/2}\right),\\ \eta^+=\eta_{inc}+\eta^+_0,\quad \eta^+_0={\rm i}\beta\left(p_1\,{\rm e}^{{\rm i}ke/2}+p_2\,{\rm e}^{-{\rm i}ke/2}\right), \end{array}\right\} \end{equation}
with ![]() $\beta$ a non-dimensional parameter defined by
$\beta$ a non-dimensional parameter defined by
Accordingly, the conditions for perfect absorption read
which is the equivalent of (2.13a,b), with ![]() $\xi =-\textrm {e}^{-\textrm {i}ke}$ and
$\xi =-\textrm {e}^{-\textrm {i}ke}$ and ![]() $\chi _{e}=2\beta \sin (ke)\,\textrm {e}^{-\textrm {i}ke/2}$.
$\chi _{e}=2\beta \sin (ke)\,\textrm {e}^{-\textrm {i}ke/2}$.
In our first experiments, we follow the same procedure as in our numerical simulations, using ![]() $\eta _{inc}=0$, and measure the waves
$\eta _{inc}=0$, and measure the waves ![]() $\eta (x,y)$ generated by the dipole source in the harmonic regime. Following (2.13a,b), we aim to find the condition
$\eta (x,y)$ generated by the dipole source in the harmonic regime. Following (2.13a,b), we aim to find the condition ![]() $p_2=\xi p _1$ capable of experimentally producing
$p_2=\xi p _1$ capable of experimentally producing ![]() $\eta ^-=0$ and characterize the corresponding values of
$\eta ^-=0$ and characterize the corresponding values of ![]() $\chi _{e}=-\eta ^+_0/p_1$. To achieve this, we set the frequency to
$\chi _{e}=-\eta ^+_0/p_1$. To achieve this, we set the frequency to ![]() $\omega =14.5\ \textrm {rad}\ \textrm {s}^{-1}$, corresponding to
$\omega =14.5\ \textrm {rad}\ \textrm {s}^{-1}$, corresponding to ![]() $kd\simeq {\rm \pi}/2$, and conduct a series of
$kd\simeq {\rm \pi}/2$, and conduct a series of ![]() $11\times 21$ experiments with varying
$11\times 21$ experiments with varying ![]() $(p_1,p_2)$. The typical amplitude of each piston is
$(p_1,p_2)$. The typical amplitude of each piston is ![]() $p_n\sim 5$ mm. Specifically, we consider 11 values of
$p_n\sim 5$ mm. Specifically, we consider 11 values of ![]() $|p_2/p_1|\in (0, 2)$, and for each modulus ratio, we vary the relative phase of
$|p_2/p_1|\in (0, 2)$, and for each modulus ratio, we vary the relative phase of ![]() $(p_2/p_1)$ between
$(p_2/p_1)$ between ![]() $-{\rm \pi}$ and
$-{\rm \pi}$ and ![]() ${\rm \pi}$ with a step of
${\rm \pi}$ with a step of ![]() ${\rm \pi} /20$. In each experiment, we measure the entire field
${\rm \pi} /20$. In each experiment, we measure the entire field ![]() $\eta (x,y)$, and by averaging it over
$\eta (x,y)$, and by averaging it over ![]() $y$ in the far field (sufficiently distant from the source), we determine the constant complex amplitudes
$y$ in the far field (sufficiently distant from the source), we determine the constant complex amplitudes ![]() $(\eta ^-,\eta ^+_0)$. The results, depicted in figure 5, demonstrate good agreement with the theoretical model in (3.4). In particular, the agreement confirms (see white crosses in figure 5) that for
$(\eta ^-,\eta ^+_0)$. The results, depicted in figure 5, demonstrate good agreement with the theoretical model in (3.4). In particular, the agreement confirms (see white crosses in figure 5) that for ![]() $p_2/p_1=\xi =-1.03\,\textrm {e}^{-\textrm {i}0.75}\simeq -\textrm {e}^{-\textrm {i}ke}$, the left-outgoing wave vanishes (
$p_2/p_1=\xi =-1.03\,\textrm {e}^{-\textrm {i}0.75}\simeq -\textrm {e}^{-\textrm {i}ke}$, the left-outgoing wave vanishes (![]() $\eta ^-\simeq 0$), and the corresponding value
$\eta ^-\simeq 0$), and the corresponding value ![]() $\chi _{e}=-\eta ^+_0/p_1= 0.13\,\textrm {e}^{-\textrm {i}0.36}$ is consistent with (3.4).
$\chi _{e}=-\eta ^+_0/p_1= 0.13\,\textrm {e}^{-\textrm {i}0.36}$ is consistent with (3.4).

Figure 5. Amplitudes of the outgoing waves (![]() $\eta ^-,\eta ^+_0$) normalized to
$\eta ^-,\eta ^+_0$) normalized to ![]() $p_1$ as a function of the ratio
$p_1$ as a function of the ratio ![]() $p_2/p_1$ (modulus and phase) obtained experimentally and theoretically (see (3.4)) for
$p_2/p_1$ (modulus and phase) obtained experimentally and theoretically (see (3.4)) for ![]() $\eta _{inc}=0$. The white crosses indicate the theoretical prediction for
$\eta _{inc}=0$. The white crosses indicate the theoretical prediction for ![]() $\eta ^-=0$. The frequency is
$\eta ^-=0$. The frequency is ![]() $\omega =14.5\ \textrm {rad}\ \textrm {s}^{-1}$ (
$\omega =14.5\ \textrm {rad}\ \textrm {s}^{-1}$ (![]() $kd\simeq {\rm \pi}/2$).
$kd\simeq {\rm \pi}/2$).
In the next step, we quantitatively characterize the condition for perfect absorption across frequencies. Specifically, we vary the frequency within the range such that ![]() $k\in (0.2,0.7){\rm \pi} /d$ and conduct a coarse version of the analysis depicted in figure 5, employing only
$k\in (0.2,0.7){\rm \pi} /d$ and conduct a coarse version of the analysis depicted in figure 5, employing only ![]() $3\times 3$ experiments centred on the theoretical value
$3\times 3$ experiments centred on the theoretical value ![]() $p_2/p_1=-\textrm {e}^{-\textrm {i}ke}$, resulting in
$p_2/p_1=-\textrm {e}^{-\textrm {i}ke}$, resulting in ![]() $\eta ^-=0$. This is done by selecting
$\eta ^-=0$. This is done by selecting ![]() $|p_2/p_1|$ from the set
$|p_2/p_1|$ from the set ![]() $\{0.9,1,1.1\}$, and the phase of
$\{0.9,1,1.1\}$, and the phase of ![]() $(p_2/p_1)$ from
$(p_2/p_1)$ from ![]() $-ke+{\rm \pi} \{0.96,1,1.04\}$; afterwards, linear interpolations are employed to determine the optimal condition for achieving perfect absorption. By repeating this experimental procedure four times, we obtained a refined mean prediction along with error bars derived from standard deviations. The conditions for perfect absorption are depicted in figure 6, illustrating
$-ke+{\rm \pi} \{0.96,1,1.04\}$; afterwards, linear interpolations are employed to determine the optimal condition for achieving perfect absorption. By repeating this experimental procedure four times, we obtained a refined mean prediction along with error bars derived from standard deviations. The conditions for perfect absorption are depicted in figure 6, illustrating ![]() $\xi =p_2/p_1$ (both modulus and phase), yielding
$\xi =p_2/p_1$ (both modulus and phase), yielding ![]() $\eta ^-=0$, and the corresponding values of
$\eta ^-=0$, and the corresponding values of ![]() $\chi _{e}=\eta _{inc}/p_1=-\eta ^+_0/p_1$ across various frequencies. To compare with the model (3.6a,b) represented by solid lines in figure 6),
$\chi _{e}=\eta _{inc}/p_1=-\eta ^+_0/p_1$ across various frequencies. To compare with the model (3.6a,b) represented by solid lines in figure 6), ![]() $\xi$ and
$\xi$ and ![]() $\chi _{e}$ were calculated using complex wavenumbers
$\chi _{e}$ were calculated using complex wavenumbers ![]() $k\to k+\textrm {i}k_{im}$, where the small imaginary part
$k\to k+\textrm {i}k_{im}$, where the small imaginary part ![]() $k_{im}=2\times 10^{-2}\,k^2d$ accounts for attenuation due to viscous losses. This function fits the losses observed experimentally.
$k_{im}=2\times 10^{-2}\,k^2d$ accounts for attenuation due to viscous losses. This function fits the losses observed experimentally.

Figure 6. Experimental measurements – conditions for perfect absorption. Source amplitude ratio ![]() $\xi =p_2/p_1$ (modulus and phase) and relative incident wave amplitude
$\xi =p_2/p_1$ (modulus and phase) and relative incident wave amplitude ![]() $\chi _{e}=\eta _{inc}/p_1=-\eta ^+_0/p_1$ (modulus and phase) against the frequency by means of
$\chi _{e}=\eta _{inc}/p_1=-\eta ^+_0/p_1$ (modulus and phase) against the frequency by means of ![]() $kd$. The markers correspond to the experimental measurements, and the curves to the theoretical model (3.4), in which complex wavenumbers with a small imaginary part
$kd$. The markers correspond to the experimental measurements, and the curves to the theoretical model (3.4), in which complex wavenumbers with a small imaginary part ![]() $k_{im}=2\times 10^{-2}\,k^2d$ were used to account for attenuation, due to viscous losses.
$k_{im}=2\times 10^{-2}\,k^2d$ were used to account for attenuation, due to viscous losses.
Eventually, figure 7 presents experimental evidence of perfect absorption when ![]() $\eta _{inc}\neq 0$. We generated
$\eta _{inc}\neq 0$. We generated ![]() $\eta _{inc}$ at
$\eta _{inc}$ at ![]() $\omega =12.6\ \textrm {rad}\ \textrm {s}^{-1}$ (
$\omega =12.6\ \textrm {rad}\ \textrm {s}^{-1}$ (![]() $kd=0.42{\rm \pi}$) using a plunging-type wavemaker placed at the left end of the waveguide and controlled by a linear motor. The complex amplitude
$kd=0.42{\rm \pi}$) using a plunging-type wavemaker placed at the left end of the waveguide and controlled by a linear motor. The complex amplitude ![]() $\eta _{inc}$ was characterized in a preliminary study (not reported), in the absence of dipolar source (
$\eta _{inc}$ was characterized in a preliminary study (not reported), in the absence of dipolar source (![]() $\,p_1=p_2=0$). This allowed us to determine the complex amplitudes
$\,p_1=p_2=0$). This allowed us to determine the complex amplitudes ![]() $(p_1,p_2)$ producing perfect absorption, according to (3.6a,b), which was validated in figure 6. In practice, generating the incident waves and those emitted by the dipole source is achieved by synchronizing the three linear motors. Figure 7(a) displays the corresponding
$(p_1,p_2)$ producing perfect absorption, according to (3.6a,b), which was validated in figure 6. In practice, generating the incident waves and those emitted by the dipole source is achieved by synchronizing the three linear motors. Figure 7(a) displays the corresponding ![]() $\eta (x,y)$ (real part) derived from the measured field
$\eta (x,y)$ (real part) derived from the measured field ![]() $\hat {\eta }(x,y,t)$ using (3.2). For comparison, figure 7(b) presents the result obtained via numerical computation in two dimensions under the same conditions. The profile of
$\hat {\eta }(x,y,t)$ using (3.2). For comparison, figure 7(b) presents the result obtained via numerical computation in two dimensions under the same conditions. The profile of ![]() $\eta$ along
$\eta$ along ![]() $x$ reported in figure 7(c) represents an average of
$x$ reported in figure 7(c) represents an average of ![]() $\eta (x,y)$ over
$\eta (x,y)$ over ![]() $y$. It reveals weak outgoing waves, with
$y$. It reveals weak outgoing waves, with ![]() $\eta ^+$ approaching zero for
$\eta ^+$ approaching zero for ![]() $x\gtrsim 2a$, and
$x\gtrsim 2a$, and ![]() $\eta$ without the characteristic beatings indicative of the superposition of left- and right-going waves for
$\eta$ without the characteristic beatings indicative of the superposition of left- and right-going waves for ![]() $x\lesssim -2a$, hence
$x\lesssim -2a$, hence ![]() $\eta ^-\sim 0$. To further quantify the smallness of
$\eta ^-\sim 0$. To further quantify the smallness of ![]() $\eta ^-$ and
$\eta ^-$ and ![]() $\eta ^+$, fits of
$\eta ^+$, fits of ![]() $\eta$ were conducted for
$\eta$ were conducted for ![]() $x$ in the ranges
$x$ in the ranges ![]() $(-0.4,-0.05)$ cm and
$(-0.4,-0.05)$ cm and ![]() $(0.05,0.4)$ cm, utilizing
$(0.05,0.4)$ cm, utilizing ![]() $k_{im}=2\times 10^{-2}\,k^2d$ as done previously. This procedure was repeated for 11 frequencies corresponding to
$k_{im}=2\times 10^{-2}\,k^2d$ as done previously. This procedure was repeated for 11 frequencies corresponding to ![]() $kd$ in the range
$kd$ in the range ![]() $(0.2, 0.7){\rm \pi}$. The results of this series of experiments are presented in figure 7(d), confirming consistent absorption efficiency with
$(0.2, 0.7){\rm \pi}$. The results of this series of experiments are presented in figure 7(d), confirming consistent absorption efficiency with ![]() $(|\eta ^-/\eta _{inc}|^2+|\eta ^+/\eta _{inc}|^2)$ at approximately
$(|\eta ^-/\eta _{inc}|^2+|\eta ^+/\eta _{inc}|^2)$ at approximately ![]() $10^{-3}$ over the entire frequency range, signifying 99.9 % absorption.
$10^{-3}$ over the entire frequency range, signifying 99.9 % absorption.

Figure 7. (a) Real part of ![]() $\eta (x,y)$ measured experimentally, for
$\eta (x,y)$ measured experimentally, for ![]() $\omega =12.6\ \textrm {rad}\ \textrm {s}^{-1}$ (corresponding to an incident wavenumber
$\omega =12.6\ \textrm {rad}\ \textrm {s}^{-1}$ (corresponding to an incident wavenumber ![]() $kd/{\rm \pi} =0.42$). (b) Same results from direct numerics. (c) Average in
$kd/{\rm \pi} =0.42$). (b) Same results from direct numerics. (c) Average in ![]() $y$ of
$y$ of ![]() $\eta (x,y)$. (d) Left-going and right-going energies, normalized to the incident one, against the incident wavenumber
$\eta (x,y)$. (d) Left-going and right-going energies, normalized to the incident one, against the incident wavenumber ![]() $kd/{\rm \pi}$.
$kd/{\rm \pi}$.
3.2. Active absorption in the transient regime
To conclude our experimental demonstration of perfect absorption, we investigate an incoming wave signal in the transient regime. This signal is generated based on its Fourier transform ![]() $\eta _{inc}(\omega )$, randomly distributed in phase and modulus but constrained by a Gaussian profile, specifically
$\eta _{inc}(\omega )$, randomly distributed in phase and modulus but constrained by a Gaussian profile, specifically
 \begin{equation} \left.\begin{gathered} \eta_{inc}(\omega) \ \text{random with } |\eta_{inc}(\omega)|<\eta_0\exp\left({-\frac{(\omega-\omega_0)^2}{\sigma^2}}\right),\\ \hat{\eta}_{inc}(x,t)=\int_0^{\infty} \eta_{inc} (\omega)\exp({{\rm i}(kx-\omega t)})\,\text{d}\omega, \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \eta_{inc}(\omega) \ \text{random with } |\eta_{inc}(\omega)|<\eta_0\exp\left({-\frac{(\omega-\omega_0)^2}{\sigma^2}}\right),\\ \hat{\eta}_{inc}(x,t)=\int_0^{\infty} \eta_{inc} (\omega)\exp({{\rm i}(kx-\omega t)})\,\text{d}\omega, \end{gathered}\right\}\end{equation}
with parameters ![]() $\eta _0=0.08$ mm,
$\eta _0=0.08$ mm, ![]() $\omega _0=14.5\ \textrm {rad}\ \textrm {s}^{-1}$ and
$\omega _0=14.5\ \textrm {rad}\ \textrm {s}^{-1}$ and ![]() $\sigma =4\ \textrm {rad} \textrm {s}^{-1}$ (see figure 8e). In practice, we consider
$\sigma =4\ \textrm {rad} \textrm {s}^{-1}$ (see figure 8e). In practice, we consider ![]() $N=100$ discrete frequencies
$N=100$ discrete frequencies ![]() $\omega _i\in (1,30)\ \textrm {rad}\ \textrm {s}^{-1}$. Leveraging our earlier study in the harmonic regime, where we identified
$\omega _i\in (1,30)\ \textrm {rad}\ \textrm {s}^{-1}$. Leveraging our earlier study in the harmonic regime, where we identified ![]() $\eta _{inc} (\omega )/p_1(\omega )$ and
$\eta _{inc} (\omega )/p_1(\omega )$ and ![]() $p_2(\omega )/p_1(\omega )$ for perfect absorption (figure 6 and (3.6a,b)), we generate
$p_2(\omega )/p_1(\omega )$ for perfect absorption (figure 6 and (3.6a,b)), we generate ![]() $\hat {p}_1(t)$ and
$\hat {p}_1(t)$ and ![]() $\hat {p}_2(t)$ through Fourier transforms.
$\hat {p}_2(t)$ through Fourier transforms.

Figure 8. (a) Space–time diagram ![]() $\eta (x,t)$, average in
$\eta (x,t)$, average in ![]() $y$ of
$y$ of ![]() $\eta (x,y,t)$, reporting the propagation of an incident wave generated following (3.6a,b) and its interaction with the dipole source tuned to achieve perfect absorption. (b) Time signal before (at
$\eta (x,y,t)$, reporting the propagation of an incident wave generated following (3.6a,b) and its interaction with the dipole source tuned to achieve perfect absorption. (b) Time signal before (at ![]() $x=-0.2$ m) and after (at
$x=-0.2$ m) and after (at ![]() $x=0.2$ m) the dipolar source. (c,d) Space and time Fourier transforms
$x=0.2$ m) the dipolar source. (c,d) Space and time Fourier transforms ![]() ${\lvert }{\hat {\eta }(k,\omega )}{\rvert }$ calculated for
${\lvert }{\hat {\eta }(k,\omega )}{\rvert }$ calculated for ![]() $x<0$ and
$x<0$ and ![]() $x>0$, revealing vanishing outgoing waves, all the energy corresponding to the incident wave
$x>0$, revealing vanishing outgoing waves, all the energy corresponding to the incident wave ![]() $\eta _{inc}$ in alignment with the theoretical dispersion (black line in c). (e) Wave amplitude along the dispersion relation of the incident and outgoing waves.
$\eta _{inc}$ in alignment with the theoretical dispersion (black line in c). (e) Wave amplitude along the dispersion relation of the incident and outgoing waves.
The primary result is presented in figure 8(a), which illustrates a space–time diagram of the signal ![]() $\hat {\eta }(x,t)$ averaged over
$\hat {\eta }(x,t)$ averaged over ![]() $y\in (0,d)$. The effective absorption attributable to the dipole source centred at
$y\in (0,d)$. The effective absorption attributable to the dipole source centred at ![]() $x=0$ is evident. Indeed,
$x=0$ is evident. Indeed, ![]() $\hat {\eta }(x,t)$ remains constant in shape over time for any
$\hat {\eta }(x,t)$ remains constant in shape over time for any ![]() $x\lesssim -2a$ up to slight attenuation during propagation, while it is nearly zero for
$x\lesssim -2a$ up to slight attenuation during propagation, while it is nearly zero for ![]() $x\gtrsim 2a$. These characteristic shapes are illustrated for
$x\gtrsim 2a$. These characteristic shapes are illustrated for ![]() $x=-0.2$ m and
$x=-0.2$ m and ![]() $x=0.2$ m in figure 8(b). To evaluate absorption quantitatively, we analyse the amplitudes in Fourier space
$x=0.2$ m in figure 8(b). To evaluate absorption quantitatively, we analyse the amplitudes in Fourier space ![]() ${{\eta }(k,\omega )}$ in these two regions utilizing
${{\eta }(k,\omega )}$ in these two regions utilizing
 \begin{equation} \eta^\pm(k,\omega)=\int_{x_{1}^\pm}^{x_{2}^\pm}\int_{0}^{T} \hat{\eta}(x,t)\exp({{\rm i}(\omega t -kx)})\,{\text{d}}\kern0.06em x\,{\text{d}} t, \end{equation}
\begin{equation} \eta^\pm(k,\omega)=\int_{x_{1}^\pm}^{x_{2}^\pm}\int_{0}^{T} \hat{\eta}(x,t)\exp({{\rm i}(\omega t -kx)})\,{\text{d}}\kern0.06em x\,{\text{d}} t, \end{equation}
with ![]() $T=20$ s,
$T=20$ s, ![]() $(x_{1}^-,x_{2}^-)=(-0.4\ \textrm {m}, 0)$ and
$(x_{1}^-,x_{2}^-)=(-0.4\ \textrm {m}, 0)$ and ![]() $(x_{1}^+,x_{2}^+)=(0, 0.4\ \textrm {m})$ (before and after the dipole). Results in the
$(x_{1}^+,x_{2}^+)=(0, 0.4\ \textrm {m})$ (before and after the dipole). Results in the ![]() $(k,\omega )$ plane are shown in figures 8(c) and 8(d), respectively. In figure 8(c), it is notable that the spectral content of
$(k,\omega )$ plane are shown in figures 8(c) and 8(d), respectively. In figure 8(c), it is notable that the spectral content of ![]() $\eta ^-(k,\omega )$ is almost zero for
$\eta ^-(k,\omega )$ is almost zero for ![]() $k<0$, particularly along the dispersion line
$k<0$, particularly along the dispersion line ![]() $k=-k(\omega )$ (solid red line), and lies predominantly along the dispersion line
$k=-k(\omega )$ (solid red line), and lies predominantly along the dispersion line ![]() $k=k(\omega )>0$ (solid black line), hence associated with the right-going wave only. This confirms
$k=k(\omega )>0$ (solid black line), hence associated with the right-going wave only. This confirms ![]() $\eta ^-=0$. Similarly, figure 8(d) demonstrates that the spectral content of
$\eta ^-=0$. Similarly, figure 8(d) demonstrates that the spectral content of ![]() $\eta ^+(k,\omega )$ along the line
$\eta ^+(k,\omega )$ along the line ![]() $k=k(\omega )$ is nearly zero. The amplitude along each dispersion line is shown in figure 8(e). These observations are further quantified by deriving a measure of the energy of the incident, left-going and right-going waves by calculating the energies along these lines, namely
$k=k(\omega )$ is nearly zero. The amplitude along each dispersion line is shown in figure 8(e). These observations are further quantified by deriving a measure of the energy of the incident, left-going and right-going waves by calculating the energies along these lines, namely
 \begin{equation} \left.\begin{gathered} E_{inc}=\int_0^{2\omega_0}{\lvert}{{\eta}^-(+k(\omega),\omega)}{\rvert}^2 \,\text{d}\omega,\quad E^-=\int_0^{2\omega_0}{\lvert}{{\eta}^-(-k(\omega),\omega)}{\rvert}^2 \,\text{d}\omega,\\ E^+=\int_0^{2\omega_0}{\lvert}{{\eta}^+(+k(\omega),\omega)}{\rvert}^2 \,\text{d}\omega, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} E_{inc}=\int_0^{2\omega_0}{\lvert}{{\eta}^-(+k(\omega),\omega)}{\rvert}^2 \,\text{d}\omega,\quad E^-=\int_0^{2\omega_0}{\lvert}{{\eta}^-(-k(\omega),\omega)}{\rvert}^2 \,\text{d}\omega,\\ E^+=\int_0^{2\omega_0}{\lvert}{{\eta}^+(+k(\omega),\omega)}{\rvert}^2 \,\text{d}\omega, \end{gathered}\right\} \end{equation}
resulting in an absorption ![]() $(E_{inc}-E^--E^+)/E_{inc}=99.5\,\%$.
$(E_{inc}-E^--E^+)/E_{inc}=99.5\,\%$.
4. Concluding remarks
The active absorption device that we have proposed is inspired by two absorption systems. First, it takes up the concept of conventional active absorption, which traditionally works only in reflection, and is extended here to encompass both reflection and transmission, independently of viscous losses. Second, it is inspired by a passive device for which we had demonstrated a relationship between the amplitudes of the resonators and that of the incident wave leading to perfect absorption (Euvé et al. Reference Euvé, Pham, Porter, Petitjeans, Pagneux and Maurel2023). We have adopted this relationship in the active system, thus avoiding dependence on the level of loss and extending its range of frequency validity. This has been demonstrated for waves guided in a channel. It should be noted, however, that following the developments proposed for active absorbers in reflection in Schäffer & Klopman (Reference Schäffer and Klopman2000), our absorber should be applicable to unguided configurations and arbitrary incidences.
Funding
The authors acknowledge the support of the ANR under grant nos ANR-21-CE30-0046 CoProMM and ANR-19-CE08-0006 MetaReso.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Additional information on the derivation of  $(\varphi ^{-},\varphi ^+)$
$(\varphi ^{-},\varphi ^+)$
We define ![]() $\psi (x,y)$ as a test function satisfying
$\psi (x,y)$ as a test function satisfying
 \begin{equation} \left.\begin{array}{@{}c@{}} \Delta \psi +k^2\psi=0, \quad \text{in } \varSigma,\\ \displaystyle\dfrac{\partial{\psi}}{\partial{y}}_{|\gamma}=\dfrac{\partial{\psi}}{\partial{y}}_{|\gamma_i}=0, \quad i=1,2. \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} \Delta \psi +k^2\psi=0, \quad \text{in } \varSigma,\\ \displaystyle\dfrac{\partial{\psi}}{\partial{y}}_{|\gamma}=\dfrac{\partial{\psi}}{\partial{y}}_{|\gamma_i}=0, \quad i=1,2. \end{array}\right\} \end{equation} The derivation of the Green's identity proceeds as follows. First, we define the finite 2-D domain ![]() $\varSigma _{m}=\{x\in (-x_{m},x_{m}),y\in (0,d)\}$ with
$\varSigma _{m}=\{x\in (-x_{m},x_{m}),y\in (0,d)\}$ with ![]() $x_{m}>(e+a)/2$. Then we subtract the product of the first equation in (2.6) with
$x_{m}>(e+a)/2$. Then we subtract the product of the first equation in (2.6) with ![]() $\psi$ from the product of the first equation of (A1) with
$\psi$ from the product of the first equation of (A1) with ![]() $\varphi$, integrating over
$\varphi$, integrating over ![]() $\varSigma _{m}$. Employing integration by parts yields
$\varSigma _{m}$. Employing integration by parts yields
where ![]() $\partial \varSigma _{m}=\{x\in (-x_{m},x_{m}),y\in \{0,d\}\}\cup \gamma ^+\cup \gamma ^-$ with
$\partial \varSigma _{m}=\{x\in (-x_{m},x_{m}),y\in \{0,d\}\}\cup \gamma ^+\cup \gamma ^-$ with ![]() $\gamma ^\pm =\{x=\pm x_{m}, y\in (0,d)\}$. Further, taking into account the boundary conditions on
$\gamma ^\pm =\{x=\pm x_{m}, y\in (0,d)\}$. Further, taking into account the boundary conditions on ![]() $\gamma _i$,
$\gamma _i$, ![]() $i=1,2$ (along with Neumann conditions on the rigid walls), we obtain
$i=1,2$ (along with Neumann conditions on the rigid walls), we obtain
 \begin{align} &-\int_{\gamma^-}\left(\psi\,\frac{\partial{\varphi}}{\partial{x}}-\varphi\,\frac{\partial{\psi}}{\partial{x}}\right){\text{d}} y +\int_{\gamma^+}\left(\psi\,\frac{\partial{\varphi}}{\partial{x}}-\varphi\,\frac{\partial{\psi}}{\partial{x}}\right){\text{d}} y\nonumber\\ &\quad +u_1\int_{\gamma_1}\psi(x,d)\,{\text{d}}\kern0.06em x+u_2\int_{\gamma_2}\psi(x,d)\,{\text{d}}\kern0.06em x=0. \end{align}
\begin{align} &-\int_{\gamma^-}\left(\psi\,\frac{\partial{\varphi}}{\partial{x}}-\varphi\,\frac{\partial{\psi}}{\partial{x}}\right){\text{d}} y +\int_{\gamma^+}\left(\psi\,\frac{\partial{\varphi}}{\partial{x}}-\varphi\,\frac{\partial{\psi}}{\partial{x}}\right){\text{d}} y\nonumber\\ &\quad +u_1\int_{\gamma_1}\psi(x,d)\,{\text{d}}\kern0.06em x+u_2\int_{\gamma_2}\psi(x,d)\,{\text{d}}\kern0.06em x=0. \end{align}
Subsequently, setting ![]() $\psi (x,y)=\textrm {e}^{-\textrm {i}kx}$ and taking into account that
$\psi (x,y)=\textrm {e}^{-\textrm {i}kx}$ and taking into account that ![]() $\psi$ is orthogonal to the evanescent field on
$\psi$ is orthogonal to the evanescent field on ![]() $\gamma ^+$ and
$\gamma ^+$ and ![]() $\gamma ^-$, along with the far-field solution for
$\gamma ^-$, along with the far-field solution for ![]() $\varphi$ in (2.9), we obtain
$\varphi$ in (2.9), we obtain
leading to the second relation in (2.10). Analogously, repeating the calculation with ![]() $\psi (x,y)=\textrm {e}^{\textrm {i}kx}$ yields the first relation in (2.10).
$\psi (x,y)=\textrm {e}^{\textrm {i}kx}$ yields the first relation in (2.10).
Appendix B. The cases of inactive sources: existence of localized eigenmodes
Here, we revisit the concept of what we previously termed ‘inactive sources’, which, from (2.10), yield ![]() $\varphi ^{-}=\varphi ^+_0=0$ regardless of the value of
$\varphi ^{-}=\varphi ^+_0=0$ regardless of the value of ![]() $\varphi _{inc}$. First, we define the problem set for
$\varphi _{inc}$. First, we define the problem set for ![]() $\varphi _1$ that satisfies the Helmholtz equation with
$\varphi _1$ that satisfies the Helmholtz equation with ![]() $\partial _y\varphi _1=u_1$ on
$\partial _y\varphi _1=u_1$ on ![]() $\gamma _1$, and Neumann boundary conditions on
$\gamma _1$, and Neumann boundary conditions on ![]() $\gamma$ and
$\gamma$ and ![]() $\gamma _2$. We seek solutions to this problem that decay exponentially to 0 when
$\gamma _2$. We seek solutions to this problem that decay exponentially to 0 when ![]() $x\to \pm \infty$. Through integration of the Helmholtz equation over the domain
$x\to \pm \infty$. Through integration of the Helmholtz equation over the domain ![]() $\varSigma$, and application of the divergence theorem, we obtain
$\varSigma$, and application of the divergence theorem, we obtain
Consequently, we can formulate the eigenvalue problem
 \begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle (\varDelta +k^2 )\varphi_1=0,\quad \text{in } \varSigma,\\ \displaystyle \dfrac{\partial{\varphi_1}}{\partial{y}}_{|\gamma\cup\gamma_2}=0,\quad \dfrac{\partial{\varphi_1}}{\partial{y}}_{|\gamma_1}=- \dfrac{k^2}{a}\int\nolimits_\varSigma \varphi_1(x,y)\,{\text{d}}\kern0.06em x\,{\text{d}} y,\\ \end{array}\right\}\end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle (\varDelta +k^2 )\varphi_1=0,\quad \text{in } \varSigma,\\ \displaystyle \dfrac{\partial{\varphi_1}}{\partial{y}}_{|\gamma\cup\gamma_2}=0,\quad \dfrac{\partial{\varphi_1}}{\partial{y}}_{|\gamma_1}=- \dfrac{k^2}{a}\int\nolimits_\varSigma \varphi_1(x,y)\,{\text{d}}\kern0.06em x\,{\text{d}} y,\\ \end{array}\right\}\end{equation}
whose eigenvalues belong to the set ![]() $ka=2n{\rm \pi}$, where
$ka=2n{\rm \pi}$, where ![]() $n$ is an integer satisfying
$n$ is an integer satisfying ![]() $n< d/(2a)$, to satisfy
$n< d/(2a)$, to satisfy ![]() $kd<{\rm \pi}$ (this condition ensures the presence of a single propagating mode in the guide).
$kd<{\rm \pi}$ (this condition ensures the presence of a single propagating mode in the guide).
Next, we expand our investigation to include problem (2.6) with the condition that ![]() $\varphi$ decreases exponentially to 0 when
$\varphi$ decreases exponentially to 0 when ![]() $x\to \pm \infty$. By integrating the Helmholtz equation over
$x\to \pm \infty$. By integrating the Helmholtz equation over ![]() $\varSigma$, and considering the boundary condition over
$\varSigma$, and considering the boundary condition over ![]() $\gamma$,
$\gamma$, ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$, along with the condition when
$\gamma _2$, along with the condition when ![]() $x\to \pm \infty$, we obtain
$x\to \pm \infty$, we obtain
Furthermore, by multiplying the Helmholtz equation by ![]() $x$ and integrating over
$x$ and integrating over ![]() $\varSigma$, we obtain
$\varSigma$, we obtain
By combining (B3) and (B4), we formulate an eigenvalue problem defined by
 \begin{equation} \left.\begin{array}{@{}c@{}} (\varDelta +k^2)\,\varphi(x,y),\quad \text{in } \varSigma,\\ \displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma}=0,\\ \displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma_1}=-\dfrac{k^2}{2a}\int_\varSigma \varphi(x,y)\left(1-\dfrac{2x}{e}\right){\text{d}}\kern0.06em x\,{\text{d}} y, \\ \displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma_2}=-\dfrac{k^2}{2a}\int_\varSigma \varphi(x,y)\left(1+\dfrac{2x}{e}\right){\text{d}}\kern0.06em x\,{\text{d}} y, \end{array}\right\}\end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} (\varDelta +k^2)\,\varphi(x,y),\quad \text{in } \varSigma,\\ \displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma}=0,\\ \displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma_1}=-\dfrac{k^2}{2a}\int_\varSigma \varphi(x,y)\left(1-\dfrac{2x}{e}\right){\text{d}}\kern0.06em x\,{\text{d}} y, \\ \displaystyle \dfrac{\partial{\varphi}}{\partial{y}}_{|\gamma_2}=-\dfrac{k^2}{2a}\int_\varSigma \varphi(x,y)\left(1+\dfrac{2x}{e}\right){\text{d}}\kern0.06em x\,{\text{d}} y, \end{array}\right\}\end{equation}
with ![]() $\varphi$ decreasing exponentially to 0 when
$\varphi$ decreasing exponentially to 0 when ![]() $x\to \pm \infty$. Solving (B5) yields eigenvalues
$x\to \pm \infty$. Solving (B5) yields eigenvalues ![]() $ke=n{\rm \pi}$ (while ensuring
$ke=n{\rm \pi}$ (while ensuring ![]() $kd<{\rm \pi}$), with symmetric eigenmodes when
$kd<{\rm \pi}$), with symmetric eigenmodes when ![]() $n$ is odd (and
$n$ is odd (and ![]() $u_1-u_2=0$ from (B4)), and antisymmetric eigenmodes when
$u_1-u_2=0$ from (B4)), and antisymmetric eigenmodes when ![]() $n$ is even (and
$n$ is even (and ![]() $u_1+u_2=0$ from (B3)). Additionally, it provides eigenvalues for
$u_1+u_2=0$ from (B3)). Additionally, it provides eigenvalues for ![]() $ka=2n{\rm \pi}$, associated with eigenmodes that are the superposition of an eigenmode
$ka=2n{\rm \pi}$, associated with eigenmodes that are the superposition of an eigenmode ![]() $\varphi _1$ solution of (B2) and its counterpart
$\varphi _1$ solution of (B2) and its counterpart ![]() $\varphi _2$ when the roles of
$\varphi _2$ when the roles of ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$ are exchanged.
$\gamma _2$ are exchanged.
Figures 9(a,b) depict typical eigenmodes calculated (using Comsol) by solving the eigenvalue problem (B5) in the geometry corresponding to the results in figures 4(a,b), wherein the first two eigenvalues are obtained numerically for ![]() $ke\simeq {\rm \pi}$ and
$ke\simeq {\rm \pi}$ and ![]() $2{\rm \pi}$. Additionally, figure 9(c) presents the first eigenmode for
$2{\rm \pi}$. Additionally, figure 9(c) presents the first eigenmode for ![]() $ka\simeq 2{\rm \pi}$ in the geometry corresponding to the results in figures 4(c,d). In these scenarios, perfect absorptions (
$ka\simeq 2{\rm \pi}$ in the geometry corresponding to the results in figures 4(c,d). In these scenarios, perfect absorptions (![]() $\varphi ^{-}=\varphi ^+_0=0$) were achieved for
$\varphi ^{-}=\varphi ^+_0=0$) were achieved for ![]() $\varphi _{inc}=0$, as the boundary conditions imposed by the sources coincide with those satisfied by an eigenmode.
$\varphi _{inc}=0$, as the boundary conditions imposed by the sources coincide with those satisfied by an eigenmode.

Figure 9. (a,b) Eigenmodes for ![]() $e/d=2$ and
$e/d=2$ and ![]() $a/d=0.5$ associated with the first two eigenvalues
$a/d=0.5$ associated with the first two eigenvalues ![]() $k^2$ of (B5) found numerically at
$k^2$ of (B5) found numerically at ![]() $(kd)^2=2.47$ and 9.86, hence
$(kd)^2=2.47$ and 9.86, hence ![]() $ke= {\rm \pi}$ and
$ke= {\rm \pi}$ and ![]() $2{\rm \pi}$. (c) Eigenmode for
$2{\rm \pi}$. (c) Eigenmode for ![]() $e/d=5$ and
$e/d=5$ and ![]() $a/d=4$ associated with the first eigenvalue
$a/d=4$ associated with the first eigenvalue ![]() $k^2$ of (B2) found numerically at
$k^2$ of (B2) found numerically at ![]() $(kd)^2=2.47$, hence
$(kd)^2=2.47$, hence ![]() $ka= 2{\rm \pi}$.
$ka= 2{\rm \pi}$.