Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-04T19:47:49.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Passive boundary layer control of oblique disturbances by finite-amplitude streaks

Published online by Cambridge University Press:  14 May 2014

Shahab Shahinfar ,
Sohrab S. Sattarzadeh Open the ORCID record for Sohrab S. Sattarzadeh [Opens in a new window]  and
Jens H. M. Fransson
Shahab Shahinfar
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-10044 Stockholm, Sweden
Sohrab S. Sattarzadeh
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-10044 Stockholm, Sweden
Jens H. M. Fransson*
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-10044 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent experimental results on the attenuation of two-dimensional Tollmien–Schlichting wave (TSW) disturbances by means of passive miniature vortex generators (MVGs) have shed new light on the possibility of delaying transition to turbulence and hence accomplishing skin-friction drag reduction. A recurrent concern has been whether this passive flow control strategy would work for other types of disturbances than plane TSWs in an experimental configuration where the incoming disturbance is allowed to fully interact with the MVG array. In the present experimental investigation we show that not only TSW disturbances are attenuated, but also three-dimensional single oblique wave (SOW) and pair of oblique waves (POW) disturbances are quenched in the presence of MVGs, and that transition delay can be obtained successfully. For the SOW disturbance an unusual interaction between the wave and the MVGs occurs, leading to a split of the wave with one part travelling with a ‘mirrored’ phase angle with respect to the spanwise direction on one side of the MVG centreline. 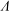This gives rise to $\Lambda $-vortices on the centreline, which force a low-speed streak on the centreline, strong enough to overcome the high-speed streak generated by the MVGs themselves. Both these streaky boundary layers seem to act stabilizing on unsteady perturbations. The challenge in a passive control method making use of a non-modal type of disturbances to attenuate modal disturbances lies in generating stable streamwise streaks which do not themselves break down to turbulence.

JFM classification

Boundary Layers: Boundary layer control Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 749 , 25 June 2014 , pp. 1 - 36
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bake, S., Fernholz, H. H. & Kachanov, Y. S. 2000 Resemblence of K- and N-regimes of boundary-layer transition at late stages. Eur. J. Mech. (B/ Fluids) 19, 1–22.Google Scholar
Berlin, S., Lundbladh, A. & Henningson, D. S. 1994 Spatial simulations of oblique transition in a boundary layer. Phys. Fluids 6, 1949–1951.Google Scholar
Berlin, S., Wiegel, M. & Henningson, D. S. 1999 Numerical and experimental investigations of oblique boundary layer transition. J. Fluid Mech. 393, 23–57.Google Scholar
Boiko, A. V., Westin, K. J. A., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subjected to free stream turbulence. Part 2. The role of TS-waves in the transition process. J. Fluid Mech. 281, 219–245.Google Scholar
Camarri, S., Fransson, J. H. M. & Talamelli, A. 2013 Numerical investigation of the AFRODITE transition control strategy. In Progress in Turbulence V, pp. 65–69. Springer.Google Scholar
Corke, T. C., BarSever, A. & Morkovin, M. V. 1986 Experiments on transition enhancement by distributed roughness. Phys. Fluids 29, 3199–3213.Google Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14, L57–L60.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien–Schlichting-like waves in streaky boundary layers. Eur. J. Mech. (B/Fluids) 23, 815–833.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.Google Scholar
Elofsson, P. A. & Alfredsson, P. H. 2000 An experimental study of oblique transition in a Blasius boundary layer flow. Eur. J. Mech. (B/Fluids) 19, 615–636.CrossRefGoogle Scholar
Fransson, J. H. M. 2010 Turbulent spot evolution in spatially invariant boundary layers. Phys. Rev. E 81, 035301(R).Google Scholar
Fransson, J. H. M. & Alfredsson, P. H. 2003 On the disturbance growth in an asymptotic suction boundary layer. J. Fluid Mech. 482, 51–90.Google Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2004 Experimental and theoretical investigation of the nonmodal growth of steady streaks in a flat plate boundary layer. Phys. Fluids 16 (10), 3627–3638.Google Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilisation of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110.Google Scholar
Fransson, J. H. M., Fallenius, B. E. G., Shahinfar, S., Sattarzadeh, S. S. & Talamelli, A. 2011 Advanced fluid research on drag reduction in turbulence experiments afrodite. J. Phys.: Conf. Ser. 318, 032007.Google Scholar
Fransson, J. H. M. & Talamelli, A. 2012 On the generation of steady streamwise streaks in flat-plate boundary layers. J. Fluid Mech. 698, 211–234.CrossRefGoogle Scholar
Fransson, J. H. M., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96, 064501.Google Scholar
Gaponenko, V. & Kachanov, Y.1994 New methods of generation of controlled spectrum instability waves in boundary layers. In ICMAR, Part 1, Inst. Theor. and Appl. Mech., Novosibirsk pp. 125–130.Google Scholar
Herbert, Th. 1988 Secondary instability of boundary-layers. Annu. Rev. Fluid Mech. 20, 487–526.Google Scholar
Hultgren, L. S. & Gustavsson, L. H. 1981 Algebraic growth of disturbances in a laminar boundary layer. Phys. Fluids 24 (6), 1000–1004.CrossRefGoogle Scholar
Johansson, A. V. & Alfredsson, P. H. 1982 On the structure of turbulent channel flow. J. Fluid Mech. 122, 295–314.Google Scholar
Kachanov, Y. S. 1994 Physical mechanism of laminar boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–482.CrossRefGoogle Scholar
Kachanov, Y. S. & Tararykin, O. I. 1987 Experimental investigation of a relaxating boundary layer. Izv. SO AN SSSR, Ser. Tech. Nauk 18 (5), 9–19.Google Scholar
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. 1962 The three-dimensional nature of boundary layer instability. J. Fluid Mech. 12, 1–34.Google Scholar
Klingmann, B. G. B., Boiko, A., Westin, K. J. A., Kozlov, V. V. & Alfredsson, P. H. 1993 Experiments on the stability of Tollmien–Schlichting waves. Eur. J. Mech. (B/ Fluids) 12, 493–514.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.Google Scholar
Lindgren, B. & Johansson, A. V.2002 Evaluation of the flow quality in the mtl wind-tunnel. Tech. Rep. KTH/MEK/TR-02/13-SE. KTH Mechanics, Stockholm.Google Scholar
Morkovin, M. V. 1969 The many faces of transition. In Viscous Drag Reduction (ed. Wells, C. S.), Plenum.Google Scholar
Pearcey, H. H. 1961 Shock-induced separation and its prevention. In Boundary Layer and Flow Control, its Principle and Applications (ed. Lachmann, G. V.), Pergamon.Google Scholar
Radeztsky, R. H. Jr., Reibert, M. S. & Saric, W. S. 1999 Effect of isolated micron-sized roughness on transition in swept-wing flows. AIAA J. 37 (11), 1370–1377.CrossRefGoogle Scholar
Saric, W. S., Carrillo, R. B. Jr. & Reibert, M. S. 1998 Leading-edge roughness as a transition control mechanism. AIAA Paper 98-0781.Google Scholar
Saric, W. S. & Reed, H. L.2002 Supersonic laminar flow control on swept wings using distributed roughness. AIAA Paper 02-0147.Google Scholar
Schlatter, P., Deusebio, E., de Lange, R. & Brandt, L. 2010 Numerical study of the stabilisation of boundary-layer disturbances by finite amplitude streaks. Intl J. Flow Control 2, 259–288.Google Scholar
Schlichting, H. 1933 Berechnung der anfachung kleiner störungen bei der plattenströmung. Z. Angew. Math. Mech. 13, 171–174.Google Scholar
Schlichting, H. 1979 Boundary Layer Theory. McGraw-Hill.Google Scholar
Schmid, P. J. & Henningson, D. S. 1992 A new mechanism for rapid transition involving a pair of oblique waves. Phys. Fluids A 4, 1986–1989.Google Scholar
Schubauer, G. B. & Skramstad, H. K. 1947 Laminar boundary layer oscillations and the stability of laminar flow. J. Aero. Sci. 14, 69–78.Google Scholar
Shahinfar, S., Fransson, J. H. M., Sattarzadeh, S. S. & Talamelli, A. 2013 On the scaling of streamwise boundary layer streaks and their ability to reduce skin-friction drag. J. Fluid Mech. 733, 1–32.Google Scholar
Shahinfar, S., Sattarzadeh, S. S., Fransson, J. H. M. & Talamelli, A. 2012 Revival of classical vortex generators now for transition delay. Phys. Rev. Lett. 109, 074501.CrossRefGoogle ScholarPubMed
Tollmien, W.1929 Über die entstehung der turbulenz. Nachr. Ges. Wiss. Göttingen 21–24, English translation NACA TM 609, 1931.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
White, E. B. & Saric, W. S.2000 Application of variable leading-edge roughness for transition control on swept wings. AIAA Paper 2000-0283.Google Scholar