Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T07:03:11.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory sensitivity patterns for global modes in wakes

Published online by Cambridge University Press:  18 May 2012

Outi Tammisola
Outi Tammisola*
Affiliation:
Linné Flow Centre, KTH Mechanics, Royal Institute of Technology, S-100 44 Stockholm, Sweden
*
†Present address: Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Globally unstable wakes with co-flow at intermediate Reynolds numbers are studied, to quantify important spatial regions for the development and control of the global instability. One region of high structural sensitivity is found close to the inlet for all wakes, in agreement with previous findings for cylinder wakes. A second, elongated region of high structural sensitivity is seen downstream of the first one for unconfined wakes at 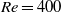. When base-flow modifications are considered, a spatially oscillating sensitivity pattern is found inside the downstream high-structural-sensitivity region. This implies that the same change in the base flow can either destabilize or stabilize the flow, depending on the exact position where it is applied. It is shown that the sensitivity pattern remains unchanged for different choices of streamwise boundary conditions and numerical resolution. The actual base-flow is modified in selected configurations, and the linear global modes recomputed. It is confirmed that the linear global eigenvalues move according to the predicted sensitivity pattern for small-amplitude base-flow modifications, for which the theory applies. We also look at the implications of a small control cylinder for the flow. Only the upstream high-sensitivity region proves to be robust in terms of control, but one should be careful not to disturb the flow in the downstream high-sensitivity region, in order to achieve control. The findings can have direct implications for the numerical resolution requirements for wakes at higher Reynolds numbers. Furthermore, they provide one more possible explanation for why confined wakes have a more narrow frequency spectrum than unconfined wakes.

JFM classification

Instability: Absolute/convective instability Flow Control: Instability control Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 251 - 277
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Åkervik, E. 2011 Personal communication.Google Scholar
2. Åkervik, E., Hœpffner, J., Ehrenstein, U. & Henningson, D. S. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global eigenmodes. J. Fluid Mech. 579, 305–314.CrossRefGoogle Scholar
3. Bearman, P. W. & Zdravkovich, M. M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89, 33–47.CrossRefGoogle Scholar
4. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
5. Fey, U., König, M. & Eckelmann, H. 1998 A new Strouhal–Reynolds-number relationship for the circular cylinder in the range . Phys. Fluids 10 (7), 1–3.CrossRefGoogle Scholar
6. Filon, L. N. G. 1926 The forces on a cylinder in a stream of viscous fluid. Proc. R. Soc. Lond. A 113, 7–27.Google Scholar
7. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
8. Hill, D. 1992 A theoretical approach for analyzing the restabilization of wakes. AIAA Paper 92–0067.Google Scholar
9. Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
10. Hussain, A. K. M. F. & Zaman, Q. 1978 The free shear layer tone phenomenon and probe interference. J. Fluid Mech. 87 (2), 349–383.CrossRefGoogle Scholar
11. Imai, I. 1951 On the asymptotic behaviour of viscous fluid flow at a great distance from a cylindrical body, with special reference to Filon’s paradox. Proc. R. Soc. Lond. A 208, 487–516.Google Scholar
12. Juniper, M. P. 2006 The effect of confinement on the stability of two-dimensional shear flows. J. Fluid Mech. 565, 171–195.CrossRefGoogle Scholar
13. Juniper, M., Tammisola, O. & Lundell, F. 2011 The local and global stability of confined planar wakes at intermediate Reynolds number. J. Fluid Mech. 686, 218–238.CrossRefGoogle Scholar
14. Kovasznay, L. 1949 Hot-wire investigation of the wake behind cylinders at low Reynolds numbers. Proc. R. Soc. Lond. A 198 (1053), 174–190.Google Scholar
15. Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
16. Pralits, J., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
17. Rees, S. J. & Juniper, M. P. 2010 The effect of confinement on the stability of viscous planar jets and wakes. J. Fluid Mech. 656, 309–336.CrossRefGoogle Scholar
18. Richter, A. & Naudascher, E. 1976 Fluctuating forces on a rigid circular cylinder in confined flow. J. Fluid Mech. 78, 561–576.CrossRefGoogle Scholar
19. Rowley, C. W., Colonius, T. & Basu, A. J. 2002 On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities. J. Fluid Mech. 455, 315–346.CrossRefGoogle Scholar
20. Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
21. Tammisola, O., Lundell, F., Schlatter, P., Wehrfritz, A. & Söderberg, L. D. 2011 Global linear and nonlinear stability of viscous confined plane wakes with co-flow. J. Fluid Mech. 675, 397–434.CrossRefGoogle Scholar
22. Unal, M. F. & Rockwell, D. 1987 On vortex formation from a cylinder. Part 2. Control by splitter-plate interference. J. Fluid Mech. 190, 513–529.CrossRefGoogle Scholar
23. Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
24. Zdravkovich, M. M. 1997 Flow Around Circular Cylinders, vol. 1. Oxford University Press.CrossRefGoogle Scholar
25. Zebib, A. 1987 Stability of viscous flow past a circular cylinder. J. Engng Maths 21 (2), 155–165.CrossRefGoogle Scholar