Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T23:12:01.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal perturbation growth in axisymmetric intrusions

Published online by Cambridge University Press:  14 December 2016

Bruce R. Sutherland  and
C. P. Caulfield
Bruce R. Sutherland*
Affiliation:
Departments of Physics and of Earth and Atmospheric Sciences, University of Alberta, Edmonton, AB, Canada  T6G 2E1
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The cylindrical lock-release laboratory experiments of Sutherland & Nault (J. Fluid Mech., vol. 586, 2007, pp. 109–118) showed that a radially advancing symmetric intrusive gravity current spreads not as an expanding annulus (as is the case for bottom-propagating gravity currents), but rather predominantly along azimuthally periodic radial ‘spokes’. Here, we investigate whether the spokes are associated with azimuthal perturbations that undergo ‘optimal’ growth. We use a nonlinear axisymmetric numerical simulation initialised with the experimental parameters to compute the time-evolving axisymmetric base state of the collapsing lock fluid. Using fields from this rapidly evolving base state together with the linearised perturbation equations and their adjoint, the ‘direct–adjoint looping’ method is employed to identify, as a function of the azimuthal wavenumber 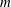$m$, the vertical–radial structure of the set of initial perturbations that exhibit the largest total perturbation energy gain over a target time 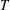$T$. Of this set of perturbations, the one that extracts energy fastest, and so is expected to be observed to emerge first from the base flow, has azimuthal wavenumber comparable to the number of spokes observed in the experiment.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Instability: Instability
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 811 , 25 January 2017 , R4
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, C., Caulfield, C. P. & Chomaz, J.-M. 2013 Transient perturbation growth in time-dependent mixing layers. J. Fluid Mech. 717, 90–133.CrossRefGoogle Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.CrossRefGoogle Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: nonnormality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities of spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Kaminski, A. K., Caulfield, C. P. & Taylor, J. R. 2014 Transient growth in strongly stratified shear layers. J. Fluid Mech. 758, R4.CrossRefGoogle Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimization approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77, 085901.CrossRefGoogle ScholarPubMed
Klaassen, G. P. & Peltier, W. R. 1991 The influence of stratification on secondary instability in free shear layers. J. Fluid Mech. 227, 71–106.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.CrossRefGoogle Scholar
McMillan, J. M. & Sutherland, B. R. 2010 The lifecycle of axisymmetric internal solitary waves. Nonlinear Process. Geophys. 17, 443–453.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Simpson, J. E. 1972 Effects of lower boundary on the head of a gravity current. J. Fluid Mech. 53, 759–768.CrossRefGoogle Scholar
Sutherland, B. R. & Nault, J. T. 2007 Intrusive gravity currents propagating along thin and thick interfaces. J. Fluid Mech. 586, 109–118.CrossRefGoogle Scholar