Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-21T00:03:12.879Z Has data issue: false hasContentIssue false
  • English
  • Français

On velocity and reactive scalar spectra in turbulent premixed flames

Published online by Cambridge University Press:  07 August 2014

H. Kolla ,
E. R. Hawkes ,
A. R. Kerstein ,
N. Swaminathan  and
J. H. Chen
H. Kolla*
Affiliation:
Combustion Research Facility, Sandia National Laboratories, Livermore, CA 94550, USA
E. R. Hawkes
Affiliation:
School of Mechanical and Manufacturing Engineering, The University of New South Wales, Sydney, Australia
A. R. Kerstein
Affiliation:
72 Lomitas Road, Danville, CA 94526, USA
N. Swaminathan
Affiliation:
Engineering Department, University of Cambridge, Cambridge CB2 1PZ, UK
J. H. Chen
Affiliation:
Combustion Research Facility, Sandia National Laboratories, Livermore, CA 94550, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kinetic energy and reactive scalar spectra in turbulent premixed flames are studied from compressible three-dimensional direct numerical simulations (DNS) of a temporally evolving rectangular slot-jet premixed flame, a statistically one-dimensional configuration. The flames correspond to a lean premixed hydrogen–air mixture at an equivalence ratio of 0.7, preheated to 700 K and at 1 atm, and three DNS are considered with a fixed jet Reynolds number of 10 000 and a jet Damköhler number varying between 0.13 and 0.54. For the study of spectra, motivated by the need to account for density change, which can be locally strong in premixed flames, a new density-weighted definition for two-point velocity/scalar correlations is proposed. The density-weighted two-point correlation tensor retains the essential properties of its constant-density (incompressible) counterpart and recovers the density-weighted Reynolds stress tensor in the limit of zero separation. The density weighting also allows the derivation of balance equations for velocity and scalar spectrum functions in the wavenumber space that illuminate physics unique to combusting flows. Pressure–dilatation correlation is a source of kinetic energy at high wavenumbers and, analogously, reaction rate–scalar fluctuation correlation is a high-wavenumber source of scalar energy. These results are verified by the spectra constructed from the DNS data. The kinetic energy spectra show a distinct inertial range with a 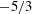$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}-5/3$ scaling followed by a ‘diffusive–reactive’ range at higher wavenumbers. The exponential drop-off in this range shows a distinct inflection in the vicinity of the wavenumber corresponding to a laminar flame thickness, 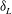$\delta _L$, and this is attributed to the contribution from the pressure–dilatation term in the energy balance in wavenumber space. Likewise, a clear spike in spectra of major reactant species (hydrogen) arising from the reaction-rate term is observed at wavenumbers close to 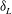$\delta _L$. It appears that in the inertial range classical scaling laws for the spectra involving the Kolmogorov scale are applicable, but in the high-wavenumber range where chemical reactions have a strong signature the laminar flame thickness produces a better collapse. It is suggested that a full scaling should perhaps involve the Kolmogorov scale, laminar flame thickness, Damköhler number and Karlovitz number.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Reacting Flows: Turbulent reacting flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 456 - 487
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of small conductivity. J. Fluid Mech. 5, 134–139.Google Scholar
Bilger, R. W. 2004 Some aspects of scalar dissipation. Flow Turbul. Combust. 72, 93–114.Google Scholar
Bilger, R. W., Saetran, L. R. & Krishnamoorthy, L. V. 1991 Reaction in a scalar mixing layer. J. Fluid Mech. 233, 211–242.CrossRefGoogle Scholar
Chakraborty, N. & Swaminathan, N. 2007 Influence of the Damköhler number on turbulence–scalar interaction in premixed flames. I. Physical insight. Phys. Fluids 19, 045103.Google Scholar
Chen, J. H., Choudhary, A., de Supinski, B., DeVries, M., Hawkes, E. R., Klasky, S., Liao, W. K., Ma, K. L., Mellor-Crummey, J., Podhorski, N., Sankaran, R., Shende, S. & Yoo, C. S. 2009 Terascale direct numerical simulations of turbulent combustion using S3D. Comput. Sci. Disc. 2, 1–31.Google Scholar
Corrsin, S. 1961 The reactant concentration spectrum in turbulent mixing with a first order reaction. J. Fluid Mech. 11, 407–416.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Furukawa, J., Noguchi, Y., Hirano, T. & Williams, F. A. 2002 Anisotropic enhancement of turbulence in large-scale, low-intensity turbulent premixed propane–air flames. J. Fluid Mech. 462, 209–243.Google Scholar
Guttenfelder, W. A., King, G. B., Gore, J. P., Laurendeau, N. M. & Renfro, M. W. 2003 Hydroxyl time-series measurements and simulations for turbulent premixed jet flames in the thickened preheat regime. Combust. Flame 135, 381–403.CrossRefGoogle Scholar
Hawkes, E. R., Chatakonda, O., Kolla, H., Kerstein, A. R. & Chen, J. H. 2012 A petascale direct numerical simulation study of the modelling of flame wrinkling for large-eddy simulations in intense turbulence. Combust. Flame 159 (8), 2690–2703.Google Scholar
Hinze, J. O. 1975 Turbulence, 2nd edn. McGraw-Hill.Google Scholar
Jones, W. P. 1993 Turbulence modelling and numerical solution methods for variable density and combusting flows. In Turbulent Reacting Flows (ed. Libby, P. A. & Williams, F. A.), pp. 309–374. Academic Press.Google Scholar
Kariuki, J., Dawson, J. R. & Mastorakos, E. 2012 Measurements in turbulent premixed bluff body flames close to blow-off. Combust. Flame 159, 2589–2607.Google Scholar
Kee, R. J., Dixon-Lewis, G., Warnatz, J., Coltrin, M. E. & Miller, J. A.1986 A Fortran computer code package for the evaluation of gas-phase multicomponent transport properties. Tech. Rep. SAND86-8246. Sandia National Laboratories.Google Scholar
Kee, R. J., Rupley, F. M., Meeks, E. & Miller, J. A.1996 CHEMKIN-III: a Fortran chemical kinetics package for the analysis of gas-phase chemical and plasma kinetics. Tech. Rep. SAND96-8216. Sandia National Laboratories.Google Scholar
Kennedy, C. A. & Carpenter, M. H. 1994 Several new numerical methods for compressible shear-layer simulations. Appl. Numer. Maths 14 (4), 397–433.Google Scholar
Kennedy, C. A., Carpenter, M. H. & Lewis, R. M. 2000 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Maths 35 (3), 177–219.Google Scholar
Knaus, R. & Pantano, C. 2009 On the effect of heat release in turbulence spectra of non-premixed reacting shear layers. J. Fluid Mech. 626, 67–109.CrossRefGoogle Scholar
Kosály, G. 1993 Frequency spectra of reactant fluctuations in turbulent flows. J. Fluid Mech. 246, 489–502.Google Scholar
Krzywoblocki, M. Z. E. 1952 On the invariants in the turbulence in compressible viscous fluids. J. Franklin Inst. 254, 317–322.Google Scholar
Li, J., Zhao, Z., Kazarov, A. & Dryer, F. L. 2004 An updated comprehensive kinetic model of hydrogen combustion. Intl J. Chem. Kinet. 36, 566–575.Google Scholar
Passot, T. & Pouquet, A. 1987 Numerical simulation of compressible homogeneous flows in the turbulent regime. J. Fluid Mech. 181, 441–466.Google Scholar
Poinsot, T. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flow. J. Comput. Phys. 101, 104–129.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA Tech. Memo. 81315. NASA Ames Research Center, Stanford, CA.Google Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence journal. J. Fluid Mech. 227, 473–493.Google Scholar
Swaminathan, N. & Grout, R. W. 2006 Interaction of turbulence and scalar fields in premixed flames. Phys. Fluids 18, 045102.Google Scholar
Ulitsky, M. & Collins, L. 1997 Application of the eddy damped quasi-normal Markovian spectral transport theory to premixed turbulent flames. Phys. Fluids 9, 3410–3430.Google Scholar
Vaishnavi, P., Kronenburg, A. & Pantano, C. 2008 On the spatial length scales of scalar dissipation in turbulent jet flames. J. Fluid Mech. 596, 103–132.Google Scholar
Wang, G., Karpetis, A. N. & Barlow, R. S. 2007 Dissipation length scales in turbulent nonpremixed jet flames. Combust. Flame 148, 62–75.CrossRefGoogle Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
Xia, Y., Liu, Y., Vaithianathan, T. & Collins, L. R. 2010 Eddy damped quasinormal Markovian theory for chemically reactive scalars in isotropic turbulence. Phys. Fluids 22, 045103.Google Scholar
Yeung, P. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.Google Scholar
Yoo, C. S. & Im, H. G. 2007 Characteristic boundary conditions for simulations of compressible reacting flows with multi-dimensional, viscous and reaction effects. Combust. Theor. Model. 11, 259–286.Google Scholar
Yoshizawa, A., Matsuo, Y. & Mizobuchi, Y. 2013 A construction of the Reynolds-averaged turbulence transport equations in a variable-density flow, based on the concept of mass-weighted fluctuations. Phys. Fluids 25, 075105.Google Scholar
Zeman, O. 1991 On the decay of compressible isotropic turbulence. Phys. Fluids A 3, 951–955.Google Scholar
Zhang, S. & Rutland, C. J. 1995 Premixed flame effects on turbulence and pressure-related terms. Combust. Flame 102, 447–461.Google Scholar