Article contents
On the thermal equilibrium state of large-scale flows
Published online by Cambridge University Press: 13 June 2019
Abstract
In a forced three-dimensional turbulent flow the scales larger than the forcing scale have been conjectured to reach a thermal equilibrium state forming a 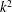 $k^{2}$ energy spectrum, where
$k^{2}$ energy spectrum, where 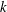 $k$ is the wavenumber. In this work we examine the properties of these large scales in turbulent flows with the use of numerical simulations. We show that the choice of forcing can strongly affect the behaviour of the large scales. A spectrally dense forcing (a forcing that acts on all modes inside a finite-width spherical shell) with long correlation times may lead to strong deviations from the
$k$ is the wavenumber. In this work we examine the properties of these large scales in turbulent flows with the use of numerical simulations. We show that the choice of forcing can strongly affect the behaviour of the large scales. A spectrally dense forcing (a forcing that acts on all modes inside a finite-width spherical shell) with long correlation times may lead to strong deviations from the 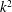 $k^{2}$ energy spectrum, while a spectrally sparse forcing (a forcing that acts only on a few modes) with short correlated time scale can reproduce the thermal spectrum. The origin of these deviations is analysed and the involved mechanisms is unravelled by examining: (i) the number of triadic interactions taking place, (ii) the spectrum of the nonlinear term, (iii) the amplitude of interactions and the fluxes due to different scales and (iv) the transfer function between different shells of wavenumbers. It is shown that the spectrally dense forcing allows for numerous triadic interactions that couple one large-scale mode with two forced modes and this leads to an excess of energy input at the large scales. This excess of energy is then moved back to the small scales by self-interactions of the large-scale modes and by interactions with the turbulent small scales. The overall picture that arises from the present analysis is that the large scales in a turbulent flow resemble a reservoir that is in (non-local) contact with a second out-of-equilibrium reservoir consisting of the smaller (forced, turbulent and dissipative) scales. If the injection of energy at the large scales from the forced modes is relative weak (as is the case for the spectrally sparse forcing) then the large-scale spectrum remains close to a thermal equilibrium and the role of long-range interactions is to set the global energy (temperature) of the equilibrium state. If, on the other hand, the long-range interactions are dominant (as is the case for the spectrally dense forcing), the large-scale self-interactions cannot respond fast enough to bring the system into equilibrium. Then the large scales deviate from the equilibrium state with energy spectrum that may display exponents different from the
$k^{2}$ energy spectrum, while a spectrally sparse forcing (a forcing that acts only on a few modes) with short correlated time scale can reproduce the thermal spectrum. The origin of these deviations is analysed and the involved mechanisms is unravelled by examining: (i) the number of triadic interactions taking place, (ii) the spectrum of the nonlinear term, (iii) the amplitude of interactions and the fluxes due to different scales and (iv) the transfer function between different shells of wavenumbers. It is shown that the spectrally dense forcing allows for numerous triadic interactions that couple one large-scale mode with two forced modes and this leads to an excess of energy input at the large scales. This excess of energy is then moved back to the small scales by self-interactions of the large-scale modes and by interactions with the turbulent small scales. The overall picture that arises from the present analysis is that the large scales in a turbulent flow resemble a reservoir that is in (non-local) contact with a second out-of-equilibrium reservoir consisting of the smaller (forced, turbulent and dissipative) scales. If the injection of energy at the large scales from the forced modes is relative weak (as is the case for the spectrally sparse forcing) then the large-scale spectrum remains close to a thermal equilibrium and the role of long-range interactions is to set the global energy (temperature) of the equilibrium state. If, on the other hand, the long-range interactions are dominant (as is the case for the spectrally dense forcing), the large-scale self-interactions cannot respond fast enough to bring the system into equilibrium. Then the large scales deviate from the equilibrium state with energy spectrum that may display exponents different from the 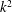 $k^{2}$ spectrum.
$k^{2}$ spectrum.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 23
- Cited by


