Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T09:33:49.191Z Has data issue: false hasContentIssue false
  • English
  • Français

On the theory of a shock wave driven by a corrugated piston in a non-ideal fluid

Published online by Cambridge University Press:  05 December 2011

J. W. Bates
J. W. Bates*
Affiliation:
Plasma Physics Division, U.S. Naval Research Laboratory, Washington, DC 20375, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the context of an Eulerian fluid description, we investigate the dynamics of a shock wave that is driven by the steady impulsively initiated motion of a two-dimensional planar piston with small corrugations superimposed on its surface. This problem was originally solved by Freeman (Proc. Royal Soc. A, vol. 228, 1955, pp. 341–362), who showed that piston-driven shocks are unconditionally stable when the fluid medium through which they propagate is an ideal gas. Here, we generalize Freeman’s mathematical framework to account for a fluid characterized by an arbitrary equation of state. We find that a sufficient condition for shock stability is , where 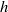is the D’yakov parameter and 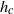is a critical value less than unity. For values of 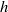within this range, linear perturbations imparted to the front by the piston at time 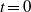attenuate asymptotically as 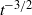. Outside of this range, the temporal behaviour of perturbations is more difficult to determine and further analysis is required to assess the stability of a shock front under such circumstances. As a benchmark of the main conclusions of this paper, we compare our generalized expression for the linearized shock-ripple amplitude with an independent Bessel-series solution derived by Zaidel’ (J. Appl. Math. Mech., vol. 24, 1960, pp. 316–327) and find excellent agreement.

JFM classification

Instability: Absolute/convective instability Mathematical Foundations: General fluid mechanics Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 146 - 164
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bates, J. W. 2004 Initial-value-problem solution for isolated rippled shock fronts in arbitrary fluid media. Phys. Rev. E 69, 056313.CrossRefGoogle ScholarPubMed
2. Bates, J. W. 2007 Instability of isolated planar shock waves. Phys. Fluids 19, 094102.CrossRefGoogle Scholar
3. Bates, J. W. & Montgomery, D. C. 1999 Some numerical studies of exotic shock wave behaviour. Phys. Fluids 11, 462–475.CrossRefGoogle Scholar
4. Bates, J. W. & Montgomery, D. C. 2000 The D’yakov–Kontorovich instability of shock waves in real gases. Phys. Rev. Lett. 84, 1180–1183.CrossRefGoogle ScholarPubMed
5. Bethe, H. A. 1942The theory of shock waves for an arbitrary equation of state. Clearinghouse for Federal Scientific and Technical Information, US Department of Commerce, Washington, DC, Report No. PB-32189 (unpublished).Google Scholar
6. Blackburn, D. 1953Unsteady perturbations of strong shock waves. Ph.D. Thesis, Manchester University.Google Scholar
7. Briscoe, M. G. & Kovitz, A. A. 1968 Experimental and theoretical study of the stability of plane shock waves reflected normally from perturbed flat walls. J. Fluid Mech. 31, 529–546.CrossRefGoogle Scholar
8. Busemann, A. 1943 Infinitesimale kegelige Überschallströmung. Schriften der Deutschen Akademie für Luftfahrtforschung 7B, 105–122.Google Scholar
9. Courant, R. & Friedrichs, K. O. 1957 Supersonic Flow and Shock Waves. Wiley.Google Scholar
10. Duderstadt, J. J. & Moses, G. A. 1982 Inertial Confinement Fusion. Wiley.Google Scholar
11. Duvall, G. P. & Graham, R. A. 1977 Phase transitions under shock-wave loading. Rev. Mod. Phys. 49, 523–579.CrossRefGoogle Scholar
12. D’yakov, S. P. 1954 On the stability of shock waves. Zh. Eksp. Teor. Fiz. 27, 288–296.Google Scholar
13. Eliezer, S. 2002 The Interaction of High-Power Lasers with Plasmas. IOP Publishing.CrossRefGoogle Scholar
14. Eliezer, S., Ghatak, A. & Hora, H. 2002 Fundamentals of Equation of State. World Scientific.CrossRefGoogle Scholar
15. Erpenbeck, J. J. 1962 Stability of step shocks. Phys. Fluids 5, 1181–1187.CrossRefGoogle Scholar
16. Fowles, G. R. 1976 Conditional stability of shock waves – a criterion for detonation. Phys. Fluids 19, 227–238.CrossRefGoogle Scholar
17. Fowles, G. R. 1981 Stimulated and spontaneous emission of acoustic waves from shock fronts. Phys. Fluids 24, 220–227.CrossRefGoogle Scholar
18. Fowles, G. R. & Swan, G. W. 1973 Stability of plane shock waves. Phys. Rev. Lett. 30, 1023–1025.CrossRefGoogle Scholar
19. Freeman, N. C. 1955 A theory of the stability of plane shock waves. Proc. R. Soc. Lond. A 228, 341–362.Google Scholar
20. Freeman, N. C. 1957 On the stability of plane shock waves. J. Fluid Mech. 2, 397–411.CrossRefGoogle Scholar
21. Gardner, C. 1963 Comments on Stability of step shocks. Phys. Fluids 6, 1366–1367.CrossRefGoogle Scholar
22. Gradshteyn, I. S. & Ryzhik, I. M. 1994 Table of Integrals, Series, and Products. Elsevier/Academic Press.Google Scholar
23. Griffiths, D. J. 1981 Introduction to Electrodynamics. Prentice-Hall.Google Scholar
24. Griffiths, R. W., Sandeman, R. J. & Hornung, H. G. 1975 The stability of shock waves in ionizing and dissociating gases. J. Phys. D: Appl. Phys. 8, 1681–1691.Google Scholar
25. Ishizaki, R. & Nishihara, K. 1997 Propagation of a rippled shock wave driven by nonuniform laser ablation. Phys. Rev. Lett. 78, 1920–1923.CrossRefGoogle Scholar
26. Ishizaki, R. & Nishihara, K. 1998 Model of hydrodynamic perturbation growth in the start-up phase of laser implosion. Phys. Rev. E 58, 3744–3767.CrossRefGoogle Scholar
27. Kane, J. O., Robey, H. F., Remington, B. A., Drake, R. P., Knauer, J., Ryutov, D. D., Louis, H., Teyssier, R., Hurricane, O., Arnett, D., Rosner, R. & Calder, A. 2001 Interface imprinting by a rippled shock using an intense laser. Phys. Rev. E 63, 055401.CrossRefGoogle ScholarPubMed
28. Kontorovich, V. M. 1957 Concerning the stability of shock waves. Sov. Phys. JETP 6, 1179–1180.Google Scholar
29. Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon Press.Google Scholar
30. Lighthill, M. J. 1949 The diffraction of blast. I. Proc. R. Soc. Lond. A 198, 454–470.Google Scholar
31. Lighthill, M. J. 1950 The diffraction of blast. II. Proc. R. Soc. Lond. A 200, 554–565.Google Scholar
32. Lighthill, M. J. 2003 An Introduction to Fourier Analysis and Generalized Functions. Cambridge University Press.Google Scholar
33. Lindl, J. D. 1998 Inertial Confinement Fusion. Springer.Google Scholar
34. Menikoff, R. & Plohr, B. J. 1989 The Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 61, 75–130.CrossRefGoogle Scholar
35. Nilson, P. M., Mangles, S. P. D., Willingale, L., Kaluza, M. C., Thomas, A. G. R., Tatarakis, M., Najmudin, Z., Clarke, R. J., Lancaster, K. L., Karsch, S., Schreiber, J., Evans, R. G., Dangor, A. E. & Krushelnick, K. 2009 Generation of ultrahigh-velocity ionizing shocks with petawatt-class laser pusles. Phys. Rev. Lett. 103, 255001.CrossRefGoogle Scholar
36. Oberhettinger, F. 1973 Fourier Expansions: A Collection of Formulas. Academic Press.Google Scholar
37. Roberts, A. E. 1945Stability of a steady plane shock. Los Alamos Scientic Laboratory Report No. LA-299 (unpublished).Google Scholar
38. Swan, G. W. & Fowles, G. R. 1975 Shock wave stability. Phys. Fluids 18, 28–35.CrossRefGoogle Scholar
39. Tumin, A. 2008 Comment on Instability of isolated planar shock waves. Phys. Fluids 20, 029101.CrossRefGoogle Scholar
40. Whittaker, E. T. & Watson, G. N. 1965 A Course of Modern Analysis. Cambridge University Press.Google Scholar
41. Wolfram, S. 2003 The Mathematica Book: 5th Edition. Cambridge University Press.Google Scholar
42. Wouchuk, J. G. & Cavada, J. L. 2004 Spontaneous acoustic emission of a corrugated shock wave in the presence of a reflecting surface. Phys. Rev. E 70, 046303.CrossRefGoogle ScholarPubMed
43. Zaidel’, R. M. 1960 Shock waves from a slightly curved piston. J. Appl. Math. Mech. 24, 316–327.CrossRefGoogle Scholar