Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vladimirov, V. A.
2013.
Dumbbell micro-robot driven by flow oscillations.
Journal of Fluid Mechanics,
Vol. 717,
Issue. ,
Felderhof, B. U.
2014.
Swimming of an assembly of rigid spheres at low Reynolds number.
The European Physical Journal E,
Vol. 37,
Issue. 11,
Ishikawa, Takuji
and
Vladimirov, V. A.
2015.
A Stepping Microrobot Controlled by Flow Oscillations.
Journal of Fluids Engineering,
Vol. 137,
Issue. 8,
Felderhof, B. U.
2015.
Efficient swimming of an assembly of rigid spheres at low Reynolds number.
The European Physical Journal E,
Vol. 38,
Issue. 8,
Bet, Bram
Boosten, Gijs
Dijkstra, Marjolein
and
van Roij, René
2017.
Efficient shapes for microswimming: From three-body swimmers to helical flagella.
The Journal of Chemical Physics,
Vol. 146,
Issue. 8,
Box, F.
Han, E.
Tipton, C. R.
and
Mullin, T.
2017.
On the motion of linked spheres in a Stokes flow.
Experiments in Fluids,
Vol. 58,
Issue. 4,
Vilfan, Mojca
Osterman, Natan
and
Vilfan, Andrej
2018.
Magnetically driven omnidirectional artificial microswimmers.
Soft Matter,
Vol. 14,
Issue. 17,
p.
3415.
Morita, Takeru
Omori, Toshihiro
and
Ishikawa, Takuji
2018.
Biaxial fluid oscillations can propel a microcapsule swimmer in an arbitrary direction.
Physical Review E,
Vol. 98,
Issue. 6,
Ishimoto, Kenta
and
Gaffney, Eamonn A.
2018.
Hydrodynamic Clustering of Human Sperm in Viscoelastic Fluids.
Scientific Reports,
Vol. 8,
Issue. 1,
Daddi-Moussa-Ider, Abdallah
Lisicki, Maciej
Mathijssen, Arnold J T M
Hoell, Christian
Goh, Segun
Bławzdziewicz, Jerzy
Menzel, Andreas M
and
Löwen, Hartmut
2018.
State diagram of a three-sphere microswimmer in a channel.
Journal of Physics: Condensed Matter,
Vol. 30,
Issue. 25,
p.
254004.
Morita, Takeru
Omori, Toshihiro
and
Ishikawa, Takuji
2018.
Passive swimming of a microcapsule in vertical fluid oscillation.
Physical Review E,
Vol. 98,
Issue. 2,
Kumar, Deepak
Sourav, Kumar
Yadav, Pavan Kumar
and
Sen, Subhankar
2019.
Understanding the secondary separation from an inclined square cylinder with sharp and rounded trailing edges.
Physics of Fluids,
Vol. 31,
Issue. 7,
Sharma, B.
and
Barman, R. N.
2020.
Steady laminar flow past a slotted circular cylinder.
Physics of Fluids,
Vol. 32,
Issue. 7,
Yu, Yang
Yang, Liuming
Gao, Yuan
and
Hou, Guoxiang
2021.
Lattice Boltzmann investigation of the influence of slip distributions on the flow past a diamond cylinder at low-Reynolds-number.
Physics of Fluids,
Vol. 33,
Issue. 7,
Berti, Luca
Chabannes, Vincent
Giraldi, Laetitia
and
Prud’homme, Christophe
2021.
Modelling and finite element simulation of multi-sphere swimmers.
Comptes Rendus. Mathématique,
Vol. 359,
Issue. 9,
p.
1119.
Berdakin, Ivan
Marconi, V. I.
and
Banchio, Adolfo J.
2022.
Boosting micromachine studies with Stokesian dynamics.
Physics of Fluids,
Vol. 34,
Issue. 3,
Chen, Qiaodan
Duan, Jun
Hou, Zhongbao
Hou, Guoxiang
and
Deng, Leimin
2022.
Effect of the surface pattern on the drag property of the superhydrophobic surface.
Physics of Fluids,
Vol. 34,
Issue. 11,
Vladimirov, V. A.
2022.
Distinguished limits and drifts: between nonuniqueness and universality.
Annales mathématiques du Québec,
Vol. 46,
Issue. 1,
p.
77.
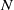 $N$-sphere micro-robot
$N$-sphere micro-robot $N$ spheres moving along a fixed line. The spheres are linked to each other by arms with their lengths changing periodically. We use the asymptotic procedure containing the two-timing method and a distinguished limit. We show that self-propulsion velocity appears (in the main approximation) as a linear combination of velocities of all possible triplets of spheres. Velocities and efficiencies of three-, four- and five-sphere swimmers are calculated.
$N$ spheres moving along a fixed line. The spheres are linked to each other by arms with their lengths changing periodically. We use the asymptotic procedure containing the two-timing method and a distinguished limit. We show that self-propulsion velocity appears (in the main approximation) as a linear combination of velocities of all possible triplets of spheres. Velocities and efficiencies of three-, four- and five-sphere swimmers are calculated.