Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T11:54:22.390Z Has data issue: false hasContentIssue false
  • English
  • Français

On the scaling of propagation of periodically generated vortex rings

Published online by Cambridge University Press:  22 August 2018

H. Asadi ,
H. Asgharzadeh  and
I. Borazjani Open the ORCID record for I. Borazjani [Opens in a new window]
H. Asadi
Affiliation:
Department of Mechanical Engineering, Texas A & M University, College Station, TX 77843, USA
H. Asgharzadeh
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, The State University of New York, Buffalo, NY 14260, USA
I. Borazjani*
Affiliation:
Department of Mechanical Engineering, Texas A & M University, College Station, TX 77843, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The propagation of periodically generated vortex rings (period 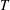$T$) is numerically investigated by imposing pulsed jets of velocity 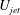$U_{jet}$ and duration 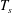$T_{s}$ (no flow between pulses) at the inlet of a cylinder of diameter 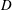$D$ exiting into a tank. Because of the step-like nature of pulsed jet waveforms, the average jet velocity during a cycle is 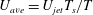$U_{ave}=U_{jet}T_{s}/T$. By using 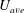$U_{ave}$ in the definition of the Reynolds number (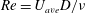$Re=U_{ave}D/\unicode[STIX]{x1D708}$, $\unicode[STIX]{x1D708}$: kinematic viscosity of fluid) and non-dimensional period (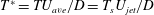$T^{\ast }=TU_{ave}/D=T_{s}U_{jet}/D$, i.e. equivalent to formation time), then based on the results, the vortex ring velocity 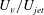$U_{v}/U_{jet}$ becomes approximately independent of the stroke ratio 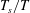$T_{s}/T$. The results also show that 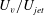$U_{v}/U_{jet}$ increases by reducing 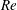$Re$ or increasing 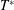$T^{\ast }$ (more sensitive to 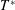$T^{\ast }$) according to a power law of the form 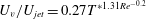$U_{v}/U_{jet}=0.27T^{\ast 1.31Re^{-0.2}}$. An empirical relation, therefore, for the location of vortex ring core centres (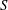$S$) over time ($t$) is proposed (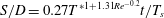$S/D=0.27T^{\ast 1+1.31Re^{-0.2}}t/T_{s}$), which collapses (scales) not only our results but also the results of experiments for non-periodic rings. This might be due to the fact that the quasi-steady vortex ring velocity was found to have a maximum of 15 % difference with the initial (isolated) one. Visualizing the rings during the periodic state shows that at low 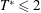$T^{\ast }\leqslant 2$ and high 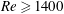$Re\geqslant 1400$ here, the stopping vortices become unstable and form hairpin vortices around the leading ones. However, by increasing 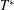$T^{\ast }$ or decreasing 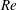$Re$ the stopping vortices remain circular. Furthermore, rings with short 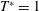$T^{\ast }=1$ show vortex pairing after approximately one period in the downstream, but higher 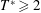$T^{\ast }\geqslant 2$ generates a train of vortices in the quasi-steady state.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 150 - 170
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. J. & Auvity, B. 2002 Interaction of a vortex ring with a piston vortex. J. Fluid Mech. 465, 353–378.Google Scholar
Anderson, A. B. C. 1955 Structure and velocity of the periodic vortex-ring pattern of a primary pfeifenton (pipe tone) jet. J. Acoust. Soc. Am. 27, 1048–1053.Google Scholar
Asgharzadeh, H. & Borazjani, I.2016 Effects of reynolds and womersley numbers on the hemodynamics of intracranial aneurysms, Comput. Math. Methods Med. 7412926, 2016.Google Scholar
Asgharzadeh, H. & Borazjani, I. 2017 A Newton–Krylov method with an approximate analytical Jacobian for implicit solution of Navier–Stokes equations on staggered overset-curvilinear grids with immersed boundaries. J. Comput. Phys. 331, 227–256.Google Scholar
Aydemir, E., Worth, N. A. & Dawson, J. R. 2012 The formation of vortex rings in a strongly forced jet. Exp. Fluids 52, 729–742.Google Scholar
Baird, M. H. I. 1977 Velocity and momentum of vortex rings in relation to formation parameters. Can. J. Chem. Engng 55, 19–26.Google Scholar
Borazjani, I. 2013 Fluid-structure interaction, immersed boundary-finite element method simulations of bio-prosthetic heart valves. Comput. Meth. Appl. Mech. Engng 257 (0), 103–116.Google Scholar
Borazjani, I. & Daghooghi, M. 2013 The fish tail motion forms an attached leading edge vortex. Proc. R. Soc. Lond. B 280 (1756), 20122071.Google Scholar
Borazjani, I., Ge, L., Le, T. & Sotiropoulos, F. 2013 A parallel overset-curvilinear-immersed boundary framework for simulating complex 3d incompressible flows. Comput. Fluids 77, 76–96.Google Scholar
Borazjani, I., Ge, L. & Sotiropoulos, F. 2008 Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3d rigid bodies. J. Comput. Phys. 227, 7587–7620.Google Scholar
Bottom, R. G., Borazjani, I., Blevins, E. L. & Lauder, G. V. 2016 Hydrodynamics of swimming in stingrays: numerical simulations and the role of the leading-edge vortex. J. Fluid Mech. 788, 407–443.Google Scholar
Burgers, J. M. 1948 A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199.Google Scholar
Colin, S. P. & Costello, J. H. 2002 Morphology, swimming performance and propulsive mode of six co-occuring hydromedusae. J. Expl Biol. 205, 427–437.Google Scholar
Dabiri, J. O., Colin, S. P., Costello, J. H. & Gharib, M. 2005 Flow patterns generated by oblate medusan jellyfish: field measurements and laboratory analysis. J. Expl Biol. 208, 1257–1265.Google Scholar
Daghooghi, M. & Borazjani, I. 2015a The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomim. 10 (5), 056018.Google Scholar
Daghooghi, M. & Borazjani, I. 2015b The influence of inertia on the rheology of a periodic suspension of neutrally buoyant rigid ellipsoids. J. Fluid Mech. 781, 506–549.Google Scholar
Davidson, P. 2015 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Devore, J. L. 2011 Probability and Statistics for Engineering and the Sciences, 8th edn, pp. 508–510. Boston, MA, Cengage Learning, ISBN 0-538-73352-7.Google Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30, 101–116.Google Scholar
Fukumoto, Y. & Moffatt, H. K. 2000 Motion and expansion of a viscous vortex ring. Part 1. A higher-order asymptotic formula for the velocity. J. Fluid Mech. 417, 1–45.Google Scholar
Gan, L. & Nickels, T. B. 2010 An experimental study of turbulent vortex rings during their early development. J. Fluid Mech. 649, 467–496.Google Scholar
Ge, L. & Sotiropoulos, F. 2007 A numerical method for solving the 3d unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 225, 1782–1809.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.Google Scholar
Gilmanov, A. & Sotiropoulos, F. 2005 A hybrid Cartesian/immersed boundary method for simulating flows with 3d, geometrically complex, moving bodies. J. Comput. Phys. 207, 457–492.Google Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532–3542.Google Scholar
Gopalakrishnan, S. S., Pier, B. & Biesheuvel, A. 2014 Dynamics of pulsatile flow through model abdominal aorotic aneurysms. J. Fluid Mech. 758, 150–179.Google Scholar
Jahanbakhshi, R., Vaghefi, N. S. & Madnia, C. K. 2015 Baroclinic vorticity generation near the turbulent/non-turbulent interface in a compressible shear layer. Phys. Fluids 27, 105105.Google Scholar
James, S. & Madnia, C. K. 1996 Direct numerical simulation of a laminar vortex ring. Phys. Fluids 8 (9), 2400–2414.Google Scholar
Kheradvar, A., Houle, H., Pedrizzetti, G., Tonti, G., Belcik, T., Ashraf, M., Lindner, J. R., Gharib, M. & Sahn, D. 2010 Echocardiographic particle image velocimetry: a novel technique for quantification of left ventricle blood vorticity pattern. J. Am. Soc. Echocardiography 23, 86–94.Google Scholar
Krieg, M. & Mohseni, K. 2008 Thrust characterization of a bioinspired vortex ring thruster for locomotion of underwater robots. IEEE J. Ocean. Engng 33, 123–132.Google Scholar
Krieg, M. & Mohseni, K. 2015 Pressure and work analysis of unsteady, deformable, axisymmetric, jet producing cavity bodies. J. Fluid Mech. 769, 337–368.Google Scholar
Krueger, P. S. 2010 Vortex ring velocity and minimum separation in an infinite train of vortex rings generated by a fully pulsed jet. Theor. Comput. Fluid Dyn. 24, 291–297.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lawson, J. M. & Dawson, J. R. 2013 The formation of turbulent vortex rings by synthetic jets. Phys. Fluids 25 (10), 105113.Google Scholar
Le, T. B., Borazjani, I., Kang, S. & Sotiropoulos, F. 2011 On the structure of vortex rings from inclined nozzles. J. Fluid Mech. 686, 451–483.Google Scholar
Le, T. B., Borazjani, I. & Sotiropoulos, F. 2010 Pulsatile flow effects on the hemodynamics of intracranial aneurysms. J. Biomech. Engng 132, 111009.Google Scholar
Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51 (1), 15–32.Google Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81 (3), 465–495.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35 (1), 117–129.Google Scholar
Mohseni, K. 2006 A formulation for calculating the translational velocity of a vortex ring or pair. Bioinspir. Biomim. 1 (4), S57–S64.Google Scholar
Nitsche, M. & Krasny, R. 1994 A numerical study of vortex ring formation at the edge of a circular tube. J. Fluid Mech. 276, 139–161.Google Scholar
Saffman, P. G. 1978 The number of waves on unstable vortex rings. J. Fluid Mech. 84 (4), 625–639.Google Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49, 371–380.Google Scholar
Salsac, A.-V., Sparks, S. R., Chomaz, J.-M. & Lasheras, J. C. 2006 Evolution of the wall sheear stresses during the progressive enlargments of symmetric abdominal aortic aneurysms. J. Fluid Mech. 560, 19–51.Google Scholar
Schlueter-Kuck, K. & Dabiri, J. O. 2016 Pressure evolution in the shear layer of forming vortex rings. Phys. Rev. Fluids 1 (1), 012501.Google Scholar
Schram, C. & Riethmuller, M. L. 2002 Measurement of vortex ring characteristics during pairing in a forced subsonic air jet. Exp. Fluids 33, 879–888.Google Scholar
Sullivan, I., Niemela, J. J., Hershberger, R. E., Bolster, D. & Donnelly, R. J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319–347.Google Scholar
Taveira, R. R., Diogo, J. S., Lopes, D. C. & da Silva, C. B. 2013 Lagrangian statistics across the turbulent-nonturbulent interface in a turbulent plane jet. Phys. Rev. E 88 (4), 043001.Google Scholar
Webster, D. R. & Longmire, E. K. 1998 Vortex rings from cylinders with inclined exits. Phys. Fluids 10, 400–416.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1980 Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 101 (3), 449–491.Google Scholar

Asadi et al. supplementary movie 1

The isosurface of vorticity magnitude colored by helicity starting from rest (t=0) to quasi-steady state for case 3 (Re=1400, T*=1). Link in the text: Movie 1

Download Asadi et al. supplementary movie 1(Video)
Video 26.9 MB

Asadi et al. supplementary movie 2

Out-of-plane vorticity for case 3 (Re=1400, T*=1) contours starting from rest (t=0) to quasi-steady state. Link in the text: Movie 2

Download Asadi et al. supplementary movie 2(Video)
Video 4.2 MB

Asadi et al. supplementary movie 3

Out-of-plane vorticity on the midplane for case 3 (Re=1400, T*=1) contours during quasi-steady state. Link in the text: Movie 3

Download Asadi et al. supplementary movie 3(Video)
Video 1 MB

Asadi et al. supplementary movie 4

Out-of-plane vorticity on the midplane for case 4 (Re=1400, T*=2) contours during quasi-steady state. Link in the text: Movie 4

Download Asadi et al. supplementary movie 4(Video)
Video 2.7 MB

Asadi et al. supplementary movie 5

Out-of-plane vorticity on the midplane for case 5 (Re=11,500, T*=1) contours during quasi-steady state. Link in the text: Movie 5

Download Asadi et al. supplementary movie 5(Video)
Video 5.5 MB

Asadi et al. supplementary movie 6

Out-of-plane vorticity on the midplane for case 6 (Re=11,500, T*=2) contours during quasi-steady state. Link in the text: Movie 6

Download Asadi et al. supplementary movie 6(Video)
Video 3.9 MB

Asadi et al. supplementary movie 7

The isosurface of Q-criteria for case 6 (Re=11,500, T*=2) from rest (t=0) to quasi-steady state. Link in the text: Movie 7

Download Asadi et al. supplementary movie 7(Video)
Video 4.7 MB

Asadi et al. supplementary movie 8

The isosurface of Q-criteria for case 5 (Re=11,500, T*=1) from rest (t=0) to quasi-steady state. Link in the text: Movie 8

Download Asadi et al. supplementary movie 8(Video)
Video 3.3 MB