Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T16:06:31.047Z Has data issue: false hasContentIssue false
  • English
  • Français

On fluid motion in librating ellipsoids with moderate equatorial eccentricity

Published online by Cambridge University Press:  15 March 2011

KEKE ZHANG ,
KIT H. CHAN  and
XINHAO LIAO
KEKE ZHANG*
Affiliation:
Department of Mathematical Sciences, University of Exeter, Exeter EX4 4QF, UK
KIT H. CHAN
Affiliation:
Department of Mathematics, University of Hong Kong, Pokfulam, Hong Kong
XINHAO LIAO
Affiliation:
Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

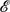The motion of a homogeneous fluid of viscosity ν confined in a librating ellipsoidal cavity with semi-axes a and moderate equatorial eccentricity is investigated. The ellipsoid rotates with an angular velocity Ω0(1 + δsin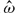t), where Ω0 is the mean rate of rotation, 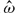is the libration frequency and Ω0δ represents the amplitude of longitudinal libration. When δ ≪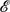2 and E1/2 ≪ 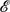2 ≪ 1, where E is the Ekman number defined as E = ν/(a2Ω0), an explicit analytical solution describing fluid motion in librating ellipsoids is derived for any size of the libration frequency 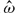. Three-dimensional numerical simulations of the same problem are also performed, revealing the generation of mean zonal flow in librating ellipsoidal cavities and showing a satisfactory agreement between the asymptotic and numerical analyses.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 673 , 25 April 2011 , pp. 468 - 479
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37, 307–323.CrossRefGoogle Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.CrossRefGoogle Scholar
Calkins, M. A., Noir, J., Eldredge, J. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602.CrossRefGoogle Scholar
Dermott, S. F. 1979 Shapes and gravitational moments of satellites and asteroids. Icarus 37, 576–586.CrossRefGoogle Scholar
Margot, J. L., Peale, S. J., Jurgens., R. F., Slade, M. A. & Holin, I. V. 2007 Large longitude libration of mercury reveals a molten core. Science 316, 710–714.CrossRefGoogle ScholarPubMed
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173, 141–152.CrossRefGoogle Scholar
Rieutord, M. 1991 Linear theory of rotating fluids using spherical harmonics. Part II. Time-periodic flows. Geophys. Astrophys. Fluid Dyn. 59, 185–208CrossRefGoogle Scholar
Sauret, A., Cebron, D., Morize, C. & LeBars, M. Bars, M. 2010 Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662, 260–268.CrossRefGoogle Scholar
Tilgner, A. 1999. Driven inertial oscillations in spherical shells. Phys. Rev. E 59, 1789–1794.CrossRefGoogle Scholar
William, J. G., Boggs, D. H., Yoder, C. F., Ratcliiff, J. T. & Dickey, J. O. 2001 Lunar rotational dissipation in solid body and molten core. J. Geophys. Res. 106, 27933–27968.CrossRefGoogle Scholar
Zhang, K., Earnshaw, P., Liao, X. & Busse, F. H. 2001 On inertial waves in a rotating fluid sphere. J. Fluid Mech. 437, 103–119.CrossRefGoogle Scholar
Zhang, K., Chan, K. & Liao, X. 2010 On fluid flows in precessing spheres in the mantle frame of reference. Phys. Fluid 22, 116604.CrossRefGoogle Scholar