Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T16:49:25.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical simulations of the agitation generated by coarse-grained bubbles moving at large Reynolds number

Published online by Cambridge University Press:  07 September 2021

F. Le Roy De Bonneville Open the ORCID record for F. Le Roy De Bonneville [Opens in a new window] ,
R. Zamansky Open the ORCID record for R. Zamansky [Opens in a new window] ,
F. Risso Open the ORCID record for F. Risso [Opens in a new window] ,
A. Boulin  and
J.-F. Haquet
F. Le Roy De Bonneville
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France SMTA, LMAG, CEA, DEN, DTN, 13108Saint-Paul-Lez-Durance, France
R. Zamansky*
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
F. Risso
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
A. Boulin
Affiliation:
SMTA, LMAG, CEA, DEN, DTN, 13108Saint-Paul-Lez-Durance, France
J.-F. Haquet
Affiliation:
SMTA, LMAG, CEA, DEN, DTN, 13108Saint-Paul-Lez-Durance, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

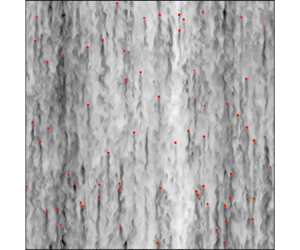
We present a numerical method for simulating the flow induced by bubbles rising at large Reynolds number. This method is useful to simulate configurations of large dimensions involving a great number of bubbles. The action that each bubble exerts on the liquid is modelled as a volume source of momentum distributed over a few mesh-grid elements. The flow in the vicinity of the bubbles is thus not finely resolved. The bubbles are treated as Lagrangian particles that move under the influence of the hydrodynamic force exerted by the liquid. The determination of this force on a given bubble requires knowledge of the liquid flow that is undisturbed by this bubble. A model is developed to accurately estimate this disturbance for large-Reynolds-number objects and get rid of any spurious self-induced effect. Thanks to that, a homogeneous swarm of rising bubbles is simulated. Comparisons with experiments show a good agreement with the flow scales larger than the bubbles, which turn out to be controlled by the interactions between bubble wakes and rather independent of unresolved smaller scales. This method can be used to study the coupling between bubble-induced agitation and large-scale motions, such as those produced in industrial bubble columns.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Gas/liquid flow Turbulent Flows: Homogeneous turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 926 , 10 November 2021 , A20
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akiki, G., Jackson, T.L. & Balachandar, S. 2017 Pairwise interaction extended point-particle model for a random array of monodisperse spheres. J. Fluid Mech. 813, 882–928.CrossRefGoogle Scholar
Alméras, E., Mathai, V., Lohse, D. & Sun, C. 2017 Experimental investigation of the turbulence induced by a bubble swarm rising within incident turbulence. J. Fluid Mech. 825, 1091–1112.CrossRefGoogle Scholar
Alméras, E., Plais, C., Euzenat, F., Risso, F., Roig, V. & Augier, F. 2016 Scalar mixing in bubbly flows: experimental investigation and diffusivity modelling. Chem. Engng Sci. 140, 114–122.CrossRefGoogle Scholar
Amoura, Z., Besnaci, C., Risso, F. & Roig, V. 2017 Velocity fluctuations generated by the flow through a random array of spheres: a model of bubble-induced agitation. J. Fluid Mech. 823, 592–616.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J.K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Balachandar, S., Liu, K. & Lakhote, M. 2019 Self-induced velocity correction for improved drag estimation in Euler–Lagrange point-particle simulations. J. Comput. Phys. 376, 160–185.CrossRefGoogle Scholar
Boivin, M., Simonin, O. & Squires, K.D. 1998 Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375, 235–263.CrossRefGoogle Scholar
Bos, W.J.T. & Zamansky, R. 2019 Power fluctuations in turbulence. Phys. Rev. Lett. 122 (12), 124504.CrossRefGoogle ScholarPubMed
Canuto, C., Hussaini, M.Y., Quarteroni, A. & Zang, T.A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Capecelatro, J. & Desjardins, O. 2013 An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys. 238, 1–31.CrossRefGoogle Scholar
Climent, E. & Magnaudet, J. 1999 Large-scale simulations of bubble-induced convection in a liquid layer. Phys. Rev. Lett. 82 (24), 4827–4830.CrossRefGoogle Scholar
Colombet, D., Legendre, D., Risso, F., Cockx, A. & Guiraud, P. 2015 Dynamics and mass transfer of rising bubbles in a homogenous swarm at large gas volume fraction. J. Fluid Mech. 763, 254–285.CrossRefGoogle Scholar
Du Cluzeau, A. 2019 Modélisation physique de la dynamique des écoulements à bulles par remontée d’échelle à partir de simulations fines. Theses, Université de Perpignan.Google Scholar
du Cluzeau, A., Bois, G. & Toutant, A. 2019 Analysis and modelling of Reynolds stresses in turbulent bubbly up-flows from direct numerical simulations. J. Fluid Mech. 866, 132–168.CrossRefGoogle Scholar
du Cluzeau, A., Bois, G., Toutant, A. & Martinez, J.-M. 2020 On bubble forces in turbulent channel flows from direct numerical simulations. J. Fluid Mech. 882, A27.CrossRefGoogle Scholar
Elghobashi, S. 2018 DNS of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 43, 1–28.Google Scholar
Ellingsen, K. & Risso, F. 2001 On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity. J. Fluid Mech. 440, 235–268.CrossRefGoogle Scholar
Garnier, C., Lance, M. & Marié, J.L. 2002 Measurement of local flow characteristics in buoyancy-driven bubbly flow at high void fraction. Exp. Therm. Fluid Sci. 26 (6), 811–815.CrossRefGoogle Scholar
Gatignol, R. 1983 The Faxén formulae for a rigid particle in an unsteady non-uniform Stokes flow. J. Méc. Théor. Appl. 1, 143–160.Google Scholar
Gorokhovski, M. & Zamansky, R. 2018 Modeling the effects of small turbulent scales on the drag force for particles below and above the Kolmogorov scale. Phys. Rev. Fluids 3 (3), 034602.CrossRefGoogle Scholar
Gualtieri, P., Picano, F., Sardina, G. & Casciola, C.M. 2015 Exact regularized point particle method for multiphase flows in the two-way coupling regime. J. Fluid Mech. 773, 520–561.CrossRefGoogle Scholar
Gvozdić, B., Alméras, E., Mathai, V., Zhu, X., van Gils, D.P.M., Verzicco, R., Huisman, S.G., Sun, C. & Lohse, D. 2018 Experimental investigation of heat transport in homogeneous bubbly flow. J. Fluid Mech. 845, 226–244.CrossRefGoogle Scholar
Hallez, Y. & Legendre, D. 2011 Interaction between two spherical bubbles rising in a viscous liquid. J. Fluid Mech. 673 (1), 406–431.CrossRefGoogle Scholar
Harper, J.F. 1997 Bubbles rising in line: why is the first approximation so bad? J. Fluid Mech. 351, 289–300.CrossRefGoogle Scholar
Hasslberger, J., Klein, M. & Chakraborty, N. 2018 Flow topologies in bubble-induced turbulence: a direct numerical simulation analysis. J. Fluid Mech. 857, 270–290.CrossRefGoogle Scholar
Horwitz, J.A.K. & Mani, A. 2016 Accurate calculation of stokes drag for point–particle tracking in two-way coupled flows. J. Comput. Phys. 318, 85–109.CrossRefGoogle Scholar
Huck, P.D., Bateson, C., Volk, R., Cartellier, A., Bourgoin, M. & Aliseda, A. 2018 The role of collective effects on settling velocity enhancement for inertial particles in turbulence. J. Fluid Mech. 846, 1059–1075.CrossRefGoogle Scholar
Hunt, J.C.R & Eames, I 2002 The disappearance of laminar and turbulent wakes in complex flows. J. Fluid Mech. 457, 111–132.CrossRefGoogle Scholar
Ireland, P.J. & Desjardins, O. 2017 Improving particle drag predictions in Euler–Lagrange simulations with two-way coupling. J. Comput. Phys. 338, 405–430.CrossRefGoogle Scholar
Ishii, M. & Zuber, N. 1979 Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 25 (5), 843–855.CrossRefGoogle Scholar
Jackson, J.D. 1999 Classical Electrodynamics, 3rd edn. John Wiley & Sons.Google Scholar
Lai, C.C.K., Fraga, B., Chan, W.R.H. & Dodd, M.S. 2019 Energy cascade in a homogeneous swarm of bubbles rising in a vertical channel. In Proceedings of the Summer Program 2018. Center for Turbulence Research, Stanford University.Google Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 222, 95–118.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.M. 1975 Course of Theoretical Physics, 2, The Classical Theory of Fields, 4th edn. Butterworth-Heinemann.Google Scholar
Loisy, A. & Naso, A. 2017 Interaction between a large buoyant bubble and turbulence. Phys. Rev. Fluids 2, 014606.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.CrossRefGoogle Scholar
Martínez Mercado, J., Palacios-Morales, C.A. & Zenit, R. 2007 Measurement of pseudoturbulence intensity in monodispersed bubbly liquids for $10< Re<500$. Phys. Fluids 19 (10), 103302.CrossRefGoogle Scholar
Maxey, M. 2017 Simulation methods for particulate flows and concentrated suspensions. Annu. Rev. Fluid Mech. 49 (1), 171–193.CrossRefGoogle Scholar
Maxey, M.R., Patel, B.K., Chang, E.J. & Wang, L.P 1997 Simulations of dispersed turbulent multiphase flow. Fluid Dyn. Res. 20, 143–156.CrossRefGoogle Scholar
Maxey, M.R. & Riley, J.J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Maxworthy, T., Gnann, C., Kürten, M. & Durst, F. 1996 Experiments on the rise of air bubbles in clean viscous liquids. J. Fluid Mech. 321, 421–441.CrossRefGoogle Scholar
Mendez-Diaz, S., Serrano-García, J.C., Zenit, R. & Hernández-Cordero, J.A. 2013 Power spectral distributions of pseudo-turbulent bubbly flows. Phys. Fluids 25 (4), 043303.CrossRefGoogle Scholar
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Reynolds-number spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.CrossRefGoogle Scholar
Monin, A.S. & Yaglom, A.M. 1981 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2. MIT Press.Google Scholar
Moore, D.W. 1965 The velocity of rise of distorted gas bubbles in a liquid of small viscosity. J. Fluid Mech. 23 (4), 749–766.CrossRefGoogle Scholar
Morente, A., Laviéville, J. & Legendre, D. 2018 A penalization method for the simulation of bubbly flows. J. Comput. Phys. 374, 563–590.CrossRefGoogle Scholar
Mudde, R.F. 2005 Gravity-driven bubbly flows. Annu. Rev. Fluid Mech. 37 (1), 393–423.CrossRefGoogle Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12 (3), 033040.CrossRefGoogle Scholar
Onishi, R., Takahashi, K. & Vassilicos, J.C. 2013 An efficient parallel simulation of interacting inertial particles in homogeneous isotropic turbulence. J. Comput. Phys. 242, 809–827.CrossRefGoogle Scholar
Orszag, S.A. 1971 On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28 (6), 1074–1074.2.0.CO;2>CrossRefGoogle Scholar
Pandey, V., Ramadugu, R. & Perlekar, P. 2020 Liquid velocity fluctuations and energy spectra in three-dimensional buoyancy-driven bubbly flows. J. Fluid Mech. 884, R6.CrossRefGoogle Scholar
Pekurovsky, D. 2012 P3dfft: a framework for parallel computations of fourier transforms in three dimensions. SIAM J. Sci. Comput. 34 (4), C192–C209.CrossRefGoogle Scholar
Prakash, V.N., Martínez Mercado, J., van Wijngaarden, L., Mancilla, E., Tagawa, Y., Lohse, D. & Sun, C. 2016 Energy spectra in turbulent bubbly flows. J. Fluid Mech. 791, 174–190.CrossRefGoogle Scholar
Rawat, S., Chouippe, A., Zamansky, R., Legendre, D. & Climent, E. 2018 Drag modulation in turbulent boundary layers subject to different bubble injection strategies. Comput. Fluids 178, 73–87.CrossRefGoogle Scholar
Rensen, J., Luther, S. & Lohse, D. 2005 The effect of bubbles on developed turbulence. J. Fluid Mech. 538, 153–187.CrossRefGoogle Scholar
Riboux, G, Legendre, D & Risso, F. 2013 A model of bubble-induced turbulence based on large-scale wake interactions. J. Fluid Mech. 719, 362–387.CrossRefGoogle Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.CrossRefGoogle Scholar
Risso, F. 2016 Physical interpretation of probability density functions of bubble-induced agitation. J. Fluid Mech. 809, 240–263.CrossRefGoogle Scholar
Risso, F. 2018 Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50 (1), 25–48.CrossRefGoogle Scholar
Risso, F. & Ellingsen, K. 2002 Velocity fluctuations in a homogeneous dilute dispersion of high-Reynolds-number rising bubbles. J. Fluid Mech. 453, 395–410.CrossRefGoogle Scholar
Risso, F., Roig, V., Amoura, Z., Riboux, G. & Billet, A.-M. 2008 Wake attenuation in large Reynolds number dispersed two-phase flows. Phil. Trans. A 366 (1873), 2177–2190.CrossRefGoogle ScholarPubMed
Saffman, P.G. 1973 On the settling speed of free and fixed suspensions. Stud. Appl. Maths 52 (2), 115–127.CrossRefGoogle Scholar
Sangani, A.S. & Didwania, A.K. 2006 Dynamic simulations of flows of bubbly liquids at large Reynolds numbers. J. Fluid Mech. 250, 307–337.CrossRefGoogle Scholar
Subramaniam, S. 2013 Lagrangian–Eulerian methods for multiphase flows. Prog. Energy Combust. Sci. 39 (2), 215–245.CrossRefGoogle Scholar
Subramaniam, S., Mehrabadi, M., Horwitz, J. & Mani, A. 2014 Developing improved lagrangian point particle models of gas-solid flow from particle-resolved direct numerical simulation. In Proceedings of the Summer Program 2014. Center for Turbulence Research - Stanford University.Google Scholar
Tenneti, S. & Subramaniam, S. 2014 Particle-resolved direct numerical simulation for gas-solid flow model development. Annu. Rev. Fluid Mech. 46, 199–230.CrossRefGoogle Scholar
Uhlmann, M. & Chouippe, A. 2017 Clustering and preferential concentration of finite-size particles in forced homogeneous-isotropic turbulence. J. Fluid Mech. 812, 991–1023.CrossRefGoogle Scholar
van Wijngaarden, L. 1993 The mean rise velocity of pairwise-interacting bubbles in liquid. J. Fluid Mech. 251, 55–78.CrossRefGoogle Scholar
van Wijngaarden, L. 2005 Bubble velocities induced by trailing vortices behind neighbours. J. Fluid Mech. 541, 203–229.CrossRefGoogle Scholar
Xu, Y. & Subramaniam, S. 2007 Consistent modeling of interphase turbulent kinetic energy transfer in particle-laden turbulent flows. Phys. Fluids 19 (8), 085101.CrossRefGoogle Scholar
Yeung, P.K. & Pope, S.B. 1988 An algorithm for tracking fluid particles in numerical simulations of homogeneous turbulent. J. Comput. Phys. 79, 373–416.CrossRefGoogle Scholar
Yurkovetsky, Y. & Brady, J.F. 1996 Statistical mechanics of bubbly liquids. Phys. Fluids 8 (4), 881–895.CrossRefGoogle Scholar
Zamansky, R., Coletti, F., Massot, M. & Mani, A. 2016 Turbulent thermal convection driven by heated inertial particles. J. Fluid Mech. 809, 390–437.CrossRefGoogle Scholar
Zenit, R., Koch, D.L. & Sangani, A.S. 2001 Measurements of the average properties of a suspension of bubbles rising in a vertical channel. J. Fluid Mech. 429, 307–342.CrossRefGoogle Scholar
Zenit, R. & Magnaudet, J. 2008 Path instability of rising spheroidal air bubbles: a shape-controlled process. Phys. Fluids 20 (6), 061702.CrossRefGoogle Scholar
Zhang, Z., Legendre, D. & Zamansky, R. 2019 Model for the dynamics of micro-bubbles in high Reynolds number flows. J. Fluid Mech. 879, 554–578.CrossRefGoogle Scholar