Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sharaf, Omar Z.
Taylor, Robert A.
and
Abu-Nada, Eiyad
2020.
On the colloidal and chemical stability of solar nanofluids: From nanoscale interactions to recent advances.
Physics Reports,
Vol. 867,
Issue. ,
p.
1.
Zeidan, D.
Zhang, L. T.
and
Goncalves, E.
2020.
High-Resolution Simulations for Aerogel Using Two-Phase Flow Equations and Godunov Methods.
International Journal of Applied Mechanics,
Vol. 12,
Issue. 05,
p.
2050049.
Peng, Zhengbiao
Doroodchi, Elham
and
Moghtaderi, Behdad
2020.
Heat transfer modelling in Discrete Element Method (DEM)-based simulations of thermal processes: Theory and model development.
Progress in Energy and Combustion Science,
Vol. 79,
Issue. ,
p.
100847.
Mohammadpour, Javad
Lee, Ann
Mozafari, M.
Zargarabadi, Mehran Rajabi
and
Mujumdar, Arun S.
2021.
Evaluation of Al2O3-Water nanofluid in a microchannel equipped with a synthetic jet using single-phase and Eulerian–Lagrangian models.
International Journal of Thermal Sciences,
Vol. 161,
Issue. ,
p.
106705.
Sankar, M.
Reddy, N. Keerthi
and
Do, Younghae
2021.
Conjugate buoyant convective transport of nanofluids in an enclosed annular geometry.
Scientific Reports,
Vol. 11,
Issue. 1,
Tibaut, J.
Tibaut, T.
and
Ravnik, J.
2021.
Numerical simulation of mixed convection of a nanofluid in a circular pipe with different numerical models.
Journal of Thermal Analysis and Calorimetry,
Vol. 145,
Issue. 5,
p.
2525.
Sharaf, Omar Z.
Rizk, Nahla
Munro, Catherine J.
Joshi, Chakra P.
Anjum, Dalaver H.
Abu-Nada, Eiyad
Martin, Matthew N.
and
Alazzam, Anas
2021.
Radiation stability and photothermal performance of surface-functionalized plasmonic nanofluids for direct-absorption solar applications.
Solar Energy Materials and Solar Cells,
Vol. 227,
Issue. ,
p.
111115.
Akram, Naveed
Montazer, Elham
Kazi, S.N.
Soudagar, Manzoore Elahi M.
Ahmed, Waqar
Zubir, Mohd Nashrul Mohd
Afzal, Asif
Muhammad, Mohd Ridha
Ali, Hafiz Muhammad
Márquez, Fausto Pedro García
and
Sarsam, Wail Sami
2021.
Experimental investigations of the performance of a flat-plate solar collector using carbon and metal oxides based nanofluids.
Energy,
Vol. 227,
Issue. ,
p.
120452.
Mohammadpour, Javad
Salehi, Fatemeh
Sheikholeslami, Mohsen
Masoudi, Mojtaba
and
Lee, Ann
2021.
Optimization of nanofluid heat transfer in a microchannel heat sink with multiple synthetic jets based on CFD-DPM and MLA.
International Journal of Thermal Sciences,
Vol. 167,
Issue. ,
p.
107008.
Amidu, Muritala Alade
Addad, Yacine
Riahi, Mohamed Kamel
and
Abu-Nada, Eiyad
2021.
Numerical investigation of nanoparticles slip mechanisms impact on the natural convection heat transfer characteristics of nanofluids in an enclosure.
Scientific Reports,
Vol. 11,
Issue. 1,
Rostami, Javad
2021.
Convective heat transfer by micro-encapsulated PCM in a mini-duct.
International Journal of Thermal Sciences,
Vol. 161,
Issue. ,
p.
106737.
Shan, Jie
and
Zhou, Xiaojun
2021.
The Effect of Bubbles on Particle Migration in Non-Newtonian Fluids.
Separations,
Vol. 8,
Issue. 4,
p.
36.
Han, Qi
Zhou, Xian-Tai
He, Xiao-Qi
and
Ji, Hong-Bing
2021.
Mechanism and kinetics of the aerobic oxidation of benzyl alcohol to benzaldehyde catalyzed by cobalt porphyrin in a membrane microchannel reactor.
Chemical Engineering Science,
Vol. 245,
Issue. ,
p.
116847.
Kannan, Ananda Subramani
Mark, Andreas
Maggiolo, Dario
Sardina, Gaetano
Sasic, Srdjan
and
Ström, Henrik
2021.
Assessment of hindered diffusion in arbitrary geometries using a multiphase DNS framework.
Chemical Engineering Science,
Vol. 230,
Issue. ,
p.
116074.
Somasundaram, Rajamani
and
Subramanyam Reddy, Anala
2021.
Pulsating flow of electrically conducting couple stress nanofluid in a channel with ohmic dissipation and thermal radiation – Dynamics of blood.
Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering,
Vol. 235,
Issue. 6,
p.
1895.
Sharaf, Omar Z.
Rizk, Nahla
Munro, Catherine J.
Joshi, Chakra P.
Waheed, Waqas
Abu-Nada, Eiyad
Alazzam, Anas
and
Martin, Matthew N.
2021.
Thermal stability and plasmonic photothermal conversion of surface-modified solar nanofluids: Comparing prolonged and cyclic thermal treatments.
Energy Conversion and Management,
Vol. 244,
Issue. ,
p.
114463.
Said, Zafar
Sundar, L. Syam
Tiwari, Arun Kumar
Ali, Hafiz Muhammad
Sheikholeslami, Mohsen
Bellos, Evangelos
and
Babar, Hamza
2022.
Recent advances on the fundamental physical phenomena behind stability, dynamic motion, thermophysical properties, heat transport, applications, and challenges of nanofluids.
Physics Reports,
Vol. 946,
Issue. ,
p.
1.
Goswami, Krishno D.
Chattopadhyay, Anirban
Pandit, Swapan K.
and
Sheremet, Mikhail A.
2022.
Transient thermogravitational convection for magneto hybrid nanofluid in a deep cavity with multiple isothermal source-sink pairs.
International Journal of Thermal Sciences,
Vol. 173,
Issue. ,
p.
107376.
Hussain, Muzamil
Shah, Syed Khawar Hussain
Sajjad, Uzair
Abbas, Naseem
and
Ali, Ahsan
2022.
Recent Developments in Optical and Thermal Performance of Direct Absorption Solar Collectors.
Energies,
Vol. 15,
Issue. 19,
p.
7101.
Hindebu, Bullo
Makinde, O. D.
and
Guta, Lemi
2022.
Unsteady mixed convection flow of variable viscosity nanofluid in a micro-channel filled with a porous medium.
Indian Journal of Physics,
Vol. 96,
Issue. 6,
p.
1749.
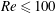 $Re\leqslant 100$). Momentum and thermal interactions between fluid and particle phases were accounted for using a transient two-way coupling algorithm implemented within an in-house code that tracked the simultaneous evolution of the carrier and particulate phases while considering timescale differences between the two phases. The inaccuracy of assuming a homogeneous particle distribution in modelling nanofluid flow in microchannels was established. In particular, shear rate and thermophoresis were found to play a key role in the lateral migration of nanoparticles and in the formation of particle depletion and accumulation regions in the vicinity of the channel walls. At low Reynolds numbers, nanoparticle distribution near the walls was observed to gradually flatten in the streamwise direction. On the other hand, for relatively higher Reynolds numbers, higher particle non-uniformities were observed in the vicinity of the channel walls. Furthermore, it was established that convective heat transfer between channel walls and the bulk fluid can either improve or deteriorate with the addition of nanoparticles, depending on whether the flow exceeded a critical Reynolds number of enhancement. It was also established that Brownian motion and thermophoresis had a major role in nanoparticle deposition on the channel walls. In particular, Brownian motion was the main deposition mechanism for nano-sized particles, whereas due to thermophoresis, nanoparticles were repelled away from channel walls. The result of the competition between the two is that deposition gradually increased along the streamwise direction.
$Re\leqslant 100$). Momentum and thermal interactions between fluid and particle phases were accounted for using a transient two-way coupling algorithm implemented within an in-house code that tracked the simultaneous evolution of the carrier and particulate phases while considering timescale differences between the two phases. The inaccuracy of assuming a homogeneous particle distribution in modelling nanofluid flow in microchannels was established. In particular, shear rate and thermophoresis were found to play a key role in the lateral migration of nanoparticles and in the formation of particle depletion and accumulation regions in the vicinity of the channel walls. At low Reynolds numbers, nanoparticle distribution near the walls was observed to gradually flatten in the streamwise direction. On the other hand, for relatively higher Reynolds numbers, higher particle non-uniformities were observed in the vicinity of the channel walls. Furthermore, it was established that convective heat transfer between channel walls and the bulk fluid can either improve or deteriorate with the addition of nanoparticles, depending on whether the flow exceeded a critical Reynolds number of enhancement. It was also established that Brownian motion and thermophoresis had a major role in nanoparticle deposition on the channel walls. In particular, Brownian motion was the main deposition mechanism for nano-sized particles, whereas due to thermophoresis, nanoparticles were repelled away from channel walls. The result of the competition between the two is that deposition gradually increased along the streamwise direction.

